2. Основы теории графов

2.1. Введение в теорию графов

Под абстрактным графом подразумевают математический объект в виде совокупности множества точек и множества линий между ними. Граф можно рассматривать как один из способов представления бинарных отношений. Множество линий, попарно соединяющих точки , представляют отображение множества самого в себя. Соответственно график отношения есть множество пар или кортежей вида . Следовательно, граф может быть задан парой множеств и :

Геометрически граф изображается в виде множества точек или кружков на плоскости называемых вершинами, и линий со стрелками (дуг), соединяющих пары вершин, между которыми установлено отношение . Если находится в отношении к , то стрелка дуги направлена от к . При этом в общем случае ( - образ элемента ). На рисунке 2.1 приведены графы, изображающие отношения, рассмотренные в примерах 1.15 и 1.16.

С помощью графов наглядно представляются отношения между элементами множеств. В качестве примера рассмотрим отношения между кодовыми комбинациями множества с точки зрения свойства, называемого пересечением. Считается, что n–разрядная кодовая комбинация пересекается с другой, если (n-1) последних ее элементов совпадают с (n-1) первыми элементами другой. Следовательно, график должен задавать отображение каждой кодовой комбинации, с которыми она пересекается. Обозначив элементы множества через с порядковыми номерами, устанавливаем, что комбинация пересекается сама с собой и с комбинацией , то есть . Аналогично для находим , для комбинации - и, наконец, для - . 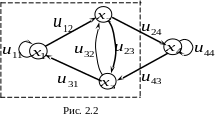Граф, отображающий свойство пересечения для двухразрядных двоичных кодовых комбинаций, представлен на рисунке 2.2.

Такой граф, в котором вершины соединены направляющими дугами называют направленным, или ориентированным графом (сокращенно орграфом).

Дуги заходящие в какую-либо вершину и исходящие из нее, называют инцидентными этой вершине. Так, на рисунке 2.2 дуга инцидентна вершинам и . Аналогично и считаются инцидентными . Дуга, инцидентная только одной вершине (например ), называется петлей. Вершину, не инцидентную никакой дуге, называют изолированной (вершина 1 на рисунке 2.1в).

Две вершины соединенные дугой, называются смежными (например, и на рисунке 2.1). Соответственно смежными будут дуги, имеющие общую вершину ( , , и ).

Последовательность дуг , в которой конец каждой предыдущей дуги совпадает с началом последующей, называется маршрутом, или путем в графе. Принимая длину каждой дуги за единицу, длину пути можно определить по числу дуг последовательности как . Если длину каждой дуги принять равной некоторому числу , то длина пути будет определена как сумма длин дуг, входящих в путь. Рассмотренный путь может быть записан и через последовательно пройденные вершины:

.

Путь, у которого начальная вершина совпадает с конечной, называется контуром. Если все промежуточные вершины в контуре различны, а начальная и конечная совпадают, то контур считается элементарным. Очевидно, что петлю можно рассматривать как контур длиной 1.

Если отношение пары сопоставляемых вершин симметрично , то вершины соединены двумя встречно направленными дугами (рисунок 2.1б). В этом случае связь между вершинами может быть показана одной линией без стрелки. Граф, в котором отношение для любых двух вершин обладает свойством симметрии, представляет симметричное бинарное отношение и называется ненаправленным, или неориентированным графом (сокращенно неорграф). В таком графе линии между вершинами называются ребрами, а понятие пути и контура заменяются понятиями цепь и цикл.

На рисунке 2.1в изображен неорграф, представляющий отношения в примере 1.16 и аналогичный графу на рисунке 2.1б.

Если в графе отбросить часть вершин с инцидентными им дугами (ребрами), то получим подграф , имеющий множества и . На рисунке 2.2 подграф, полученный отбрасыванием вершины и дуг , и , обведен пунктиром. Если отбросить только часть дуг (ребер), оставив все вершины, то получим частичный граф , или суграф , обозначенный на рисунке 2.2 жирными дугами.

Р исунок графа зависит от расположения вершин и формы ребер (дуг). Иногда нелегко установить, одинаковы ли графы, изображенные разными рисунками, как, например, на рисунке 2.3а и б. Задача усложняется, если вершины имеют разное обозначение или нумерацию (рисунок 2.3в).

Тождественные преобразования графов путем переобозначения вершин или ребер дают изоморфные графы. Используя логический символ эквивалентности , можно записать, что графы и будут изоморфными при взаимно-однозначном соответствии и . Это означает, что если , то ребро .

Изоморфизм графов есть отношение эквивалентности на графах.