4.2.1. Характеристическое уравнение. Собственные числа и собственные векторы

Уравнение вида

,

может рассматриваться как порождение нового вектора у путем умножения матрицы А на вектор х. Если полученный таким образом вектор у совпадает в векторном пространстве по направлению с первоначальным вектором х, то составляющие вектора должны быть пропорциональны составляю­щим вектора х, т. е.

. (4.5)

Число в этом случае является коэффициентом пропорциональности.

Запишем систему (5) в развернутой форме

. (4.6)

Перейдем к однородной системе, объединяя члены, расположенные в правой и левой частях уравнения (4.6):

. (4.7)

В матричном виде

. (4.8)

Матрица отличается от А тем, что по диагонали вычитается число .

Система (4.7) имеет нетривиальное, или ненулевое, решение (т. е. такое решение, в котором хотя бы одно из чисел x_i, отличается от нуля) лишь при условии, что определитель равен нулю, а именно

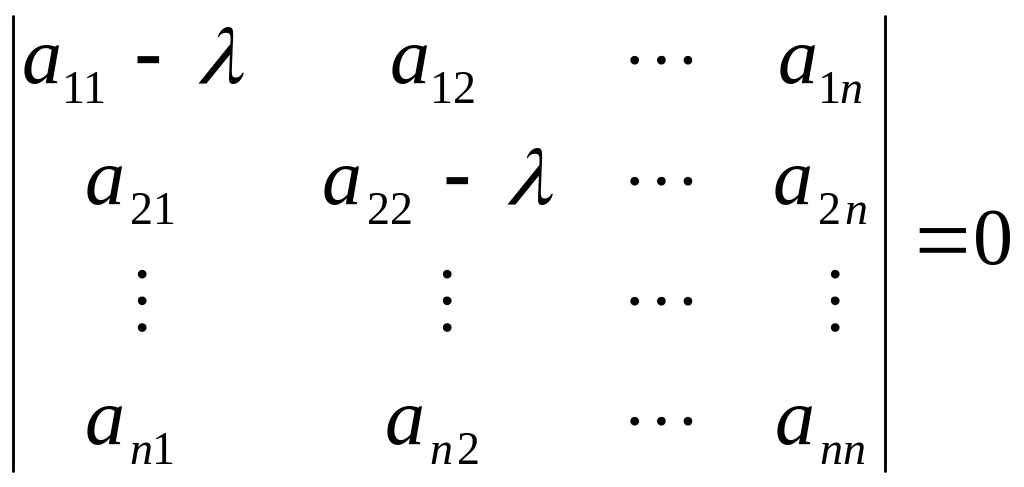. (4.9)

Перепишем уравнение (4.9) сокращенно в матричном виде

. (4.10)

Определитель называется характеристическим.

Разворачивая определитель по известным правилам, получим полином n-й степени относительно числа А. Приравнивая его к нулю, получим характеристическое уравнение

. (4.11)

Корни характеристического уравнения (4.11) называются собственными или характеристическими числами матрицы. Совокупность всех собственных чисел называется спектром матрицы А.

4.2.2. Связь между собственными числами и элементами матрицы. След матрицы

Рассмотрим две простые закономерности, связывающие собственные числа и элементы матрицы А. Они вытекают из известной теоремы Виета. Положив в уравнении (4.11) = 0, получим

. (4.12)

Следовательно, свободный член характеристического уравнения равен определителю матрицы А.

Запишем характеристический полином в виде произведения сомножителей, полагая все собственные числа _i различными:

. (4.13)

При получим

.

Следовательно, определитель матрицы А равен произведению всех собственных чисел _i. Из этого свойства следует, что если хотя бы одно из _i равно нулю, матрица А - особенная.

Уравнение в форме (4.13) дает возможность выразить коэффициенты при различных степенях л через собственные числа. Например, коэффициент при равен

. (4.14)

С другой стороны, раскрывая определитель , найдем, что коэффициент при равен сумме диагональных элементов:

. (4.15)

Таким образом, сумма диагональных, элементов матрицы равна сумме ее собственных чисел.

Ввиду важности этих свойств сумме диагональных элементов присвоено особое название - след матрицы. След матрицы А обозначается Sp А или tr А. Таким образом,

. (4.16)

Справедливы следующие соотношения:

, , , .

4.2.3. Собственные векторы

Уравнение (4.5) имеет своим решением ненулевой вектор только в том случае, если множитель пропорциональности равен хотя бы одному из собственных чисел матрицы А.

Каждая матрица размерности всегда имеет ровно n собственных чисел. Некоторые из этих собственных чисел могут быть кратными (совпадающими). Для каждого возможного значения может быть найдено решение однородной системы (4.8). Подставляя значение в уравнение (4.8), получим вектор решения

.

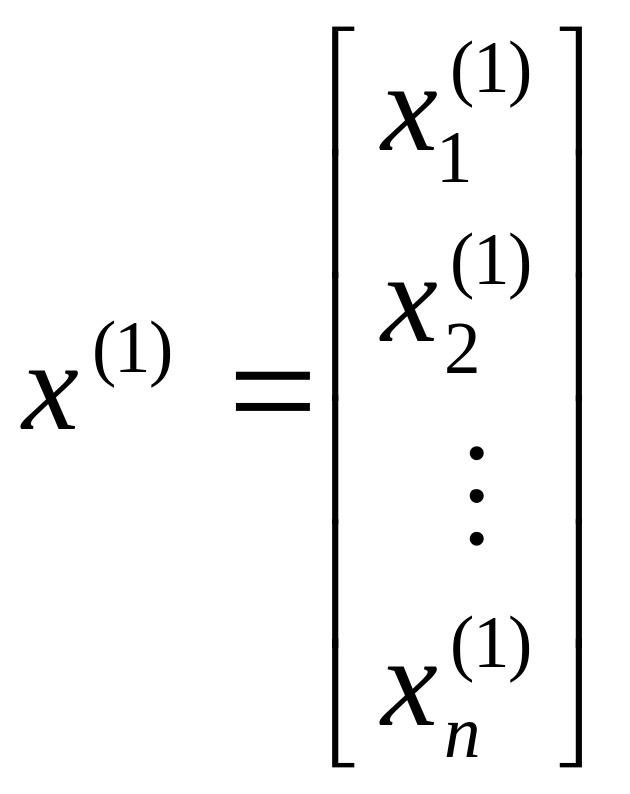Если подставить получим второй вектор решения

,

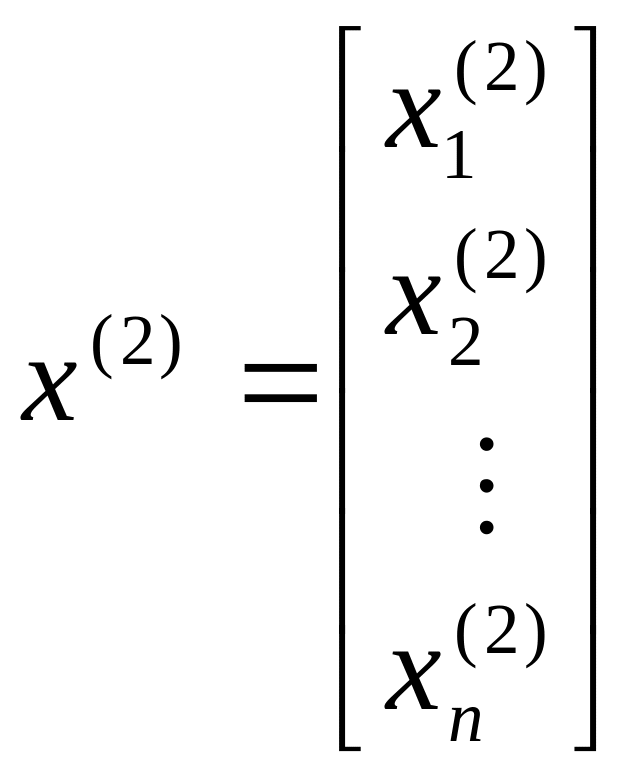и так далее, вплоть до . Последний вектор решения имеет вид

.

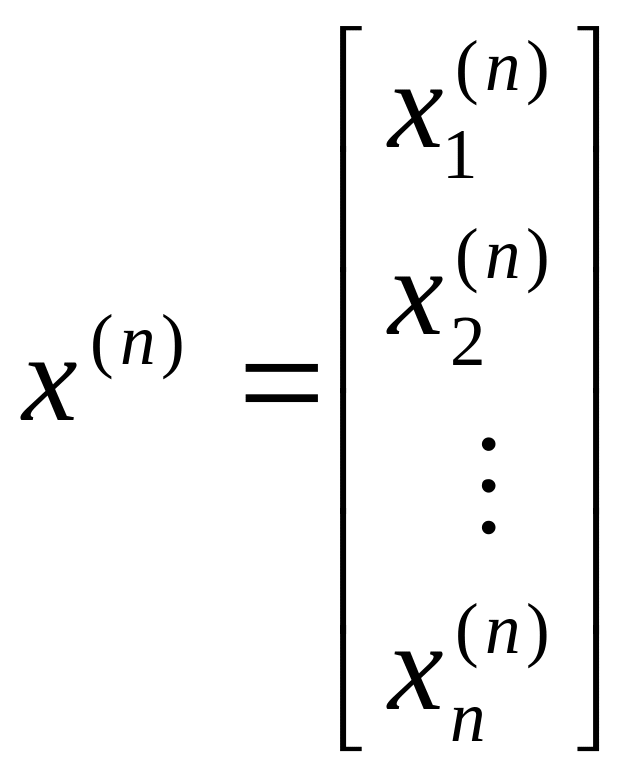Полученные векторов называются собственными векторами матрицы А. Таким образом, каждое собственное число порождает свой собственный вектор. Если собственные числа вещественной матрицы комплексны, координаты собственного вектора также будут комплексны.

Так как собственные векторы являются решениями однородной системы, то каждое решение определено лишь с точностью до произвольного ненулевого множителя, т. е. умножив решение на скалярный множитель, опять получим решение.

При умножении собственного вектора на любое произвольное, не равное нулю число изменяется лишь его длина, но направление в пространстве остается тем же. Таким образом, собственные векторы, образующие систему n решений в n мерном пространстве, однозначно определены лишь по направлению, но их длины (модули) могут быть произвольны.

Если собственные числа матрицы различны, то собственные векторы, порождаемые ими, линейно независимы. Система линейно независимых векторов образует базис пространства Rⁿ.

Примером базиса является совокупность векторов

,

,

...............................

.

Любой вектор может быть представлен в базисе из собственных векторов. В частности,

Число векторов, образующих базис, совпадает с размерностью пространства.

Если имеются кратные собственные числа, то вопрос о существовании линейно независимых векторов остается открытым. Им могут соответствовать линейно независимые собственные векторы, но могут и не соответствовать.

Отметим некоторые свойства симметрических матриц.

1) Собственные числа симметрической матрицы вещественны. Это относится также к тому случаю, когда элементы матрицы комплексно-сопряженные.

2) Собственные векторы симметрической матрицы ортогональны. Это значит, что их скалярное произведение равно нулю.

Если симметрическая матрица А имеет n различных собственных чисел то соответствующие собственные векторы образуют в n-мерном пространстве ортогональный базис.

Пример 4.4. Рассмотрим матрицу

Ее характеристическое уравнение имеет вид

Собственные числа матрицы

Найдем собственный вектор, порождаемый :

.

Одно из решений уравнения

, .

Следовательно, собственный вектор, соответствующий

.

Однако он не единственный. Решению уравнения удовлетворяет , . Поэтому собственный вектор

,

также способствует собственному числу .

Найдем собственный вектор, порождаемый

Для решения уравнения положим , . Собственный вектор, соответствующий , будет

.

Убедимся, что вектор также удовлетворяет . Эти векторы линейно независимы, следовательно, образуют базис пространства.

Пример 4.5 Рассмотрим симметрическую матрицу

, , , .

Собственные векторы

, .

При , , .

При , , .

Собственные векторы образуют ортогональный базис. Действительно, их скалярное произведение равно нулю:

Контрольные вопросы

1) Какая матрица называется треугольной?

2) Приведите примеры треугольных матриц?

3) Как определяется характеристическое уравнение матрицы?

4) Как определяются собственные вектора матрицы?