3. Обробка результатів прямих вимірювань.

Під час обробки результатів прямих вимірювань рекомендується:

1) результати кожного вимірювання внести в таблицю;

2) обчислити середнє значення з N вимірювань;

3) визначити абсолютну похибку кожного вимірювання:

∆x_i = ;

4) обчислити квадрати похибок усіх вимірювань:

(∆x₁ )², (∆x₂ )²,…, (∆x_N )²:

5) визначити середньоквадратичну похибку:

;

6) задати значення надійності Р;

7) для заданої надійності Р та кількості вимірювань N визначити

коефіцієнт Стьюдента t_P,N;

8) визначити похибку результату вимірювань: ;

9) якщо похибка вимірювань того ж порядку, що похибка приладу , то загальна похибка вимірювань

10) кінцевий результат вимірювань записати у вигляді:

11) оцінити відносну похибку результату вимірювань у відсотках

.

Приклад. За допомогою секундоміра проведено п’ять вимірювань однакових інтервалів часу. Результати вимірювань унесені в таблицю.

Таблиця

№
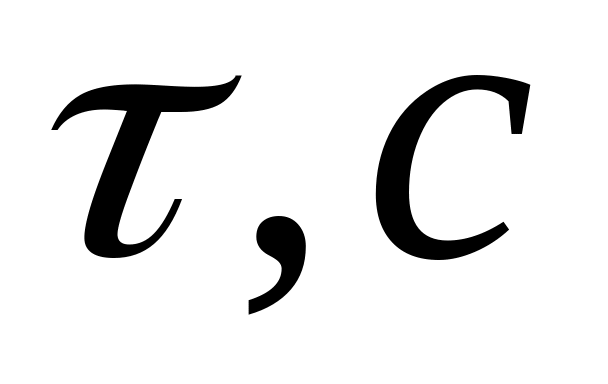
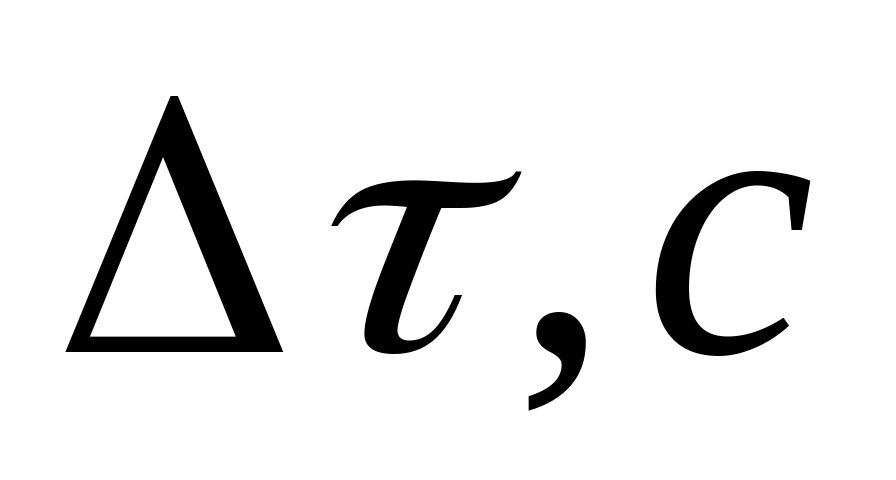
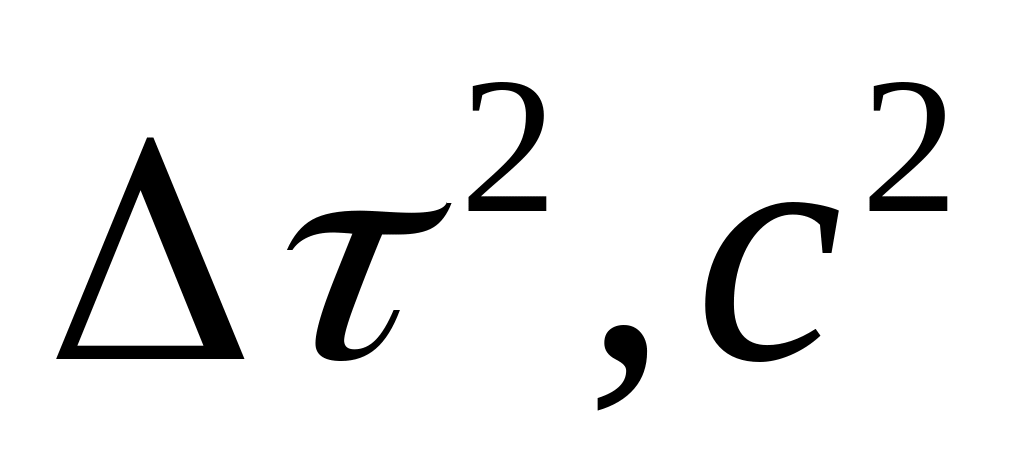
1 2 3 4 5	89,6 89,2 89,4 89,0 89,5	0,3 0,1 0,1 0,3 0,2	0,09 0,01 0,01 0,09 0.04
Сер.	89,3	0,2

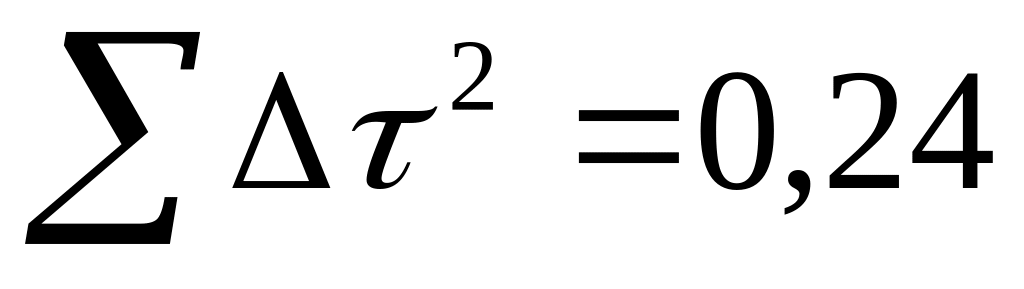
1) Розрахуємо середнє арифметичне значення інтервалу часу:

2) Розрахуємо значення похибок вимірювань: та

3) Визначимо стандартний довірчий інтервал:

4) Задаємо надійність Р = 0,95 для п`яти вимірювань і за таблицею знайдемо коефіцієнт Стьюдента:

5) Визначимо похибку вимірювань за формулою:

6) Похибка секундоміра 0,1с втричі менша, ніж похибка вимірювань, тому похибкою секундоміра можна знехтувати.

7) Результат вимірювань з надійністю Р = 95 % запишемо так:

Під час вимірювання інтервалу часу 95 вимірювань із 100 попадуть в інтервал (89,0 89,6) с.

Відносна похибка вимірювань

4. Розрахунки похибок непрямих вимірювань

Припустимо, що величину, яку вимірюють, знаходять за формулою: , де – результати прямих вимірювань фізичних величин. Похибку результатів непрямих вимірювань величини f оцінюють за формулою:

Кінцевий результат вимірювань записують у вигляді:

,

де середні значення вимірювань фізичних величин. Далі визначають відносну похибку непрямих вимірювань за формулою:

Якщо функцію можна представити у вигляді добутку , то простіше знайти відносну похибку, а потім абсолютну за такою методикою:

1) логарифмують функцію , тоді отримують:

;

2) диференціюють послідовно за a, b, c,… :

;

3) формально замінюють диференціал d на абсолютну похибку – , знаки «+» на «–» і знаходять відносну похибку непрямого вимірювання:

;

4) знаходять абсолютну похибку непрямого вимірювання:

;

Точніше абсолютну похибку непрямого вимірювання можна знайти за формулою:

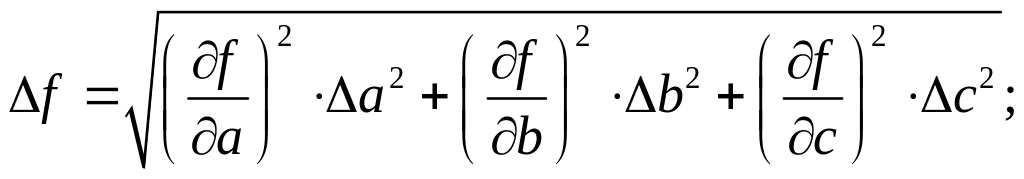
5) результат непрямих вимірювань записують у вигляді:

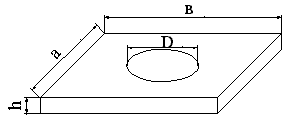
Приклад 1. Робоча формула для обчислення густини тіла, яке представлено на рисунку:

Для оцінки точності проведених вимірювань знайдемо відносну і абсолютну похибки:

;

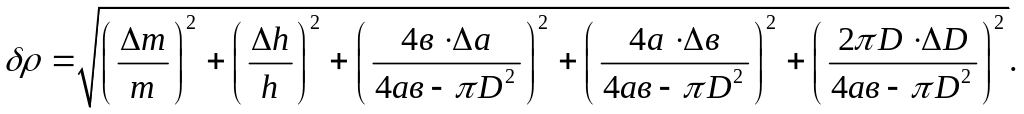
Результати вимірювань маси і розмірів тіла внесені в таблицю.

Таблиця

Пор. №			h		а	а
1 2 3 4 5	9.05 - - - -	0.05 - - - -	5.6 5.6 5.7 5.5 5.6	0.06 0.06 0.04 0.16 0.06	19.8 19.6 19.6 19.7 19.8	0.1 0 0.1 0 0.1	65.4 64.5 65.1 65.2 64.8	0.4 0.5 0.1 0.2 0.1	10 10 10 10 10	0.1 - - - -
Сер.	9.05	0.05	5.76	0.1	19.7	0.1	65.0	0.26	10	0.1

Середнє значення густини тіла:

.

Відносна і абсолютна похибки вимірювань розмірів тіла:

Густина речовини тіла:

Приклад 2. Робоча формула для обчислення моменту інерції:

де m – маса вантажу; – радіус шківа; – час; g – приско-рення вільного падіння.

Значення прямих вимірювань цих величин такі:

m = (496 1) г; R = (102,0 0,5) мм; t = (2,93 0,01) с;

h = ( 220 1) см; g = 9,81м/с².

Розрахуємо момент інерції:

I =

Знайдемо і розрахуємо похідні першого порядку:

Знайдемо абсолютну похибку результату вимірювання моменту інерції за формулою:

Відносна похибка вимірювань:

Кінцевий результат вимірювання моменту інерції: