1. Яблонский а.А. Курс теоретической механики. Ч. 2, «Высшая школа», с-Птб.: 2002 и предшествующие издания.

2. Бать м.И., Джанелидзе г.Ю., Кельзон а.С. Теоретическая механика в примерах и задачах. Ч.1 и 2. М., 1961 и последующие издания

Контрольные задания для СРС - пользуясь теоремой о движении центра масс решить самостоятельно следующую задачу: сидящий в лодке охотник стреляет вперед в горизонтальном направлении. Пренебрегая сопротивлением воды, определить скорость лодки после выстрела, если до выстрела она была неподвижна; масса охотника 70 кг, масса лодки 30 кг, масса заряда 40 г и его начальная скорость 300 м/с.

Лекция 12. Работа силы. Мощность

Цель лекции – познакомить с мерой действия силы – работой и мощностью; рассмотреть примеры вычисления работы некоторых сил

План лекции

1. Элементарная и полная работа силы. Пример. Мощность силы

2. Работа силы в различных случаях движения твердого тела

КРАТКОЕ СОДЕРЖАНИЕ ЛЕКЦИИ

Элементарная работа силы. Элементарная работа силы на элементарном перемещении определяется формулой

, (1)

где , - скорость точки приложения силы.

Величина скалярная, ее знак определяется знаком функции . Если острый угол, - тупой угол, а для , . Так как , то формулу (1) можно представить в виде:

. (2)

Таким образом, элементарная работа силы равна произведению элементарного перемещения на проекцию силы на это перемещение.

Поскольку , то, согласно (1)

, или (3)

Следовательно, элементарная работа силы равна скалярному произведению вектора силы и дифференциала радиус-вектора .

Так как , представим выражение (3) в виде:

(4)

Таким образом, элементарная работа силы равна скалярному произведению элементарного импульса силы на скорость точки ее приложения.

В аналитической форме (4) будет иметь вид:

Полная работа силы. Полную работу силы на конечном перемещении определяют как предел суммы ее элементарных работ, т.е.

, (5)

где работа силы на элементарном перемещении. Так как эта сумма является интегральной суммой определения криволинейного интеграла, то

.

Используя различные формулы для определения элементарной работы, получаем:

или .

Если же сила является функцией времени, то, согласно (4), работа силы определяется выражением:

(6)

Работа силы зависит от характера движения точки приложения силы. Например, если скорость точки приложения силы равна нулю, то .

Пример. Рассмотрим материальную точку М, на которую действует сила тяжести . Точка перемещается из положения М₀ в положение М_{1 ,} при этом координатные оси выбраны так, что ось z направлена вертикально вверх (рис.1). Проекции силы на координатные оси . Подставляя их в формулу для работы, будем иметь:

(7).

Обозначив через h=z-z₀ вертикальное перемещение, получим:

; (8)

или .

Следовательно, работа силы тяжести материальной точки равна взятому со знаком плюс или минус произведению модуля силы на вертикальное перемещение точки (при опускании точки работа положительная, при подъеме – отрицательная). Из формулы (8) следует, что работа силы тяжести не зависит от формы траектории, по которой перемещается точка ее приложения.

Единица измерения работы в системе СИ - 1 джоуль .

Мощность. Отношение приращения работы силы к элементарному промежутку времени, за которое оно произошло, называется мощностью:

.

Так как , то .

Таким образом, мощность силы равна скалярному произведению силы на скорость точки ее приложения. Единица измерения мощности в системе СИ - 1 Ватт .

Работа силы при поступательном движении твердого тела. При поступательном движении твердого тела векторы скоростей, а также элементарные перемещения всех точек тела одинаковы. Тогда элементарная работа силы

.

Полная работа силы на каком-либо перемещении будет

.

Работа силы при вращении твердого тела вокруг неподвижной оси. Разложим силу , приложенную в произвольной точке М тела, по осям естественного трехгранника (рис.2): .

Работы составляющих силы по нормали и бинормали равны нулю, ибо они направлены всегда перпендикулярно к вектору скорости точки М.

Поэтому .

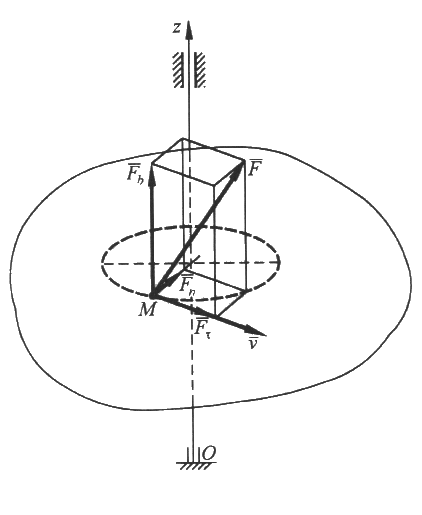Рис.2

Поскольку , то

,

где кратчайшее расстояние от точки приложения силы до оси вращения.

Учитывая, что - момент силы относительно оси , получаем:

Таким образом, элементарная работа силы, приложенной к какой-либо точке тела, вращающегося вокруг неподвижной оси, равна произведению момента этой силы относительно оси вращения на дифференциал угла поворота тела.

Полная работа

.

В случае, когда момент силы относительно оси вращения тела постоянен, полная работа .

Мощность силы в рассматриваемом случае

,

где - проекция на ось угловой скорости.

Работа силы в общем случае движения свободного тела. Скорость точки приложения силы в рассматриваемом случае равна

,

где - скорость полюса А.

Тогда .

Так как то

, или ,

где проекция на вектор ; - элементарный угол поворота тела вокруг мгновенной оси относительно вращения

Таким образом, элементарная работа силы, приложенной к какой-либо точке твердого тела, в общем случае его движения равна сумме элементарных работ силы на элементарном поступательном перемещении вместе с полюсом и элементарном вращательном перемещении вокруг мгновенной оси, проходящей через полюс.

ГЛОССАРИЙ

Күштiң элементарлық жұмысы	Элементарная работа силы	Elementary work of force
Күш жұмысы	Работа силы	Work force
Күш қуаты	Мощность силы	Power of force

Рекомендуемая литература