4 Порядок выполнения

4.1 Ознакомиться со структурой предложенных программ и команд, адресами ячеек основной памяти, кодами операций, которые предстоит выполнить.

4.2 Выполнить задание предложенное преподавателем в соответствии с приведенным ниже примером

Пример:

((11 + 24) / 5) * 7 – 3 = 46

код операции	адрес операнда		Содержание команды
01	0004		Считать 11
03	0001		Сложить 24
06	0005		Разделить 5
05	0002		Умножить 7
04	0006		Вычесть 3
02	0007		Записать в ячейку 0007
Ячейки памяти
0007		46
0008		-

5 Содержание отчёта

5.1 Название и цель занятия.

5.2 Выполненные задания.

5.3 Выводы по работе.

6 Контрольные вопросы

1. В чем заключается принцип программного управления ЭВМ?

2. Пояснить принцип однородности памяти и адресности.

3. Дать определения операнда машинной команды.

4. Какую информацию несет код операции и адресная часть команды?

5. Объяснить структуру 2-х адресной команды.

6. Объяснить структуру 4-х адресной команды.

Практическая работа № 3

Тема: Выполнение арифметических операций в ЭВМ

Цель работы: Освоить алгоритмы выполнения арифметических операций в ЭВМ

Краткие сведения из теории

Базовая операция сложения:

В основе всех арифметических операций лежит операция сложения, которая называется базовой операцией. В пределах одного разряда операция сложения может быть выполнена по следующему алгоритму:

Е

Здесь Q - основание системы счисления, awb - цифры одного разряда слагаемых.

сли S > q или S = q, то значение суммы ориентируется на значение q. А блок 7 устанавливает для следующего разряда единичное значение (появляется перенос в следующие разряды).

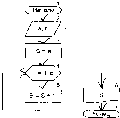
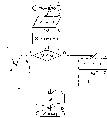
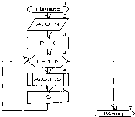
Блок 4 организует цикл из N операций, а блок 5 обращается к алгоритму 1 и сообщает ему в качестве исходных данных цифры i-того разряда А и В, а возвращает перенос P и соответствующий разряд суммы.

Считается, что результат имеет длину N, то есть перенос из N-ого разряда в N+1-ый игнорируется.

Сложение чисел с плавающей точкой:

Так как числа с разными порядками суммировать нельзя, то для сложения двух чисел в нормальной форме представления необходимо выполнить операцию выравнивания порядков.

А = m₁* q^P₁, В = m₂*q^P₂

где m₁, m2 - мантиссы, p₁ и p₂- порядки.

Необходимо предварительно привести их к общему порядку, то есть преобразовать одно из слагаемых следующим образом:

Робщ = max (pi*p₂ )

B = (m₂')*(f общ

С = А+В = m*cf = m_t*(f_общ+ т₂ '*(f₀б_щ= (т,+{т₂ '))*(f_o6„₄

Преобразованная мантисса должна быть правильной дробью, поэтому преобразованию всегда подвергается меньшее слагаемое, так как в противном случае может произойти переполнение разрядной сетки мантиссы преобразованного числа.

Мантисса может переполнить разрядную сетку, при этом использование модифицированных ко­дов позволяет не только отметить факт переполнения, но и восстановить правильный результат. Это обеспечивается сдвигом мантиссы на одну позицию в сторону младших разрядов и увеличением порядка на 1.

При сложении чисел в нормальной форме можно выделить 4 этапа:

Уравниваются порядки слагаемых. Меньший порядок увеличивается до большего, а мантисса преобразуемого числа сдвигается вправо на соответствующее число разрядов. С этой целью производится вычитание порядков чисел. Знак и модуль разности будут определять, соответственно, какое из слагаемых нужно преобразовать и на сколько нужно сдвинуть мантиссу.

Производится преобразование мантисс слагаемых в один из модифицированных кодов, дополнительный или обратный, затем производится сложение мантисс по правилу сложения чисел с плавающей точкой.

А	В	С
0	0	0
0	1	0
1	0	0
1	1	1

В случае необходимости производится нормализация результатов.

Результат переводится в прямой код, ему приписывается общий порядок и округляется.

Умножение чисел:

В двоичной системе счисления таблицы умножения описывают функцию конъюнкции. При умножении конъюнкция составляет матрицу :

				А	4	3	2	1
				В	4	3	2	1
					4х1	3х1	2х1	1х1
				4х2	3х2	2х2	1х2
			4х3	3х3	2х3	1х3
		4х4	3х4	2х4	1х4
С	27	26	25	24	23	22	21	20

Р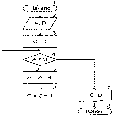 азряды сомножителей коньюкции (с 1-го по 4-ый) обозначены двузначными числами, состоящими из номеров разряда сомножителей, а для произведения С указаны веса его разрядов от 2° до 2⁷. Матрица имеет симметричный вид. Наклонные линии, содержащие коньюкции, являются произведением одного сомножителя на разряд другого. Умножение может выполняться, к примеру, по схеме:

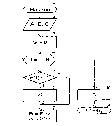Здесь А и В - множители, N - их разрядность. Начальное значение суммы S устанавливается в блоке 3. В блоке 4 организуется цикл из N итераций (повторений), выполняемых за N тактов . Блок 5 разрешает работу блока 6 лишь при значении В_t= 1 и реализует функцию коньюкторов, умножающих разряды множимого А на первый младший разряд В, множителя В. Блок 7 сдвигает на 1 позицию вправо числа В и S, при этом место младшего разряда В множителя занимает следующий по старшинству разряд. По окончанию всех итераций блок 8 выводит S - результат умножения.

В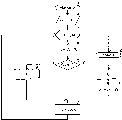 данном способе вычисления выполняются начиная с младшего разряда множителя В с изменением взаимного положения чисел S и А путём сдвига суммы S.

Деление чисел:

Операция деления выполняется над числами А - делимым и В - делителем. Её результатом является частное С и остаток D.

A = BC + D,\D\<B

Операция деления реализуется через многократное вычитание делителя В из делимого А. Это достигается сложением чисел в обратном и дополнительном кодах. Наиболее простой способ деления описывает алгоритм последовательного вычитания рис.5:

Если условие А < В не выполняется, то число А уменьшается на величину В, при этом значение частного увеличивается на 1 и происходит возврат к блоку 4. Если выполняется условие А < В, мы выводим частное С и остаток D.

Описанный алгоритм относится к целочисленному делению и применяется для выполнения операций над числами в естественной форме представления (то есть с фиксированной точкой). Числа с плавающей точкой обрабатываются с использованием точностного деления, которое выполняется над нормализованными мантиссами чисел.

Точностное деление определяет частное с заданным количеством разрядов, а остаток игнорируется. Такое деление характеризуется алгоритмом с восстановлением остатка.

Порядок выполнения:

• Изучить и законспектировать краткие сведения из теории;

• Провести вычисления: Умножить свой день рождения на месяц рождения. Результат сложить с годом рождения и разделить на 365₁₀.

• Оформить отчёт.

Содержание отчёта:

Цель работы

Конспект теоретического материала

Вычисления в соответствии с заданием

Выводы по результатам работы.