Характеристики списков. Длина списка. Количество элементов в списке

Списки могут быть типизированными или нетипизированными. Если список типизирован, то тип его элементов задан, и все его элементы должны иметь типы, совместимые с заданным типом элементов списка. Обычно списки, реализованные при помощи массивов, являются типизированными.

Список может быть сортированным или несортированным

В зависимости от реализации может быть возможен произвольный доступ к элементам списка.

Массив — упорядоченный набор данных, для хранения данных одного типа, идентифицируемых с помощью одного или нескольких индексов. В простейшем случае массив имеет постоянную длину и хранит единицы данных одного и того же типа.

Количество используемых индексов массива может быть различным. Массивы с одним индексом называют одномерными, с двумя — двумерными и т. д. Одномерный массив нестрого соответствует вектору в математике, двумерный — матрице. Чаще всего применяются массивы с одним или двумя индексами, реже — с тремя, ещё большее количество индексов встречается крайне редко.

Динамическим называется массив, размер которого может меняться во время исполнения программы. Для изменения размера динамического массива язык программирования, поддерживающий такие массивы, должен предоставлять встроенную функцию или оператор. Динамические массивы дают возможность более гибкой работы с данными, так как позволяют не прогнозировать хранимые объёмы данных, а регулировать размер массива в соответствии с реально необходимыми объёмами. Обычные, не динамические массивы называют ещё статическими.

Алгоритмы обработки одномерных числовых массивов

Под структурой данных типа массив понимают однородную структуру однотипных данных, одновременно хранящихся в последовательных ячейках оперативной памяти. Эта структура должна иметь имя и определять заданное количество данных (элементов). Однотипность данных определяет возможность использования циклических алгоритмов для обработки всех элементов массива. Количество итераций цикла определяется количеством элементов массива. Одновременное хранение в памяти всех элементов массива позволяет решать большой набор задач, таких как, поиск элементов, упорядочение и изменение порядка следования элементов.

Доступ к любому элементу массива осуществляется по его номеру (индексу). Поэтому для обращения к элементу массива используют имя массива (номер элемента), например: А(5).

Рассмотрим несколько более сложных алгоритмов, в которых осуществляется изменение порядка следования элементов в одномерном массиве. К таким алгоритмам относят алгоритмы с перестановкой элементов местами, алгоритмы удаления некоторых элементов или циклического переноса некоторых элементов в начало или конец массива. Основным требованием при составлении алгоритмов обработки массивов является использование минимально необходимых переменных. Чтобы точнее уяснить постановку задачи следует сначала рассмотреть частные решения для некоторых значений входных данных (провести анализ), затем обобщить полученное решение и определить набор решаемых задач. Составив визуальный алгоритм, его следует проверить на различных наборах исходных данных. Эти наборы исходных данных требуется подбирать таким образом, чтобы при заполнении таблиц трассировок проверить все пути вычислений данного алгоритма от начальной вершины до конечной.

Пример. Составить алгоритм определения в одномерном числовом массиве А из N элементов суммы положительных элементов.

Решение. Алгоритм представлен на рисунке 4.1. В этом алгоритме переменная К - является счетчиком элементов массива, S - сумма элементов массива, она вычисляется по формуле S=S+A(K). Ввод количества и значений элементов массива осуществляется вначале в отдельном блоке ввода.

нет

да

да

нет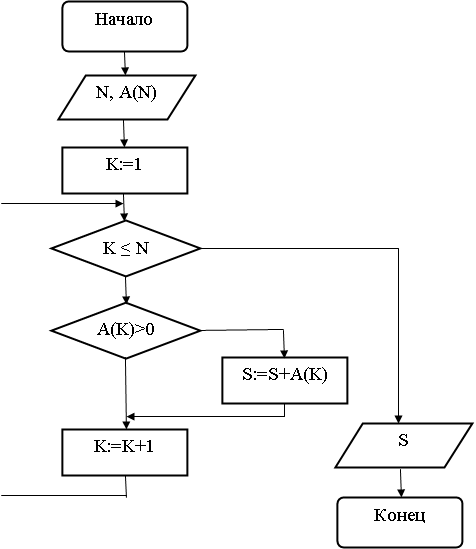

Рисунок 1- Алгоритм вычисления суммы положительных элементов

Стек (англ. stack — стопка) — структура данных с методом доступа к элементам LIFO (англ. Last In — First Out, «последним пришёл — первым вышел»). Чаще всего принцип работы стека сравнивают со стопкой тарелок: чтобы взять вторую сверху, нужно снять верхнюю.

Добавление элемента, называемое также проталкиванием (push), возможно только в вершину стека (добавленный элемент становится первым сверху). Удаление элемента, называемое также выталкивание (pop), возможно также только из вершины стека, при этом, второй сверху элемент становится верхним.

Стеки широко применяются в вычислительной технике — в частности, для отслеживания точек возврата из подпрограмм используется стек вызовов, который является неотъемлемой частью архитектуры большинства современных процессоров. Языки программирования высокого уровня также используют стек вызовов для передачи параметров при вызове процедур

О́чередь — структура данных с дисциплиной доступа к элементам «первый пришёл — первый вышел» (FIFO, First In — First Out). Добавление элемента (принято обозначать словом enqueue — поставить в очередь) возможно лишь в конец очереди, выборка — только из начала очереди (что принято называть словом dequeue — убрать из очереди), при этом выбранный элемент из очереди удаляется.