1.4. Ограниченное множество. Существование граней у ограниченного множества
Определение.
Множество действительных чисел
называется ограниченным снизу, если
существует действительное число
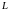такое, что для любого числа
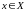справедливо неравенство
.
Это число
будем называть нижней границей множества
.
Определение.
Множество действительных чисел
называется ограниченным сверху, если
существует действительное число
такое, что для любого числа
справедливо неравенство
.
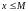Это число
будем называть верхней границей множества
.
Определение.
Множество действительных чисел
называется ограниченным, если существует
действительное число
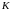такое, что для любого числа
справедливо неравенство
.
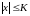Определение.
Множество действительных чисел
называется неограниченным, если для
любого действительного числа
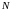существует число
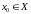для которого справедливо неравенство
.
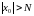Определение. Число называется верхней гранью числового множества , если
1)
для любого числа
справедливо неравенство
;
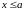2)
для любого положительного числа
существует число
такое, что
.
Верхняя
грань числового множества
обозначается
символом
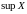(от
латинского supremum – наибольший).
Из определения следует, что верхняя грань числового множества – это наименьшая из верхних границ этого множества.
Определение. Число называется нижней гранью числового множества , если
1)
для любого числа
справедливо неравенство
;
2)
для любого положительного числа
существует число
такое, что
.
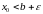Нижняя
грань числового множества
обозначается
символом
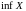(от латинского infimum – наименьший).
Из определения следует, что нижняя грань числового множества – это наибольшая из нижних границ этого множества.
Теорема 1.4.1. Всякое ограниченное сверху непустое множество имеет верхнюю грань и притом только одну.
Доказательство.
Пусть
–
ограниченное сверху множество. Тогда
существует действительное число
такое, что для любого числа
справедливо неравенство
.
Рассмотрим два возможных случая.
1
случай. Пусть какая-то из верхних границ
множества
принадлежит этому множеству. Назовем
эту границу
.
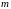Тогда для любого числа
справедливо неравенство
и для любого положительного числа
справедливо неравенство
.
То есть для этой границы выполняются
условия определения верхней грани, а,
значит, число
является верхней гранью множества
.
И утверждение теоремы справедливо.
2 случай. Пусть все верхние границы множества не принадлежат этому множеству.
В
этом случае разобьем множество всех
действительных чисел
на классы. Один класс пусть состоит из
чисел
,
которые являются верхними границами
множества
.
Этот класс назовем вторым. Остальные
числа пусть составляют первый класс.
То есть, первый класс состоит из чисел
,
для которых существует число
такое, что
.
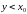(Это отрицание того, что число
не
является верхней границей множества
.)
Покажем теперь, что для этих классов выполняется условие аксиомы Дедекинда.
1)
Множество
– непустое. Значит, существует число
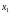из этого множества. Поэтому, число
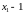меньшее
,
не будет верхней гранью множества
,
а, значит, принадлежит первому классу.
Поэтому первый класс – непустое множество
чисел.
2) Число принадлежит второму классу. Поэтому второй класс – непустое множество чисел.
3) Первый класс чисел – это дополнение второго класса до множества всех действительных чисел. Поэтому классы разбивают все множество действительных чисел.
4)
Пусть
–
произвольное число из первого класса,
а
– из второго.
Тогда существует число
такое, что
и справедливо неравенство
.
Отсюда следует, что
.
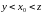Значит
.
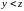Поэтому все числа первого класса меньше
каждого из чисел второго класса.
Таким
образом, условие аксиомы VI1 множества
выполнено. Тогда существует число
,
которое или принадлежит первому классу
и оно больше всех чисел этого класса
или принадлежит второму классу и оно
меньше всех чисел этого класса. Тогда
для произвольных чисел
из первого класса и
из второго
класса справедливы неравенства
.
То
есть для любого числа
справедливы неравенства
и
.
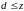Значит,
–
наименьшая из верхних границ множества
.
Поэтому число
является верхней гранью множества
.
Единственность
верхней грани доказывается методом “от
противного”. Пусть числа
и
различные верхние грани множества
.
Тогда, из минимальности верхней грани
среди верхних границ следует, что
и
.
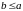Тогда
.
Утверждение теоремы справедливо.
Замечание. Покажем (другим способом) по определению, что верхняя грань множества .
Неравенства
справедливы для произвольного числа
из множества
.
То есть для любого числа
справедливо неравенство
.
Кроме того, для любого положительного
числа
число
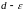меньше
(которое наименьшее во втором классе).
Значит,
принадлежит первому классу. А первый
класс состоит из чисел
,
для которых существует число
такое, что
.
Поэтому существует число
такое, что
.
То есть для
выполняются условия определения
верхней грани, а, значит, число
является верхней гранью множества
.
Аналогично доказывается симметричная теорема.
Теорема 1.4.1.а. Всякое ограниченное снизу непустое множество имеет нижнюю грань и притом только одну.