Комбинаторика

1. У одного студента 3 книги, а у другого - 4. Сколькими способами студенты могут произвести обмен а) одной книги на одну? 2) двух книг на две? 3) трех книг на три?

2. На окружности выбрано 7 точек. Сколько хорд с концами в этих точках можно провести? Сколько треугольников с концами в этих точках можно построить ?

3. Сколько различных цветных полосатых флагов можно сшить из полосок трех различных цветов?

4. Сколькими способами из 10 спортсменов можно отобрать 5 человек в команду?

5. Сколько нужно словарей, чтобы осуществлять переводы с любого из языков: английского, французского, немецкого, русского, украинского и обратно?

6. Сколькими способами можно расположить на книжной полке 10 различных книг?

7. Сколькими способами можно расположить на книжной полке 3 одинаковых учебника по математике, 2 одинаковых учебника по английскоми языку, 4 одинаковых учебника по экономике и один учебник по истории?

8. Сколькими способами можно расставить на стоянке 7 различных автомобилей с учетом пожелания чтобы два определенных автомобиля стояли рядом?

9. Сколькими способами можно расставить на стоянке 7 различных автомобилей с учетом пожелания чтобы два определенных автомобиля не стояли рядом?

10. Сколько существует различных идентификационных кодов, состоящих из 6 цифр, если код не должен начинаться с цифры 0 ?

11. Сколькими способами можно расставить в экспозиции музея 10 экспонатов при условии, чтобы а) два определенных экспоната оказались рядом; б) три определенных экспоната оказались рядом; в) четыре определенных экспоната оказались рядом.

12. Группа учащихся изучает семь предметов. Сколькими способами можно составить расписание занятий на понедельник, если в этот день недели может быть четыре различных урока?

13. Сколько матчей будет сыграно в футбольном чемпионате с участием 16 команд, если каждые две комнды встречаются между собой один раз?

14. В соревнованиях на первенство по футболу принимают участие 12 команд. Сколькими способами могут быть распределены между командами золотая, серебряная и бронзовая медали?

15. Сколько букв русского алфавита может быть передано азбукой Морзе, состоящей из точек и тире, если для передачи одной буквы отводить а) ровно 4 позиции, 5) ровно 5 позиций?

16. Номер автомобиля состоит из 2 букв латинского алфавита и четырех значного числа. Сколько существует автомобильных номеров?

17. Сколько различных шестизначных шифров можно получить из цифр 1, 2, 3 ,4, 5, 6 ,7 8, 9, если каждый шифр должен состоять из 3 четных и 3 нечетных цифр, и каждая из цифр должна входить только один раз?

18. В метро продают розы четырех различных оттенков. Сколько существует вариантов составить букет из 3 роз?

19. В магазине продаются 10 различных видов ручек. Сколько существует вариантов купить а) две различные ручки? б) две одинаковые ручки? в) любые две ручки?

ПРОСТРАНСТВО СОБЫТИЙ

1. Бросаются две игральные кости. Пусть А и В – следующие события:

А = ,

В = .

Описать события а) , б) , в) А , г) А .

2. Из колоды карт вытаскивают 3 карты. Пусть Пусть А , В, С – следующие события:

А= ,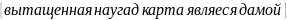

В = ,

С = .

Описать события а) , б) , в) А , г) А , д) А , е) .

3. Пусть A= ;

B= .

Изобразить на рисунках A, B, А , , A/B, B/A.

4. Пусть A= ;

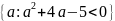B= .

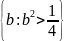Изобразить на рисунках A, B, А , , A/B, B/A.

КЛАССИЧЕСКАЯ ВЕРОЯТНОСТЬ

1. В коробке находится 20 кнопок, из них 5 бракованных. Наугад взяли 10 кнопок. Найти вероятность того, что среди них а) нет бракованных; б) ровно 1 бракованная; в) ровно 2 бракованые.

2. Из колоды 36 карт вынуты 3 карты. Какова вероятность того, что а) две из них бубновой масти; б) две из них одной масти; в) хотя бы одна из них бубновой масти; г) хотя бы одна из них – туз?

3. Колода карт делится случайным образом на две половины. Какова вероятность, что в каждой части оказалось ровно по два туза?

4. Какова вероятность того, что в четырехзначном номере случайно выбранного в большом городе автомобиля

а) все цифры одинаковые;

б) ровно три одинаковые цифры;

в) ровно две одинаковые цифры;

г) все цифры разные.

5. На полке в случайном порядке раставлены 20 книг, среди которых находится двухтомник Д. Лондона. Предполагая, что различные расположения книг равновероятны, найти вероятность того, что эти два тома расположены рядом.

6. В картотеке 20 пронумерованных карточек. Наугад вынимают одну за другой и номера записывают. Какова вероятность того, что номера будут идти а) в порядке возрастания : 1, 2 , 3…20 ; б) в порядке убывания : 20, 19 … 1 в) цифра 1 будет стоять на первом месте, а цифра 5 – на последнем?

7. Задано множество целых чисел: 1, 2 ,3 … 30. Наугад из этого множества выбирают одно число. Какова вероятность, что это число окажется кратным 5 или кратным 7?