Иррациональные уравнения

В уравнениях , неизвестное находится под знаком корня. Такие уравнения называют иррациональными. Приведём ещё примеры иррациональных уравнений: , .

Иррациональные уравнения часто получаются при решении различных задач. Решение иррациональных уравнений основано на следующем принципе:

возведение обеих частей уравнения в натуральную степень.

При возведении в натуральную степень могут появиться посторонние корни, поэтому необходима проверка.

Примеры решения задач:

Задача 1: Решить уравнение .

Решение: Возводя обе части уравнения в квадрат, получаем

, откуда

Возведём последнее уравнение в квадрат: , или .

Корни этого уравнения . Проверка показывает, что - посторонний корень.

Ответ: .

Задача 2: Решить уравнение .

Решение: Возведём уравнение в четвёртую степень: , откуда . Решим это биквадратное уравнение: , т.е. или . Уравнение имеет два корня , а уравнение

корней не имеет. Проверка показывает, что - посторонний корень

Ответ: .

Задача 3: Решить уравнение

Решение: Возведя обе части уравнения в куб, получаем , откуда

; . Корни этого уравнения . Проверка показывает, что оба значения неизвестного являются корнями исходного уравнения.

Ответ:

Упражнения для самостоятельного решения

1. Решить уравнение:

1) ; 2) ; 3) ; 4) ; 5) ; 6) 7) ; 8) ; 9) ; 10) ; 11) ; 12) ; 13) ; 14)

Показательная функция

Показательная функция, ее свойства и график

Определение: Показательной функцией называется функция , где - заданное число, .

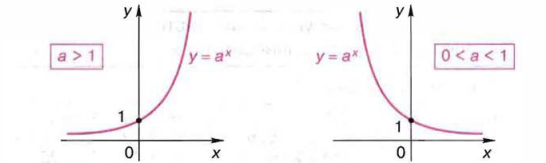
Свойства показательной функции

1. Область определения функции – множество всех действительных чисел.

2. Область значений функции - множество всех положительных чисел.

3. Монотонность функции –

Если функция является возрастающей на множестве всех действительных чисел;

Если функция является убывающей.

4. Графики всех показательных функций проходят через точку и расположены выше оси Ох, т.к. .

Решение показательных уравнений и неравенств

Решение показательных уравнений часто сводится к решению уравнения , что равносильно .

Примеры: Решить уравнения

Решение показательных неравенств зависит от монотонности показательной функции, входящей в данное неравенство.

Примеры:

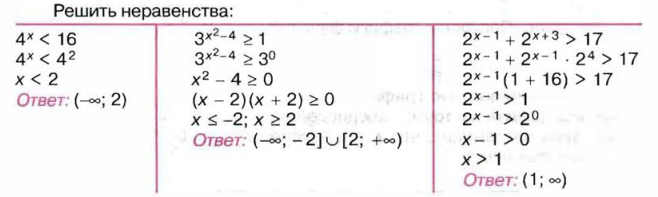
Системы показательных уравнений и неравенств

Известные способы решения систем алгебраических уравнений и неравенств применяют и к решению систем, содержащих показательные уравнения и неравенства.

Задача 1. Решить систему уравнений:

Решим эту систему способом подстановки: выразим из первого уравнения и подставим во второе уравнение .

Откуда .

Найдём значения : .

Ответ: .

Задача 2. Решить систему уравнений:

Обозначим . Тогда система запишется так:

Решим эту систему способом подстановки: ,

.

Найдём значения : . Возвратимся к принятым обозначениям:

1) . Так как первое из этих уравнений корней не имеет, то решений системы в этом случае нет.

2) , откуда .

Ответ: .