Арифметический корень натуральной степени
Уравнение
имеет два решения:
и
.
Это числа, квадрат которых равен 4.
Рассмотрим
уравнение
.
Нарисуем график функции
и увидим, что и у этого уравнения два
решения, одно положительное, другое
отрицательное.
Но в данном случае решения не являются целыми числами. Более того, они не являются рациональными. Для того чтобы записать эти иррациональные решения, мы вводим специальный символ квадратного корня.
Арифметический
квадратный корень
— это неотрицательное число, квадрат
которого равен
,
a
≥ 0. При a
< 0 — выражение
не определено, т.к. нет такого
действительного числа, квадрат которого
равен отрицательному числу
.
Корень из квадрата
Например,
.
А решения уравнения
соответственно
и
.
Кубический
корень из числа
— это число, куб которого равен
.
Кубический корень определен для всех
.
Его можно извлечь из любого числа:
.
Корень -й степени из числа — это число, -я степень которого равна .
Пример:
Степень с рациональным показателем
Рассмотрим степень
,
где
.
.
Если
,
то по определению
(при
).
Например,
.
.
Если
,
то по определению
(при
).
Например,
;
;
;
.
.
Рассмотрим степень
,
где
-
рациональное число. Выражение
имеет в общем виде смысл только при
.
Если
,
то по определению
.
Например,
.
Выражение
или
смысла не имеет.
.
Степень с рациональным показателем
обладает теми же свойствами, что и
степень с натуральным показателем, а
именно, если
и
,
то:
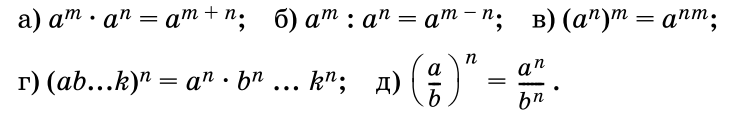
Упражнения для самостоятельного решения
1. Представить в виде степени с рациональным показателем:
2. Представить в виде корня из степени с целым показателем:
3. Вычислите:
1)
2)
;
;
;
;
.
3)
;
.
4. Найдите значение выражения:
1)
при
;
2)
при
;
3)
при
.
5. Представить в виде степени с рациональным показателем:
1)
;
2)
Решение линейных, квадратных уравнений, неравенств
Равенство, содержащее неизвестное число, обозначенное буквой, называется уравнением.
Выражение, стоящее слева от знака равенства, называется левой частью уравнения, а выражение, стоящее справа от знака равенства, - правой частью уравнения. Каждое слагаемое левой или правой части уравнения называется членом уравнения.
Корнем уравнения называется то значение неизвестного, при котором это уравнение обращается в верное равенство.
Например,
число 1 является корнем уравнения
,
так как
- верное равенство.
Уравнение
может иметь два корня, три корня и т.д.
Например, уравнение
имеет два корня: 1 и 2, так как при
и при
это уравнение обращается в верное
равенство, а при других значениях
левая часть уравнения не равна нулю.
Упражнения для самостоятельного решения
Решить уравнения:
1.
2.
3.
4.
5.
6.
7.
8.
9.
(9х
– 7)(4 + х)(3
– 2х)=0
10.
Решить неравенства:
1. 2х – 7 < 0 2. 5 - 3х > 7 - 5х
3.
4. 11х
-15 < 7 + 4х
5.
6.
7.
8.
0