6. Моделирование

Итак, мы определили, что исходный процесс лучше всех остальных моделей приближают модели АР(3), СС(0), АРСС(3,3). Смоделируем случайную последовательность. При этом нужно учесть, что при нулевых начальных условиях сгенерированная случайная последовательность приобретает свойство стационарности по истечении интервала времени, много большего, чем радиус корреляции. Поэтому нужно было сгенерировать 6000 отсчётов последовательности и отбросить первые 1000 отсчётов, считая их «браком».

Используем формулу:

1. В среде Scilab создадим вектор (с помощью функции grand) с координатами, распределенными по нормальному закону с нулевым математическим ожиданием и единичной дисперсией (так называемый «белый шум»).

2. В результирующий вектор будем записывать значения моделируемого процесса по формуле:

Для АР(3):

Для СС(0):

Для АРСС(3,3): где - -ая координата результирующего вектора выходного процесса

– -ая координата нормального вектора выходного процесса

3. Так как в полученном векторе находится случайная последовательность с математическим ожиданием, близким к нулю, прибавим к нему значение выборочного среднего, найденного в пункте 1.

Результаты моделирования каждой модели представлены на рисунках 3, 4, 5. Чёрным цветом на рисунке обозначен исходный процесс, зеленым – смоделированный, синим – математическое ожидание, красным – границы средне квадратичного отклонения.

Рисунок 3 – Фрагмент реализации модели АР(3)

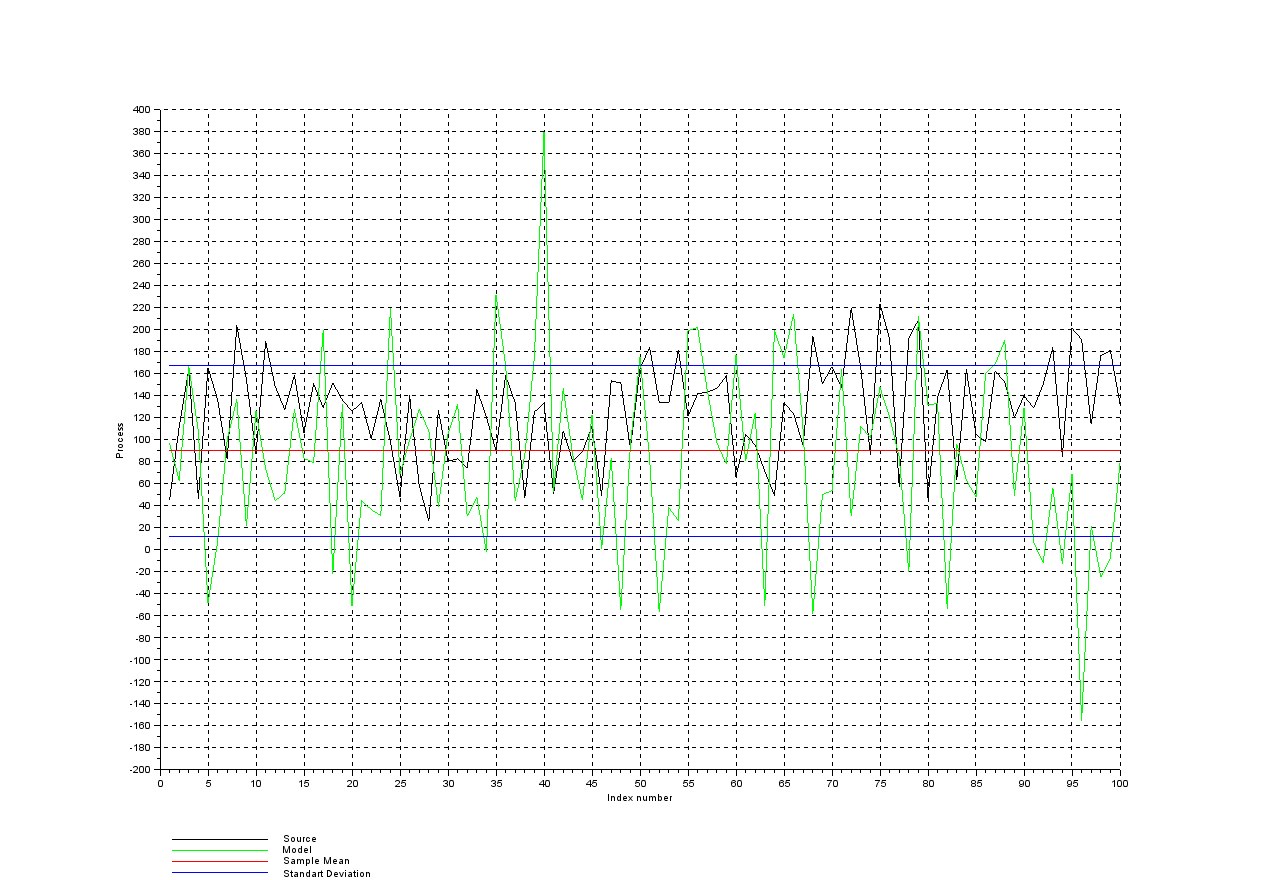
Рисунок 4 – Фрагмент реализации модели СС(0)

Рисунок 5 – Фрагмент реализации модели АРСС(3,3)

7. Оценка моментных функций смоделированного процесса

Найдем оценки моментных функций случайных последовательностей, полученных в п. 6, используя те же формулы, что и в пункте 1.

Таблица 6 – Сравнение моментных функций

Параметры процесса	Исходный процесс		АР(3)					СС(0)					АРСС(3,3)
			Теория		Выборка		Теория			Выборка		Теория			Выборка
Минимум	-185.1580				-134.0462					-158.3429					-197.9851
Максимум	343.7910				315.1875					380.4468					353.0161
Среднее	90.1462				82.4516					90.8202					84.2323
Дисперсия	6052.3322				4996.8378					6133.9469					5509.2607
СКО	77.7967		77.7967		70.6883		77.7967			78.3195		77.7967			74.2244
Нормированная корреляционная функция
r(0)	1.0000		1.0000		1.0000		1.0000			1.0000		1.0000			1.0000
r(1)	0.7484		0.7484		0.7027		0			-0.0230		0.7484			0.7235
r(2)	0.7485		0.7485		0.7021		0			-0.0278		0.7485			0.7242
r(3)	0.8832		0.8832		0.8563		0			0.0100		0.8832			0.8674
r(4)	0.7048		0.7321		0.6804		0			-0.0035		0.7048			0.6712
r(5)	0.7007		0.7300		0.6787		0			-0.0263		0.7007			0.6678
r(6)	0.7263		0.7995		0.7573		0			0.0149		0.7263			0.6864
r(7)	0.6445		0.7069		0.6486		0			-0.0216		0.6426			0.5972
r(8)	0.6320		0.7024		0.6445		0			-0.0069		0.6302			0.5856
r(9)	0.6297		0.7357		0.6825		0			-0.0273		0.6217			0.5611
r(10)	0.5810		0.6772		0.6169		0			-0.0126		0.5762			0.5209
СКО		0.0363		0.0363		4.9644			4.9644		0.0001			0.0001

Где СКО – средне квадратичное отклонение.

Графически сравним выборочную нормированную корреляционную функцию исходного процесса, выборочную и теоретическую.

Рисунок 6 – Нормированные корреляционные функции

На рис.6 красным цветом обозначена нормированная корреляционная функция исходного процесса, черным – выборочная , а зеленым – теоритическая нормированная корреляционная функция модели АР(3) .

Рисунок 7 – Нормированные корреляционные функции

На рис.7 красным цветом обозначена нормированная корреляционная функция исходного процесса, черным – выборочная, а малиновым – теоритическая нормированная корреляционная функция модели СС(0) .

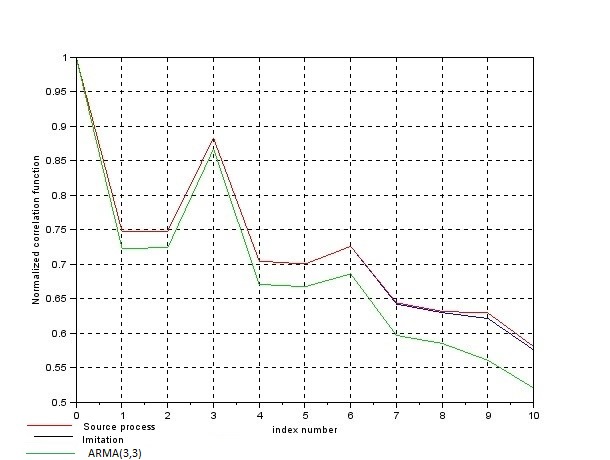
Рисунок 8 – Нормированные корреляционные функции

На рис.8 красным цветом обозначена нормированная корреляционная функция исходного процесса, зеленым – выборочная, а черным – теоритическая нормированная корреляционная функция модели АРСС(3,3) .

Вывод

В ходе работы было выполнено моделирование неизвестного эргодического процесса. Была проанализирована выборка из отсчётов исходного процесса, построены модели АР порядков М = 1, 2, 3 и все модели СС порядков N = 0, 1, 2, 3. Лучшими моделями в каждом классе оказались АР(3), СС(0). Также построены двумя способами все смешанные модели АРСС до третьего порядка включительно, лучшая модель - АРСС(3,3).

Из таблицы коэффициентов и погрешностей смешанных моделей АРСС видно, что первый и второй методы почти не отличаются в точности, но первый метод приоритетней, так как работает быстрее, но также сложен в реализации.

По лучшим моделям были смоделированы последовательности и сравнены их числовые характеристики, наиболее точно имитирует исходный процесс модель АРСС(3,3).