МИНИСТЕРСТВО ОБРАЗОВАНИЯ И НАУКИ РОССИЙСКОЙ ФЕДЕРАЦИИ

Федеральное государственное бюджетное образовательное учреждение

высшего профессионального образования

«САМАРСКИЙ ГОСУДАРСТВЕННЫЙ АЭРОКОСМИЧЕСКИЙ УНИВЕРСИТЕТ

имени академика С.П.КОРОЛЕВА (национальный исследовательский университет)»

ФАКУЛЬТЕТ ИНФОРМАТИКИ

КАФЕДРА ТЕХНИЧЕСКОЙ КИБЕРНЕТИКИ СТАТИСТИЧЕСКИЙ АНАЛИЗ И МОДЕЛИРОВАНИЕ

ПРОЦЕССОВ АВТОРЕГРЕССИИ И СКОЛЬЗЯЩЕГО СРЕДНЕГО

курсовая работа по дисциплине «Теория случайных процессов»

Вариант № 8

Выполнил: Маркеев А.А. гр.6307

Проверил: Храмов А.Г.

Оценка: _____________________

Самара 2013

Оглавление

Задание 3

1. Моментные функции исходного процесса 4

2. Модель АР(M) порядков M=1,2,3 6

3. Модель CC(N) порядков N=0,1,2,3 8

4. Модель АРСС(M,N) порядков M=1,2,3 N=1,2,3 10

5. Теоретические нормированные корреляционные функции моделей 14

6. Моделирование 17

7. Оценка моментных функций смоделированного процесса 20

Вывод 23

Приложение 24

Задание

Дана реализация стационарного в широком смысле эргодического случайного процесса с дискретным временем (стационарная случайная последовательность, временной ряд) – выборка из 5000 последовательных значений (отсчётов) процесса:

45.459 112.442 164.058 46.674 165.888 136.509 82.633 204.172 155.357 87.286 189.461 148.624 127.564 158.749 106.802 151.107 129.533 151.835 136.258 126.173 134.116 101.535 137.048 98.562 48.028 140.308 58.615 26.347 126.789 80.704

...

183.962 150.137 174.343 153.891 152.768 126.430 143.008 118.582 159.335 132.302

1. Оценить моментные функции случайного процесса, рассчитав выборочное среднее, выборочную дисперсию и выборочную нормированную корреляционную функцию. Оценить радиус корреляции случайного процесса. Изобразить графически оценку нормированной корреляционной функции.

2. Построить модели авторегрессии порядков на основе решения системы уравнений Юла-Уокера. Для каждой модели рассчитать теоретические нормированные корреляционные функции выходной последовательности. На основе сравнения выборочной и теоретической нормированных корреляционных функций выбрать наилучшую (наиболее адекватную) модель случайного процесса.

3. Построить модели скользящего среднего порядков на основе решения системы нелинейных уравнений. Для каждой модели рассчитать теоретические нормированные корреляционные функции выходной последовательности. На основе сравнения выборочной и теоретических нормированных корреляционных функций выбрать наилучшую модель случайного процесса.

4. Построить смешанные модели авторегрессии – скользящего среднего до третьего порядка включительно ( ). Рассчитать теоретические нормированные корреляционные функции выходной последовательности. На основе сравнения выборочной и теоретических нормированных корреляционных функций выбрать наилучшую модель случайного процесса. Сравнить параметры смешанных моделей АРСС, рассчитанные по двум методам. Для второго метода рассчитать и изобразить графически нормированную корреляционную функцию промежуточной случайной последовательности.

5. Для наилучшей модели:

   1. записать системы уравнений для расчёта параметров,

   2. записать системы уравнений для расчёта теоретической корреляционной функции,

   3. смоделировать случайный процесс,

   4. сравнить графически фрагменты реализаций исходного и смоделированного процессов,

   5. сравнить графически выборочную нормированную корреляционную функцию смоделированного процесса с выборочной нормированной корреляционной функцией исходного процесса и с теоретической нормированной корреляционной функцией.

6. Построить оценки моментных функций смоделированного процесса, сравнить их с оценками моментных функций исходного процесса и с теоретическими моментными функциями, соответствующими выбранным моделям.

1. Моментные функции исходного процесса

Дан стационарный в широком смысле эргодический дискретный случайный процесс η, представленный в виде выборки из N=5000 последовательных отсчетов. Оценим моментные функции данного процесса:

1. Находим выборочное среднее по формуле

где – элементы выборки при , а - размер выборки

Таким образом, .

2. Рассчитываем выборочную дисперсию (в среде Scilab используем функцию corr), используя формулу

где – элементы выборки, – размер выборки

Откуда .

3. Находим корреляционную функцию с помощью следующей формулы:

где - размер выборки;

и нормированную корреляционную функцию, используя формулу:

В работе данная функция вычисляется для 10 отсчетов (для ):

1.0000

0.7484

0.7485

0.8832

0.7048

0.7007

0.7263

0.6445

0.6320

0.6297

0.5810

4. Радиус корреляции случайного процесса вычисляется по формуле

и равен

4. График оценки корреляционной функции будет выглядеть следующим образом (рис. 1)

Рисунок 1 – Нормированная корреляционная функция исходного процесса

2. Модель АР(M) порядков M=1,2,3

Построим модели авторегрессии АР(М)=АРСС(М, 0) порядков . Будем это делать на основе решения системы уравнений Юла-Уокера. Модель авторегрессии имеет вид:

Исходя из известных значений корреляционной функции исходного процесса рассчитаем его модель АР с помощью следующего метода:

Для модели АР(M) численными методами решается нелинейная система М+1 неизвестных:

В зависимости от порядка модели авторегрессии составим системы уравнений, для нахождения коэффициентов :

Для модели АР(1):

Для модели АР(2):

Для модели АР(3):

Найдем неизвестные коэффициенты и с помощью математического пакета Scilab.

Для этого применим функцию AR(rX,N), где параметры - корреляционная функция исходного процесса и порядок модели. Используя функцию fsolve (функция SciLab для решения нелинейных систем уравнений) решаем систему уравнений для модели порядка N, попутно проверяя её существование (если переменная info, которую возвращает fsolve, равна 4, т.е. система не имеет решений).

А также проверяем модель на устойчивость с помощью функции stable(betas). Для M=1 модель устойчива тогда и только тогда, когда , для M=2 модель устойчива тогда и только тогда, когда , для M=3 модель устойчива тогда и только тогда, когда

.

Таким образом, коэффициенты получились равными:

Таблица 1 –Параметры моделей АР

АР(M)	Параметры модели АР
Порядок модели
1
2
3

Для сравнения нормированных корреляционных функций будем использовать критерий среднего квадратичного отклонения по первым десяти отсчётам:

, где – выборочная нормированная корреляционная функция исходного процесса, – рассчитанная теоретическая нормированная корреляционная функция для модели АРСС (M,0).

Таблица 1.1 - Результаты вычисления средне квадратичного отклонения для АР(М)

М
1	2	3

Из таблицы видно, что наилучшей моделью АР(М) является модель АР(3).

3. Модель CC(N) порядков N=0,1,2,3

Построим модели скользящего среднего СС(N)=АРСС(0,N) порядков . Будем это делать на основе решения системы уравнений нелинейных уравнений.

Модель скользящего среднего имеет вид

Исходя из известных значений корреляционной функции исходного процесса рассчитаем его модель CC с помощью решения численными методами системы N+1 неизвестных:

В зависимости от порядка модели скользящего среднего составим системы уравнений, для нахождения коэффициентов :

Для модели СС(0):

Для модели СС(1):

Для модели СС(2):

Для модели СС(3):

Найдем неизвестные коэффициенты с помощью математического пакета Scilab.

Для этого применим функцию MA(rX,N), где параметры - корреляционная функция исходного процесса и порядок модели. В ней мы с помощью функции fsolve (функция SciLab для решения нелинейных систем уравнений) решаем систему уравнений для модели порядка N, попутно проверяя её существование (если переменная info, которую возвращает fsolve, равна 4, т.е. система не имеет решений) Таким образом, коэффициенты получились равными:

Таблица 2 –Параметры моделей СС

СС(N)	Параметры модели
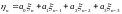
Порядок модели
0
1	не существует
2	не существует
3	не существует

Для сравнения нормированных корреляционных функций будем использовать критерий среднего квадратичного отклонения по первым десяти отсчётам:

, где – выборочная нормированная корреляционная функция исходного процесса, – рассчитанная теоретическая нормированная корреляционная функция для модели АРСС (0,N).

Таблица 2.2 - Результаты вычисления средне квадратичного отклонения для СС(N)

М
0	1	2	3

Наилучшей моделью СС(N) является единственная существующая модель СС(0).

4. Модель АРСС(M,N) порядков M=1,2,3 N=1,2,3

Рассчитаем смешанные модели АРСС(M,N) двумя способами.

Модель авторегрессии скользящего среднего имеет вид

(!)Замечание: блоки уравнений А, Б, В, Г описаны в 5 пункте в таблице 4.

Метод 1

а) Из уравнений блока Б находятся оценки неизвестных параметров

б) Из уравнений блока А, с использованием соотношений блока Г , находятся значения оставшихся параметров

Метод 2

а) Из уравнений блока Б находятся оценки неизвестных параметров

б) С помощью уравнения строим промежуточную последовательность

в) Строится выборочная корреляционная функция промежуточной последовательности

г) Из системы (N+1) нелинейных уравнений

Находятся оценки (N+1) неизвестных коэффициентов

Пример расчетов:

Метод 1

Для модели АРСС(3,3):

Подставляем в систему:

Откуда:

Метод 2

Для модели АРСС(3,3):

Строим промежуточную случайную последовательность с помощью уравнения (в нашем случае m = 3), где значения исходного процесса. Находим оценку корреляционной функции промежуточной последовательности.

Из уравнения:

Находим оценки параметров

Рисунок 2 – Нормированная корреляционная функция промежуточной случайной последовательности, полученной при построении модели АРСС(3,3)

Аналогично находим параметры остальных моделей:

Таблица 3 –Параметры смешанных моделей АРСС

Порядок модели		Параметры модели
M	N
1	1	не существует
1	2	не существует
1	3	не существует
2	1	не существует
2	2	не существует
2	3	не существует
3	1	0.0263 0.0263	0.1878 0.1878	0.7229 0.7229	34.0623 34.1044	7.1807 7.2528
3	2	0.0869 0.0869	0.0839 0.0839	0.7553 0.7553	33.8780 33.9162	4.5886 4.6415	6.1279 6.1869
3	3	0.1920 0.1920	0.2234 0.2234	0.4917 0.4917	25.3709 25.3892	12.2998 12.3828	-9.8045 -9.7920	19.2037 19.1992

Верхние значения в таблице найдены первым способом, нижние вторым.

Определим лучшую модель АРСС (M,N) с помощью средне квадратичного отклонения:

M	N
	1	2	3
1
2
3	0.0182	0.0114	0.0001

Из таблицы видно, что наилучшей моделью АРСС(M,N) является модель АРСС(3,3).