1.5 Ошибки измерений

Численное значение физической величины получается в результате ее измерения, т. е. сравнения ее с другой величиной того же рода, принятой за единицу. При проведении измерений получение точного значения измеряемой величины физически невозможно. Исследователь получает значение величины с некоторым отклонением, называемым ошибкой измерения. Ошибкой измерения называется разность между результатом измерения и истинным значением измеряемой величины. Ошибка измерения обычно неизвестна, как и истинное значение величины. Ошибки измерения имеют разные величины, вызываются разными причинами и классифицируются следующим образом.

Грубые ошибки возникают вследствие нарушения основных условий измерения или в результате недосмотра экспериментатора. При обнаружении грубой ошибки результат измерения следует сразу отбросить, а само измерение повторить (если это возможно). Внешним признаком результата, содержащего грубую ошибку, является его резкое отличие по величине от результатов остальных измерений.

Ошибки измерения вызываются большим количеством разнообразных причин (факторов). Иногда в проведенной серии измерений один из факторов оказывается превалирующим. Например, если после измерений обнаружена неправильная регулировка прибора, которая привела к смещению начала отсчета, то все снятые показания будут смещены либо на постоянную величину, если шкала прибора равномерна, либо на величину, изменяющуюся по определенному закону, если шкала прибора неравномерна. Другим примером может служить изменение внешних условий, например, температуры, если известно влияние этих изменений на результаты измерений.

Принято говорить, что каждая из таких причин вызывает систематическую ошибку. Обнаружение таких ошибок довольно трудозатратно, но результаты измерений легко исправимы.

Ошибки измерения, остающиеся после устранения всех выявленных систематических ошибок, т. е. ошибки результатов измерений, исправленных путем введения соответствующих поправок, называются случайными. Случайные ошибка вызываются большим количеством таких факторов, эффекты действия которых столь незначительны, что их нельзя выделить и учесть в отдельности. Случайную ошибку можно рассматривать как суммарный эффект действия таких факторов.

Случайные ошибки являются неустранимыми, их нельзя исключить в каждом из результатов измерений. Но с помощью методов теории вероятностей можно учесть их влияние на оценку истинного значения измеряемой величины, что позволяет определить значение измеряемой величины со значительно меньшей ошибкой, чем ошибки отдельных измерений.

Для оценки достоверности результатов измерений вводятся в рассмотрение понятия доверительного интервала и доверительной вероятности.

Доверительным называется интервал значений , в который попадает истинное значение измеряемой величины с заданной вероятностью.

Доверительной вероятностью (достоверностью) измерения называется вероятность того, что истинное значение измеряемой величины попадает в данный доверительный интервал, т.е. в зону . Эта величина определяется в долях единицы или в процентах

,

где - интегральная функция Лапласа (Прил. 1).

Интегральная функция Лапласа определяется следующим выражением:

.

Аргументом этой функции является гарантийный коэффициент:

, (10)

где – половина доверительного интервала, .

Если же на основе определенных данных установлена доверительная вероятность (часто ее принимают равной 0.95, 0.99 или 0.999 в зависимости от степени ответственности расчета), то устанавливается точность измерений (доверительный интервал ) на основе соотношения

.

Половина доверительного интервала равна

, (11)

где - аргумент функции Лапласа, если (Прил. 1);

- аргумент функции Стьюдента, если (Прил. 2). В последнем случае, зависит не только от доверительной вероятности, но и от степени свободы .

Таким образом, доверительный интервал характеризует точность измерения данной выборки, а доверительная вероятность ( ) - достоверность измерения.

Значение называют уровнем значимости. Из него следует, что при нормальном законе распределения ошибок погрешность, превышающая доверительный интервал, будет встречаться один раз из измерений, где

.

Это означает, что приходится браковать одно из измерений.

2. ОПРЕДЕЛЕНИЕ ЖЕСТКОСТИ ПРУЖИНЫ И ОЦЕНКА ТОЧНОСТИ МЕТОДА

2.1 Цель работы

Целью работы является определение коэффициента жесткости пружины двумя методами: статическим методом и методом строительной механики, сравнение результатов и оценка погрешностей методов.

При этом студенты получают навыки получения экспериментальных данных и обработки их методами математической статистики.

2.2 Описание лабораторной установки

Лабораторная установка представляет собой двухопорную балку двутаврового сечения с установленной посредине пролета лебедкой подъема (Рис. 2). К крюковой подвеске через пружинную вставку присоединяется груз массой кг.

Значение ускорения свободного падения в технических расчетах принимают м/с².

Модуль упругости стали при сдвиге Н/м².

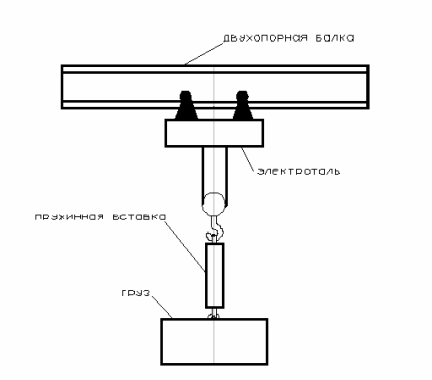
Рис. 2 Схема лабораторной установки.

2.3 Получение исходных данных

Группа разбивается на бригады числом не более 4-х студентов. Каждой бригаде назначается номер пружинной вставки (№=1-4) и количество измерений (n=10-15). По указанию преподавателя бригады поочередно проводят замеры следующих характеристик пружины:

количество витков - ,

внешний диаметр пружины, мм - ,

диаметр прутка пружины, мм - ,

длина пружины в несжатом состоянии, мм - .

Полученные результаты сводят в таблицу.

Таблица 1

Результаты измерений пружины №…

№ п/п		, мм	, мм	, мм	, мм
1
2
…	…	…	…	…	…
n-1
n

Замеры длины пружины проводят с помощью линейки, а внешнего диаметра пружины и диаметра прутка пружины с помощью штангенциркуля (Рис. 3).

Рис. 3 Штангенциркуль

Штангенциркуль, как и другие штангенинструменты (штангенрейсмас, штангенглубиномер), имеет измерительную штангу с основной шкалой и нониус - вспомогательную шкалу для отсчёта долей делений. Точность его измерения – десятые (сотые) доли миллиметра.

В устройство штангенциркуля входят:

1 - штанга; 2 - подвижная рамка; 3 - шкала штанги; 4 - губки для внутренних измерений; 5 - губки для наружных измерений; 6 - линейка глубиномера; 7 - нониус; 8 - винт для зажима рамки.

Измерения с помощью штангенциркуля проводят по шкалам штанги и нониуса:

1) считают число целых миллиметров, для этого находят на шкале штанги штрих, ближайший слева к нулевому штриху нониуса, и запоминают его числовое значение;

2) считают доли миллиметра, для этого на шкале нониуса находят штрих, ближайший к нулевому делению и совпадающий со штрихом шкалы штанги, и умножают его порядковый номер на цену деления (0,1 мм) нониуса.

3) подсчитывают полную величину показания штангенциркуля, для этого складывают число целых миллиметров и долей миллиметра.

Затем, по указанию преподавателя и под его надзором устанавливают пружинную вставку и надежно закрепляют ее. Преподаватель, убедившись в том, что все студенты удалились на безопасное расстояние, поднимает груз и, дождавшись прекращения колебаний, разрешает замеры длины пружины в сжатом состоянии . Результаты замеров также заносятся в таблицу 1.