1.3 Понятие о случайной величине и ее характеристики
Случайная величина — это величина, которая принимает одно из множества значений на некотором интервале с определенной частотой, причём появление того или иного значения этой величины до её измерения нельзя точно предсказать. Частота появления данного значения случайной величины (попадания величины в некоторый интервал) называется вероятностью. Случайные величины могут быть непрерывными, дискретными и смешанными. В дальнейшем рассматриваются только непрерывные величины. Задать случайную величину, описав этим все её вероятностные свойства, как отдельной случайной величины, можно с помощью плотности вероятности (плотности распределения вероятности, закона распределения случайной величины).
Плотностью
распределения (или плотностью вероятности)
непрерывной случайной величины 
в точке 
называется производная ее функции
распределения в этой точке и обозначается
.
График плотности распределения называется
кривой распределения.
Пусть
имеется точка
и прилегающий к ней отрезок 
.
Вероятность попадания случайной величины
на этот интервал равна 
.
Эта величина называется элементом
вероятности.
Вероятность
попадания случайной величины
на произвольный участок 
равна сумме элементарных вероятностей
на этом участке:
.
В
геометрической интерпретации 
равна площади, ограниченной сверху
кривой плотности распределения
и опирающейся на участок (α,β) (Рис. 1).
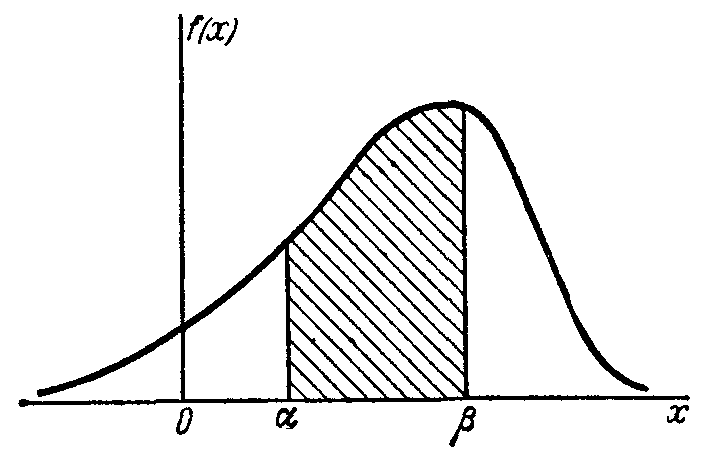
Рис. 1 Кривая плотности распределения.
Свойства плотности вероятности:
Числовые характеристики случайных величин.
В теории вероятностей и математической статистике применяется большое количество различных числовых характеристик, имеющих различное назначение и различные области применения. Среди них характеристики положения, те, которые характеризуют положение случайной величины на числовой оси, т. е. указывают некоторое среднее, ориентировочное значение, около которого группируются все возможные значения случайной величины: математическое ожидание, мода, медиана.
Математическим ожиданием дискретной случайной величины называется сумма произведений всех возможных значений случайной величины на вероятности этих значений
(1)
где
– вероятность появления значения 
,
– количество ожидаемых значений.
Математическим ожиданием непрерывной случайной величины , возможные значения которой принадлежат отрезку , называют определенный интеграл
(2)
Если возможные значения принадлежат всей числовой оси, то
(3)
Кроме характеристик положения - средних, типичных значений случайной величины,-употребляется еще ряд характеристик, каждая из которых описывает то или иное свойство распределения. В качестве таких характеристик чаще всего применяются так называемые моменты. В зависимости от рассмотрения отклонений, квадратов отклонений и более высоких степеней отклонений значений от среднего положения различают моменты второго и более высоких порядков.
Центрированной случайной величиной, соответствующей величине , называется отклонение случайной величины от ее математического ожидания:
Дисперсией случайной величины X называется математическое ожидание квадрата соответствующей центрированной величины
(4)
(5)
Дисперсия случайной величины есть характеристика рассеивания, разбросанности значений случайной величины около ее математического ожидания. Само слово «дисперсия» означает «рассеивание».
Дисперсия случайной величины имеет размерность квадрата случайной величины; для наглядной характеристики рассеивания удобнее пользоваться величиной, размерность которой совпадает с размерностью случайной величины. Для этого из дисперсии извлекают квадратный корень. Полученная величина называется средним квадратическим отклонением (сокращенно, СКО, иначе - «стандартом») случайной величины .
(6)
Третий центральный момент служит для характеристики асимметрии (или «скошенности») распределения и носит название коэффициента асимметрии. Если распределение симметрично относительно математического ожидания (или, в механической интерпретации, масса распределена симметрично относительно центра тяжести), то все моменты нечетного порядка (если они существуют) равны нулю.
Четвертый центральный момент служит для характеристики так называемой «крутости», т. е. островершинности или плосковершинности распределения. Эти свойства распределения описываются с помощью так называемого «эксцесса».