Расширение потока в косом срезе сопла

Сопла обычно бывают наклонены под углом _1п к направлению вращения рабочих лопаток. Вследствие этого концевая часть сопла от расчетного выходного сечения 1-1' (рис. 13) до действительного выходного сечения 1-2 представляет собой так называемый косой срез, который поток должен пройти до входа на рабочие лопатки.

Косой срез начинает работать, если давление за сопловой решеткой Р₁ ниже критического значения Р_кр. В этом случае весь процесс складывается как бы из двух этапов. На первом этапе происходит расширение в собственно сопловом канале, ограниченном четырьмя стенками (до расчетного выходного сечения 1-1’). Здесь давление падает от величины Р₀ до Р_кр, а остальной перепад Р_кр – Р₁ срабатывается в косом срезе.

При этом скорость потока становится сверхзвуковой, а увеличение удельного объема пара (газа) приводит к отклонению потока в косом срезе от осевой линии в сторону открытой части на угол .

Именно эта величина и представляет интерес для дальнейших расчетов. Угол отклонения потока за счет расширения в косом срезе  может быть найден из выражения

–критическая скорость в сечении 1-1’,

–скорость потока на выходе из косого среза,

–потеря энергии в сопловом канале,

–критическое давление.

В реальных условиях работы сопловой решетки угол  не должен быть больше 3  5°.

Расчет сопловых решеток

Цель расчета – определить геометрические размеры сопловой решетки для конкретной турбинной ступени. Это – часть теплового расчета турбины.

Исходные данные:

G – кг/сек – массовый расход рабочего вещества через решетку,

Р₀ – МПа (кгс/см²), давление перед решеткой,

t_{0 –} С – температура перед решеткой,

Р₁, – МПа (кгс/см²) – давление за решеткой,

D_ср – м – средний диаметр облопатывания,

_1п – геометрический угол выходной кромки профиля; принимается в пределах 11  24 °.

Определяется отношение давлений на решетке и выбирается тип сопловой решетки:

–решетка со сходящимися сопловыми каналами,

–решетка со сходящимися сопловыми каналами с расширением в косом срезе,

–решетка с расходящимися сопловыми каналами.

Расчет сопловой решетки со сходящимися сопловыми каналами без расширения в косом срезе

По исходным параметрам начинается построение процесса расширения в тепловой диаграмме (рис. 15) и определяется располагаемый теплоперепад h₀₁, а затем теоретическая скорость истечения м/с

Дальнейший расчет производится в двух приближениях.

Расчет в первом приближении

Ориентировочно оценивается коэффициент потери скорости₁ = 0,96  0,98, а за тем находится действительная скорость истечения c’₁ и потеря энергии на решетке h’_c.

Далее строится действительный процесс 0-1 и в точке 1 снимается удельный объем пара на выходе из решетки \/'₁ м³/кг.

Определяется скорость звука при параметрах выходного сечения м/с и число Маха

В зависимости от принятого угла _1п и получившегося числа М_1t по атласу профилей подбирается подходящий профиль.

Например, С-9015А или С-9018Б.

С – профиль предназначен для сопловых решеток

А – дозвуковая решетка, М  0,9

Б – околозвуковая решетка, М = 0,9  1,2

Первые две цифры соответствуют углу _0п, вторые – _1п.

Для подобранного профиля из атласа берется рекомендуемый относительный шаг и угол установки_у. Далее по графику в зависимости от и_у находится _1эф. График имеет вид, представленный на рис. 16.

Далее определяется высота выходных кромок сопловой решетки

В данной формуле  – степень парциальности впуска – отношение длины дуги, занятой сопловой решеткой, к длине всей окружности ступени на среднем диаметре облопатывания. Первоначально принимается  = 1 и делается расчет. Если < 0,012 м, то делается пересчет: т.е., принимается желательная величина> и пересчитывается, которая будет меньше единицы. Из атласа находится хорда профиля b₁, определяется шаг решетки t₁ = b₁ и отношение .

Расчет во втором приближении

По графикам определяются и

Графики имеют вид, представленный на рис. 17 и 18.

Определяются .

Повторно строится процесс в тепловой диаграмме с учетом нового значения h_c, снимается величина удельного объема и находится высота выходных кромок решетки во втором приближении

Число сопловых каналов .

Полученная цифра округляется до ближайшего целого значения; если при этом  < 1 то пересчитывается . Если же  = 1, то после округления z_c – пересчет t₁. Все остальное – без изменений.

Расчет сопловой решетки со сходящимися сопловыми каналами с расширением в косом срезе

При наличии расширения в косом срезе в минимальном сечении скорость течения будет равна скорости звука, а давление – критическому. Определяется критическое давление.

По исходным данным строится теоретический процесс в тепловой диаграмме (рис. 19), откуда снимаются полный располагаемый теплоперепад h₀₁ и теплоперепад, соответствующий критическому перепаду давлений h_0кр.

Определяется полная теоретическая скорость истечения . Принимается коэффициент и оценивается потеря энергии в соплах h_c. По результатам построения определяется удельный объем в минимальном сечении \/_к м³/кг и критическая скорость . Оценивается число Маха.

В зависимости от принятого _1п по атласу подбирается профиль из группы Б, находится и_у , а затем по графику и подсчитывается высота выходных кромок:

Если < 0,012 м, то производится пересчет по аналогии с предыдущим вариантом.

Определяется шаг сопловой решетки t₁ и число сопловых каналов. Расчет во втором приближении, как правило, не производится из-за очень небольшой разницы в результатах.

Преобразование энергии на рабочих лопатках

Выходящий из сопел пар (газ) попадает в каналы, образованные рабочими лопатками, и здесь происходит второе преобразование: кинетическая энергия потока превращается в механическую работу вращения рабочего колеса. При обтекании потоком профилей рабочих лопаток на каждой из них возникает подъемная сила, приводящая в движение рабочее колесо турбины. Силу Р_z, действующую на каждой лопатке, можно разложить на две составляющие: Р_uz – окружную и Р_az – осевую (рис. 20)

Величина работы, развиваемой колесом, будет определяться только окружными составляющими Р_u (окружной силой).

Как полная сила Р_z, действующая на лопатку, так и её составляющие, могут быть легко найдены, если применить к каналу, ограниченному двумя соседними рабочими лопатками, известный из механики закон количества движения. Примем следующие обозначения:

G – кг/с – массовый расход рабочего вещества через решетку,

z – количество каналов, через которые этот поток движется,

c₁ – м/с – абсолютная скорость потока при входе в канал,

c₂ – м/с – то же, при выходе из канала,

dt – сек – произвольный промежуток времени.

Тогда элементарная масса, входящая в канал и выходящая из него за этот промежуток времени

(рис. 21)

По закону количества движения т.е., изменение количества движения за какой-то промежуток времени равно импульсу силы за тот же промежуток времени.

Здесь Р’_z – сила, с которой стенки канала действуют на поток, заставляя его изменять направление движения.

Согласно закона Ньютона сила, с которой поток будет действовать на стенки канала, P_z, равна P’_z, но противоположна по знаку, т.е., Р’_z = – Р_z. В результате можно записать

или

После преобразований .

По аналогии и.

При этом следует помнить, что в скобках находятся проекции векторов скорости и поэтому, подставляя вместо c_1u и c_2u их значения, следует учитывать не только величину, но и направление этих составляющих скоростей.

Если c_1u и c_2u направлены в разные стороны (как это чаще всего бывает), то их абсолютные значения следует сложить, и наоборот, если они направлены в одну сторону, вычесть одно из другого (рис. 22).

Для всего рабочего колеса турбины при числе лопаток z окружное усилие определится так:

н/кг (м/сек²)

Секундная работа потока (т.е., мощность)

Вт (нм/с или Дж/с)

Мощность, отнесенная к массе в 1 кг

Вт/кг (Дж/(cкг))

Подобным же образом можно вывести выражение для определения осевой силы

н

Выражения для определения P_u и Р_a носят название уравнений Эйлера в честь академика, впервые получившего их в 1754 году.

Степень реакции турбинной ступени

Степенью реакции турбинной ступени называется отношение располагаемого теплоперепада, приходящегося на рабочую решетку, ко всему теплоперепаду, приходящемуся на ступень

Для ступени активного типа

Для ступени с реакцией

Оптимальная форма профиля рабочих лопаток

Форма профиля, в основном, определяется его геометрическими углами _1п и _2п их соотношением. Исходные уравнения

и

Наивыгоднейший профиль будет такой, у которого возникающая на нем сила Р будет иметь окружное направление, т.е., если Р = Р_u,а Р_а = 0. При этом P_u имеет наибольшее возможное значение, и совершаемая работа будет максимальной.

Для преобразования исходных уравнений воспользуемся так называемыми "треугольниками скоростей" (рис. 24), которые дают взаимосвязь между абсолютными и относительными скоростями потока и окружной скоростью на входной и выходной кромках профиля. Треугольники скоростей позволяют определить окружные и осевые составляющие каждого вектора скорости.

Примем, что составляющие векторов, направленные по ходу вращения, имеют знак "плюс" (+), а против направления вращения – знак "минус" (-).

В результате, по треугольникам скоростей получаем:

Тогда

Связь между составляющими векторами относительных скоростей потока на входе и выходе с рабочей решетки дана на рис. 25.

Отсюда

Оптимальный профиль при активном типе облопатывания

В каналах между рабочими лопатками в этом случае давление постоянно и, следовательно, относительная скорость, если не учитывать потери, должна быть постоянной, т.е., .

Тогда

Отсюда следует, что должно быть илит.е., профиль лопатки должен быть симметричным. В действительности же из-за потерь

Вследствие этого, как видно из выражения для определения P_u, эта сила будет меньше, чем при отсутствии потерь. Желательно, чтобы сила P_u была по возможности большей. Это может быть в известной степени достигнуто за счет уменьшения угла _2п по сравнению с _1п.

При уменьшении _2п увеличивается cos , а следовательно и сила P_u. По этим соображениям угол _2п принимается на 3  5  меньше _1п.

При этом сила P_u при наличии сопротивлений примерно равна силе P_u, при отсутствии сопротивлений, но появляется сила P_a > 0, с чем приходится мириться.

Вывод: в активной турбинной ступени профили рабочих лопаток должны быть близкими к симметричной форме.

Оптимальный профиль при наличии реакции в ступени

При наличии реакции в ступени в межлопаточных каналах происходит дополнительное расширение потока, давление падает, а относительная скорость нарастает. В результате W₂ > W₁.

Для обеспечения Р_a = 0, выражение и стоящее в скобках, должно быть равно 0, т.е.,

или

Так как , тоsin _1п > sin _2п т.е. _1п > _2п

Вывод: в турбинной ступени с реакцией профили рабочих лопаток должны быть резко несимметричными.

Потери на рабочих решетках

Коэффициент потери энергии на лопатках _л и скоростной коэффициент .

Потери на рабочей решетке, так же, как и на сопловой , зависят от большого количества факторов: от формы профиля рабочих лопаток, угла поворота струи на рабочих лопатках, угла установки профиля, шага решетки, хорды профиля и высоты канала, скорости потока и т.д.

Потери на рабочей решетке так же могут быть разделены на две основные группы:

1. Профильные потери

а). трения в пограничном слое,

б). вихревые потери при отрывах потока на профиле,

в). кромочные потери,

г). потери в скачках уплотнения.

2. Концевые потери

а). потери трения в пограничном слое у торцевых стенок,

б). потери вследствие вторичных токов,

в).потери от взаимодействия струи с неподвижным паром (газом) в зазоре между сопловой и рабочей решетками.

Природа потерь на рабочей решетке такова же, что и на сопловой решетке.

Потери трения в пограничном слое зависят в первую очередь от характера пограничного слоя и, соответственно, от числа Маха.

₂ – кинематическая вязкость,

W₂ – скорость потока на выходе из канала,

b₂ – хорда профиля.

Оптимальное значение числа Рейнольдса Re_л = 1,510⁵  410⁵.

Вихревые потери при отрывах потока на профиле

В отличие от сопловых решеток данная потеря на рабочих лопатках может возникать довольно часто и оказывает значительное влияние на общую величину потерь – как профильных, так и концевых. Отрыву потока на входной кромке профиля предшествует явление удара либо в спинку профиля, либо в его рабочую часть

Основной фактор здесь – разность углов ₁ – _1п.

Если ₁ – _1п > 0, т.е., положительна, то имеет место удар в спинку профиля.

Если же ₁ – _1п < 0 – (отрицательна) – удар в рабочую поверхность.

Влияние удара на профильные и концевые потери учитывается отдельными коэффициентами В_пр и В’_кон, характер которых представляется графиками (рис. 27 и 28).

Кромочные потери

Коэффициент кромочных потерь К = 0,1 0,3

а’_л – ширина канала в выходном сечении;

₂ – толщина выходной кромки.

Потери в скачках уплотнения

Оцениваются коэффициентом _волн

Общая оценка профильных потерь

Потери трения в пограничном слое у торцевых стенок канала и потери вследствие вторичных токов

Данные потери оцениваются по аналогии с такими же потерями на сопловых решетках.

Потери от взаимодействия потока с неподвижным рабочим веществом в зазорах (потери от подсоса)

Подсасываемый пар (газ) (см. рис. 29), смешиваясь с основным потоком, создает зоны завихрения у торцевых стенок канала и, как следствие, потерю энергии.

Учет подсоса производится с помощью поправочного коэффициента В который может быть определен по графику из атласа профилей. Вид графика дан на рис. 30.

В результате

Полный коэффициент потери энергии на рабочей решетке:

Для более точной оценки потерь энергии на рабочей решетке могут быть учтены дополнительные факторы:

1. наличие бандажной ленты,

2. наличие угла раскрытия проточной части

Вид соответствующих графиков дан на рис. 31 и 32б

В результате

Треугольники скоростей турбинной ступени

Усилия, работа и мощность на венце рабочих лопаток – функция скоростей движения потока в межлопаточных каналах. Для расчета ступени и нахождения интересующих нас скоростей удобно пользоваться треугольниками скоростей. Их два – входной треугольник, дающий взаимосвязь скоростей на входной кромке профиля, и выходной – на выходной кромке (рис. 33).

Р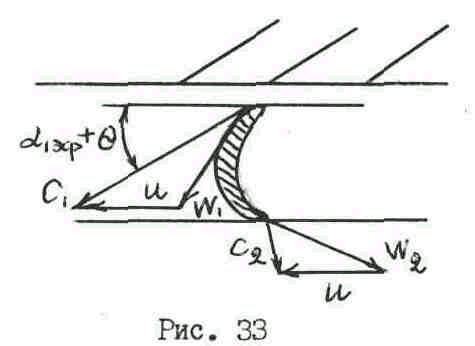ассмотрим порядок построения треугольников скоростей при наличии реакции в турбинной ступени.

Должны быть заданы параметры пара Р₀, t₀, P₂ и степень реакции  .

В тепловой диаграмме строится процесс расширения рабочего вещества (рис. 34) и производится расчет сопловой решетки, откуда получаются значения c₁, _1эф и  (если имеет место расширение в косом срезе сопла).

Основные зависимости:

Далее на базовой линии Х-Х (рис. 35) от исходной точки 0 под углом в масштабе (в 1 см – х м/сек) откладывается вектор с₁ (все прочие вектора откладываются в том же масштабе). Определяется окружная скорость

n – об/мин – число оборотов ротора,

D_ср – средний диаметр облопатывания.

Вектор u пристраивается параллельно базовой линии к концу вектора c₁. При соединении точки 0 с другим концом вектора u получается вектор относительной скорости входа потока на рабочую решетку W₁ и относительный угол входа ₁.

Предварительно оценивается коэффициент  и находится относительная скорость потока на выходе с рабочих лопаток и её теоретическое значение.

Определяется потеря энергии на рабочей решетке и после откладывания её на построении процесса, снимается удельный объем \/₂ м³/кг (рис. 34). Критическая скорость при параметрах выходного сечения м/сек; соответствующее число Маха

Через выражение определяется угол₂.

Далее по углам ₁, ₂ и числу Маха М_2t из атласа подбирается стандартный профиль и по графику находится _2эф (по аналогии с сопловой решеткой).

При малом различии углов ₁ и ₂ профиль подбирается из группы Р, например Р-3021А. Буква Р обозначает, что профиль предназначен для рабочих решеток; первая пара цифр соответствует углу _1п, вторая – _2п, а последняя буква – характеру истечения.

Если же углы ₁ и ₂ различаются значительно, то профиль подбирается из группы С, например С-9015А. В этом случае первая пара цифр соответствует углу _1п, а вторая – _2п.

Профиль в обоих случаях нужно подбирать так, чтобы было максимальное соответствие углов: ₂ по расчету и _2п.

Если в подобранном профиле при этом будет значительное различие угла _1п с углом ₁ по построению, что приводит к появлению удара на входной кромке, то данное обстоятельство должно быть учтено при дальнейших расчетах.

Под углом _2эф от базовой линии откладывается вектор W₂, к нему пристраивается вектор u и проводится замыкающий вектор c₂ – вектор абсолютной скорости потока при выходе с рабочей решетки. Построив треугольники скоростей можно снять все интересующие нас составляющие.

Следует отметить, что если  = 0,5, то c₁  W₂; W₁  c₂; _1эф  _2эф; ₁  ₂.

Построение процесса расширения в ступени в тепловой диаграмме

При построении процесса в тепловой диаграмме (рис. 36) прежде всего должны быть учтены три основные потери энергии:

потеря в соплах

потеря на рабочих лопатках

потеря с выходной скоростью – при выходе потока из каналов рабочей решетки

Величина именуется окружным теплоперепадом.

Расчет рабочих решеток

Цель расчета – определить геометрические размеры рабочей решетки к уже рассчитанной сопловой решетке и построить профиль проточной части.

Исходные данные G, Р₀, t₀, D_ср – те же, что и для сопловой решетки.

Давление за рабочей решеткой Р₂ задается дополнительно.

 – из расчета сопловой решетки; степень реакции  задается.

Расчет производится в двух приближениях.

Расчет в первом приближении

Предварительно оценивается скоростной коэффициент для рабочей решетки ’, строится процесс в тепловой диаграмме и треугольники скоростей; при этом подбирается стандартный профиль.

После этого определяется высота выходных кромок рабочей решетки

Из атласа находится хорда профиля b₂, определяется шаг решетки , отношение и ширина решётки В₂.

По графикам определяются и

Находятся и

Далее уточняется м/с и

По уточненному значению h_л на тепловой диаграмме снимается \/₂ и определяется

Находится число лопаток в решетке с округлением до ближайшего целого.

Строится профиль проточной части (рис. 37).

Ориентировочное значение величины перекрышей, мм
50	1,5 – 2.5
100	2,5 – 3,5
200	3,5 – 4,5

Окружной КПД турбинной ступени (относительный КПД на лопатках)

Окружным КПД турбинной ступени называется отношение полезной энергии одного кг рабочего вещества W₁ к располагаемой энергии W₀.

Исследование данного выражения позволяет выяснить условия, необходимые для получения наиболее высокого КПД, т.е., позволяет решить наиболее существенную проблему в расчете турбинной ступени.

1. Окружной КПД активной турбинной ступени

На основании ранее сделанных выкладок Вт/кг

При условии, что весь располагаемый теплоперепад срабатывается в соплах (активная турбинная ступень)

Вт/кг

тогда

Приведем данное выражение к виду, удобному для исследования.

Ранее было получено .

Для активной турбинной ступени

тогда ,; из треугольника скоростей , т.е.в результате

После подстановки в формулу для определения окружного КПД получаем

Преобразуем эту формулу, используя соотношение и введя выражение

Из полученного выражения следует, что окружной КПД зависит от следующих факторов:

1. от величины потерь энергии в соплах и на рабочих лопатках, характеризуемых коэффициентами  и ,

2. от угла, ₁ – чем меньше этот угол, тем больше КПД,

3. от соотношения углов ₁, и ₂; этот вопрос был рассмотрен ранее,

4. от отношения

Величина Х₁ называется характеристикой турбинной ступени или характеристическим коэффициентом или коэффициентом быстроходности.

Рассмотрим влияние X₁ на величину окружного КПД.

1. _u = 0, если , т.е., еслиu = 0.

Этот случай соответствует заторможенному рабочему колесу, через решетку которого движется поток. В случае идеального течения (без потерь скорости) вся кинетическая энергия потока будет теряться с выходной скоростью c₂ на выходе с рабочих лопаток, c₂ = c₁.

2. _u = 0. если cos ₁ – Х₁ = О, т.е., ;;

Если ₁ = 0 (идеальный, теоретический случай), то X₁=1.

Данный идеализированный случай соответствует проходу рабочего вещества через уже раскрученное колесо, и поток, в относительном движении, пролетает через межлопаточные каналы перпендикулярно направлению вращения (рис. 39).

При  = 1 входной и выходной треугольники скоростей – накладываются друг на друга, с₂ = с₁ т.е., о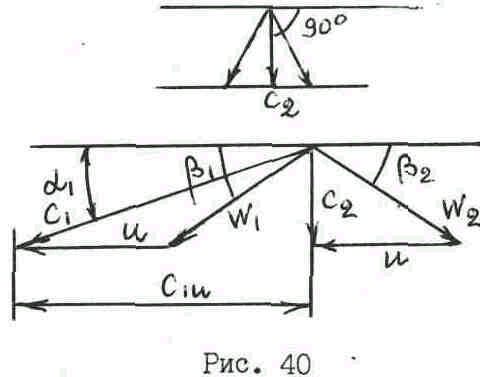пять вся кинетическая энергия потока теряется с выходной скоростью.

В обоих рассмотренных случаях вся энергия потока теряется на выходе с решетки рабочих лопаток, т.е., с выходной скоростью с₂.

Таким образом, характеристика турбинной ступени X₁ связана с потерей энергии с выходной скоростью.

Наивыгоднейшая характеристика будет тогда, когда потеря с выходной скоростью будет наименьшей, а это возможно, когда вектор скорости с₂ перпендикулярен вектору окружной скорости u.

3. Определение оптимальной характеристики X₁, соответствующей наибольшему окружному КПД.

Принимаем идеализированный случай, когда ₁ = ₂,  = 1, тогда W₁ = W₂.

Исходя из этих условий строим треугольники скоростей (рис. 40), из которых следует, что наивыгоднейшее соотношение или.

Отсюда.

При этом окружной КПД будет максимальным.

Если ₁ =0 Х_1опт = 0,5

при ₁ > 0 Х_1опт  0.47  0,48

Характер зависимости _u от Х₁ дан на графике рис. 41.

Вывод: для активной турбинной ступени наивыгоднейшее значение характеристики соответствует примерно 0,5; всякое отклонение характеристики от этого значения в большую или меньшую сторону заведомо даст снижение КПД.

Окружной КПД реактивной турбинной ступени

В случае реактивной турбинной ступени для _u получается иное выражение.

Полезная работа 1 кг пара (газа) определяется так же, как и для активной турбинной ступени

а располагаемая складывается из двух составляющих: кинетической энергии на выходе из сопловых каналов и дополнительного приращения кинетической энергии за счет расширения на рабочей решетке

Рассмотрим случай, когда  =0,5.

При этом c₁ = W₂; c_1t = W_2t; W₁ = c₂; ₁ = ₂;  = .

Сделав подстановку в выражение , произведя соответствующие замены и преобразования, а также введя функцию Х₁ получим

Рассмотрим влияние характеристики Х₁ на величину окружного КПД для данного типа ступени.

1. _u = 0, если Х₁ = 0, т.е. u = 0 – случай, аналогичный рассмотренному в активном варианте ступени.

2. _u =0, если т.е., если Х₁ = 2cos ₁

Соответствует движению рабочего вещества через уже раскрученное колесо. При этом, если ₁ = 0, X₁ =2,

₁ > 0, Х₁  1,9  1,96

В обоих вариантах вся энергия потока теряется на выходе с решетки рабочих лопаток.

3. Наибольший окружной КПД _{u max} – при оптимальной характеристике.

В данном случае потеря с выходной скоростью, при прочих равных условиях, должна быть наименьшей, а это соответствует перпендикулярности вектора c₂ к вектору u.

Построим треугольники скоростей (рис. 41), соблюдая данное условие и принятые выше соотношения углов и скоростей,

Сквозного пролета потока через рабочую решетку не будет, т.к. профили лопаток имеют большую несимметричность.

Из построения u = c_1u = c₁cos ₁; .

При ₁ = 0 Х₁ = 1

₁ > 0 X₁  0,96  0.97

Характер зависимости _u от X₁ дан на графике (рис. 42)

Вывод: для турбинной ступени со степенью реакции  = 0,5 наивыгоднейшее значение характеристики соответствует  1; при этом обеспечивается наивысший окружной КПД.

Для ступеней с промежуточной степенью реакции (от 0 до 0,5) оптимальное значение характеристики дано в таблице I.

Таблица 1.
	0	0.1	0,2	0.3	0,4	0,5
	0,48	0,55	0,63	0.72	0,83	0,96

Рассмотренные выше формулы определения _u неудобны для практического использования. Поэтому в реальных условиях окружной КПД определяется следующим образом:

где h₀ – в кДж/кг

В ряде случаев при производстве тепловых расчетов пользуются "условной характеристикой" где– условная абсолютная скорость, определяемая по полному располагаемому теплоперепаду, приходящемуся на ступень. Соответствующие величины даны в таблице 2.

Таблица 2
	0	0,05	0,1	0,15	0,2	0,25	0,3
	0,47	0,484	0,498	0,512	0,525	0,54	0,554
	0,35	0,4	0,45	0,5	0,55
	0,568	0,582	0,595	0,61	0,624

Турбины со ступенями скорости и многоступенчатые турбины

Общие положения

Максимальный КПД турбинной ступени получается при определенном значении отношения . Всякое отклонение этой характеристики от её значения, соответствующего максимальному_u, снижает этот последний и снижает весьма резко.

Применяемые в настоящее время в паротурбинных агрегатах начальные параметры пара порядка 9  13  24 МПа и температуре 535  565 C и давлении в конденсаторе 0,003  0,005 МПа позволяют иметь в турбинах располагаемые теплоперепады до 1500  1700 кДж/кг.

Если принять простейшую одноступенчатую турбину, то при этом теоретическая скорость истечения пара из сопел, соответствующая принятому расширению, будет равна:

активная ступень,  = 0; с₁ > 1700 м/с,

реактивная ступень,  = 0,5; c₁ > 1200 м/с.

Приняв для активной ступени , а для реактивной, получим необходимые для получения наивысшего КПД значения окружной скорости: активный вариантu > 850 м/с; реактивный – u > 1200 м/с.

Аналогичное явление имеет место и в газовых турбинах.

Современное состояние турбостроительной промышленности не в состоянии обеспечить прочность ротора при таких больших окружных скоростях.

В современных турбинах предельные значения окружных скоростей для роторов дискового типа в области высоких температур составляют порядка 200  250 м/с, а на последних ступенях  400 м/с (на среднем диаметре облопатывания).

В газовых турбинах предельное значение окружной скорости на среднем диаметре  325 м/с.

Следовательно, в простейших активных и реактивных турбинах мы или не будем в состоянии использовать достижения современной теплотехники по параметрам пара, работая на низких располагаемых теплоперепадах, или не сможем достичь сколько-нибудь удовлетворительных КПД.

Турбины со ступенями скорости

Одним из мероприятий, увеличивающих КПД турбины при недостаточно больших окружных скоростях и дающих возможность перерабатывать при этом большие теплоперепады с высоким КПД, является применение ступеней скорости.

Если в случае активной турбины в одной ступени срабатывается большой располагаемый теплоперепад, то пар выходит из сопел с огромной скоростью, значительно превышающей критическую. Так как окружная скорость рабочего колеса мала по сравнению со скоростью пара, то пар будет выходить из каналов рабочей решетки с достаточно большой скоростью c’₂.

Если этот пар со скоростью c'₂ направить на направляющие лопатки, а затем вновь на второй венец рабочих лопаток, укрепленных на том же диске, то на выходе из второго венца рабочих лопаток скорость c''₂ будет уже значительно меньше. Часть кинетической энергии пара будет отдана рабочим лопаткам второго венца и КПД подобной турбины при той же окружной скорости на лопатках значительно возрастет.

Далее пар (или газ) может быть направлен в следующий ряд направляющих, а затем рабочих лопаток; это даст дополнительное срабатывание кинетической энергии и соответствующее повышение КПД турбины.

Таким образом, получаем колесо или ступень давления с двумя или тремя ступенями скорости (в зависимости от числа венцов рабочих лопаток на колесе).

Схема проточной части колеса с двумя ступенями скорости дана на рис. 43. Здесь же показана привязка треугольников скоростей и их индексация.

Соответствующие коэффициенты потери скорости в соплах и на лопаточных венцах обозначим , _л, _н, _л2.

Цифровые индексы на векторах и углах соответствуют номерам кромки и венца рабочих лопаток:

первая цифра – № кромки; 1 – входная, 2 – выходная,

вторая цифра – № венца рабочих лопаток (1-й или 2-й).

Принимая чисто активный вариант турбинной ступени получаем основные зависимости:

; ;;.

Далее установим условия получения наивысшего КПД в зависимости от числа венцов рабочих лопаток.

Так как влияние потерь энергии в соплах и на лопаточных венцах на величину КПД очевидно, то для упрощения задачи примем . Кроме того, примем симметричные профили рабочих и направляющих лопаток, т.е. ₁₁ = ₂₁; ₂₁ = ₁₂; ₂₁ = ₂₂.

Располагаемая энергия (при  = 1) .

Полезная энергия , гдеc_2m – абсолютная выходная скорость в общем случае из последнего венца рабочих лопаток, т.е., m – число венцов рабочих лопаток (или № последнего венца).

Сделав ряд преобразований по аналогии с ранее рассмотренными случаями, получаем

.

Соответственно

1. _u = 0 при X₁ = 0

2. _u = 0 при ;

При ₁ = 0 m = 2, Х₁  0,5

m = 3, Х₁  0,33

3. _u будет максимальным, если вектор скорости c_2m перпендикулярен вектору окружной скорости u.

Тогда ;;

При ₁ = 0 m = 2, Х_1опт  0,25

m = 3; Х_1опт  0,165

Характер зависимости _u от X₁ дан на рис. 44.

Уровень оптимальной окружной скорости при различных типах облопатывания дан в таблице 3.

Таблица 3
		u
Реактивная ступень  = 0,5	1	u = c1
Активная ступень 0 = 0	0,5	u = 0,5c1
Ступень с венцами скорости
m = 2	0,25	u = 0,25c1
m = 3	0,165	u = 0,165c1

т.е., в турбине со ступенями скорости для получения наивысшего КПД окружная скорость должна быть гораздо меньше, чем в ступенях одновенечных при одном и том же располагаемом теплоперепаде.

Полученные результаты дают лишь основные характерные особенности колес со ступенями скорости, но для практических расчетов могут быть использованы с большой, осторожностью, т.к. на них весьма большое влияние оказывают потери течения через проточную часть, которыми мы при этом выводе пренебрегли.

Эти потери очень сильно снижают максимальный КПД такой ступени и тем больше, чем больше число ступеней скорости. Поэтому турбины такого типа выполняют чаще всего с двумя рабочими венцами и реже – с тремя.

Вывести формулу для определения окружного КПД с учетом потерь во всех элементах проточной части можно, но она была бы столь сложна, что пользование ею было бы очень неудобно. Поэтому значительно проще определить окружной в КПД, вычислив окружной теплоперепад турбины

Для двухвенечного колеса

При активном типе облопатывания потери энергии определяются по формулам, приведенным ниже, а построение процесса в тепловой диаграмме дано на рис. 45.

Потери в соплах

потери на 1-ом венце рабочих лопаток

потери на направляющих лопатках

потери на 2-ом венце рабочих лопаток

потеря с выходной скоростью

Окружной КПД так же может быть найден из выражения

h₀ – в кДж/кг

Ступени с венцами скорости часто выполняются с небольшой степенью реакции на рабочих и направляющем венцах. При производстве расчётов эта величина обычно задается  = _л1 + _н + _л2 = 0,1  0,12.

Далее определяются располагаемые теплоперепады, приходящиеся на каждый венец

; ;

; ;

скорости потока и потери энергии по венцам. Строится процесс расширения пара (рис. 46) и треугольники скоростей (рис. 47). Соответствующие зависимости даны ниже.

W₁₁ – из построения

c₂₁ – из построения

W₁₂ – из построения

с₂₂ – из построения

Многоступенчатые турбины

При очень больших располагаемых теплоперепадах, которые обеспечиваются современными параметрами пара, ступени с венцами скорости не могут обеспечить достаточно высокий КПД.

Еще одно мероприятие, наиболее распространенное в современных турбинах и имеющее целью обеспечить наивысший КПД, заключается в том, что в целях сохранения наивыгоднейшей характеристики X₁ при умеренных окружных скоростях, снижают скорости пара на выходе из сопел с₁. Это можно осуществить ступенчатым расширением пара (газа) последовательно в нескольких простейших турбинах, расположенных одна за другой.

Принимая оптимальное значение X₁ и приемлемую окружную скорость u из соотношения находим скорость истечения из сопелc₁, а по ней оцениваем нужный теплоперепад, приходящийся на эту простейшую турбину. Совокупность таких последовательно расположенных простейших турбин носит название многоступенчатой турбины со ступенями давления. Сами простейшие турбины называются ступенями давления многоступенчатой турбины.

Каждая из ступеней давления состоит из соплового аппарата и рабочих лопаток. Все ступени в простейшем случае размещаются в одном корпусе и имеют общий ротор. Такие турбины могут быть как активного, так и реактивного типа.

Иногда ступени с венцами скорости и ступени давления применяются одновременно. Обычно, в этом случае первая ступень многоступенчатой турбины выполняется в виде колеса с венцами скорости, а остальные ступени делаются одно венечными, активными или реактивными.

Основные положения, касающиеся паровых многоступенчатых турбин, в полной мере относятся и к газовым турбинам. Хотя в газовых турбинах располагаемый теплоперепад значительно меньше, чем в паровых, тем не менее и здесь возникает необходимость применения многоступенчатого варианта.

Особенности работы многоступенчатых турбин

Многоступенчатые турбины имеют некоторые особенности работы, отсутствующие у турбин одноступенчатых.

1. Использование скоростной энергии выхода потока из предыдущей ступени при входе в последующую.

Выходя из межлопаточных каналов предыдущей ступени поток имеет какую-то абсолютную скорость выхода с_2пр (рис. 48) и обладает определенным запасом кинетической энергии .

Эта кинетическая энергия добавляется к той, которая получается в сопловых каналах последующей ступени за счет перепада давлении Р₀ – Р₁.

В результате, скорость потока на выходе из сопловой решетки последующей ступени будет функцией двух факторов с₁ = f(P₀ – P₁; c_2пр) т.е., увеличивается по сравнению с вариантом, когда скорость с₁ определяется только по теплоперепаду, обусловленному перепадом давлений.

Для полного использования выходной энергии предыдущей ступени необходимо, чтобы вход потока в сопловые каналы последующей был плавным, безударным. Если же это не обеспечивается, то часть кинетической энергии в результате удара о входную кромку сопловых перегородок и возникающих завихрений превращается в тепловую.

В реальных условиях во многих случаях удается использовать только часть выходной кинетической энергии предыдущей ступени , где – коэффициент использования выходной энергии, а остальная её часть превращается в тепло.

В идеальных условиях при хорошо спроектированной проточной части  = 1. Иногда же, при определенной конфигурации проточной части, сохранить скорость потока с_2пр и его направление не удается; тогда  = 0.

Использование выходной энергии предыдущей ступени невозможно ( = 0) в следующих случаях:

1. в первой ступени турбины; если турбина многокорпусная, то в первой ступени каждого корпуса;

2. в активных ступенях, имеющих парциальный впуск пара, если степень парциальности увеличивается от ступени к ступени;

3. во всех ступенях, идущих вслед за большим скачком среднего диаметра облопатывания;

4. в ступенях, перед которыми имеется большой аксиальный зазор, используемый для отбора пара или же впуска пара в турбину извне.

В общем случае  = 0,5.

Располагаемый теплоперепад данной ступени с учетом использования выходной энергии предыдущей определится из выражения

а построение процесса (для активной ступени) дано на рис. 49.

Получая приращение располагаемой энергии, рассматриваемая ступень, однако, теряет свою выходную энергию – как в виде кинетической, так и тепловой.

Все изложенное выше относительно использования выходной энергии одинаково относится как к активным, так и реактивным многоступенчатым турбинам.

2. "Возвращенное" тепло в многоступенчатых турбинах

Как известно, изобары на диаграмме h – s не параллельны друг другу а расходятся в сторону увеличения энтропии (рис. 50).

Поэтому располагаемый теплоперепад между двумя одними и теми же изобарами при сдвиге действительного процесса вправо от основной адиабаты увеличивается. В результате, сумма располагаемых теплоперепадов отдельных ступеней всегда больше располагаемого теплоперепада турбины в целом.

; и т.д.

т.е.

Увеличение фактического располагаемого теплоперепа­да оценивается "коэффициентом возвращенного тепла" R.

Оценка коэффициента возвращенного тепла для уже построенных паровых турбин показывает, что R = 1,03  1,08.

Данный коэффициент увеличивается:

1. с увеличением степени расширения в турбине,

2. с увеличением потерь энергии в отдельных ступенях турбины, т.е. со снижением КПД турбины,

3. с увеличением числа ступеней в турбине,

4.с увеличением начального давления пара.

3. Характеристический коэффициент (характеристика) многоступенчатой турбины

В многоступенчатых турбинах, так же, как и в одноступенчатых, существует зависимость КПД от соотношения скоростей, но она значительно сложнее.

Соответствующие выражения были предложены двумя различными авторами и носят их имя:

Характеристика Стодола

Характеристика Парсонса

В этих выражениях в числителе – сумма квадратов окружных скоростей на среднем диаметре облопатывания всех ступеней (от 1 до n).

В знаменателе – общий располагаемый теплоперепад, определяющий скорости истечения пара с поправкой на реальность процесса (R).

Характеристика Стодола – это осредненная величина характеристики всех ступеней данной турбины.

Таким образом, характеристика X₁ многоступенчатой турбины связана с характеристиками отдельных ступеней турбины и, следовательно, с КПД всей турбины в целом

В зависимости от степени реактивности ступеней существует наивыгоднейшее значение характеристик X₁ и X, обеспечивающее наивысший КПД.

Данные коэффициенты позволяют ориентировочно судить о степени совершенства турбины.

Далее, если необходимо спроектировать турбину с наивысшим КПД, для которой заданы параметры пара и осредненная степень реакции по ступеням, то принимая оптимальную характеристику Х₁ можно найти значение , а следовательно, при некотором выбранном значении средней окружной скоростиu и нужное число ступеней в турбине.

И еще, если две турбины примерно одинаковой мощности и одинаковой осредненной степени реакции в ступенях, имеют одинаковые характеристики, то, независимо от числа ступеней в этих турбинах и окружных скоростей, их окружные КПД будут равны. При этом распределение теплоперепадов между ступенями не имеет значения.

Общие выводы по многоступенчатым турбинам

Применение многоступенчатых турбин приводит к повышению их КПД по следующим причинам:

1. В каждой ступени может быть выдержано наивыгоднейшее значение характеристики X₁, обеспечивающее получение максимального окружного КПД,

2. Небольшие теплоперепады в каждой ступени позволяют применять сходящиеся сопла, имеющие меньшие потери, более простые в технологическом отношении и работающие устойчиво на переменных режимах,

3. Выходная скорость из каждой ступени (кроме последней) не является потерянной, а может быть использована в последующей ступени, повышая тем самым общий КПД турбины,

4. Наличие потерь энергии в данной ступени частично компенсируется увеличением действительных располагаемых теплоперепадов следующих ступеней за счет "возвращенного тепла", что также повышает общий КПД турбины.

Осевые усилия, действующие в проточной части многоступенчатой турбины

Осевые усилия, действующие в проточной части многоступенчатой турбины, слагаются из двух составляющих:

1. от динамического воздействия потока на рабочие лопатки,

2. от статической разности давление при наличии реакции.

Первая составляющая н; G – кг/сек

Вторая составляющая н;

где давление до рабочей решетки Р₁ и после нее Р₂ – в МПа,

шаг решетки t₂ и высота лопатки – в м,

число лопаток в венце – z₂

общее число ступеней – n

Потери энергии в турбоагрегатах

Все потери энергии, возникающие в турбоагрегате, могут быть разделены на две основные группы: внутренние и внешние.

Внутренние – потери, имеющие место внутри турбинных корпусов и влияющие на количество и качество (состояние) протекающего в турбине рабочего вещества.

Внешние – потери, возникающие за пределами тех мест, где течет рабочий пар (газ).

Внутренние потери

1. Основные потери в проточной части: в соплах, на рабочих лопатках, с выходной скоростью,

2. Вследствие наличия связной проволоки,

3. Вследствие парциального впуска,

4. На трение дисков и бандажной ленты и на вентиляцию рабочих лопаток,

5. 0т влажности пара, (для паровых турбин),

6. 0т утечек через наружные и внутренние уплотнения,

7. В зазорах облопатывания,

8. В перепускных трубах (ресиверах) между корпусами турбоагрегата и на выпускную скорость в конденсатор (для паровых турбин),

9. Потери тепла в окружающую среду.

Все внутренние потери учитываются "внутренним относительным КПД" отдельной ступени или же всей турбины в целом _oi.

; ;

Внешние потери

1. 0т трения в подшипниках турбоагрегата,

2. В передаче между турбиной и электрогенератором (если таковая имеется),

З. В электрогенераторе при трансформации энергии.

Рассмотрим каждую из перечисленных внутренних потерь.

1. Факторы и зависимости, определяющие потери в соплах h_c, на рабочих лопатках h_л и с выходной скоростью h_вс были подробно рассмотрении ранее.

2. Потери вследствие наличия связной проволоки.

Наличие связной проволоки ухудшает условия течения потока, создает препятствие на пути его движения, зоны завихрения, что приводит к увеличению коэффициента профильных потерь _пр и снижению КПД ступени.

В зависимости от высоты рабочих лопаток, места расположения, количества рядов и диаметра проволоки снижение КПД может достигать от 3,6 до 11 %.

Для учета влияния связной проволоки предлагаются различные методы.

Один из них, позволяющий оценивать увеличение коэффициента профильных потерь _пр показан на рис. 51.

3. Потеря вследствие парциального впуска

При парциальном впуске пара (если  < 1) межлопаточные каналы на рабочей решетке заполнены рабочим паром только в той части рабочего колеса, которая в данный момент находится против сопел. Все остальные межлопаточные каналы заполнены стоячим паром. При подходе этих каналов к соплам рабочий пар должен вытолкнуть из каналов стоячий пар. На это выталкивание (выколачивание) расходуется часть располагаемой энергии. Возникающая при этом потеря энергии иногда именуется "потерей на выколачивание" и может быть определена из выражения

Для одновенечной ступени коэффициент потери энергии на выколачивание может быть найден из выражения:

где В₂ – м – ширина рабочей решетки,

m – число групп сопел, если они находятся достаточно далеко друг от друга,

c₀ – м/с – условная скорость истечения м/с,

 – степень парциальности одного сегмента сопел.

Если  =1, то формула теряет смысл, а h_п = 0.

Для двухвенечной ступени один из частных вариантов формулы:

; ; D_ср – м

4. Потери энергии на трение дисков и бандажной ленты и на вентиляцию рабочих лопаток

При вращении ротор соприкасается с паровой (газовой) средой, в результате чего имеет место трение среды о вращающиеся поверхности ротора; на преодоление возникающих сил трения затрачивается некоторая мощность, трансформирующаяся в тепловую энергию.

В турбинах с ротором дискового типа трение о среду возникает на боковых поверхностях дисков, а в роторах барабанного типа на торцевых стенках барабанов (рис. 52).

В потере на трение диска и бандажа, если бандаж приклепан к рабочим лопаткам при помощи шипов с головками, около 40 % теряемой мощности приходится на район бандажа, т.к. он находится в зоне наибольшей скорости.

Потеря на. вентиляцию рабочих лопаток возникает при  < 1 на участке холостого пробега. Застойный пар в межлопаточных каналах под действием центробежной силы начинает циркулировать (рис. 53а).

Кроме того, на том же, участке возникает трение о застойный пар сильно ребристых участков входной и выходной кромок рабочей решетки (рис. 53б).

Проводившиеся исследования показали, что потери энергии на трение и вентиляцию возрастают при увеличении

1. плотности среды, в которой вращается диск,

2. среднего диаметра ступени,

3. длины рабочих лопаток,

4. окружной скорости ступени

и при уменьшении степени парциальности впуска .

Потери на вентиляцию уменьшаются с уменьшением зазора между корпусом турбины и рядом рабочих лопаток. Для уменьшения этого зазора вдоль нерабочей части колеса делаются прикрывающие щитки (рис. 53в), позволяющие уменьшить мощность, теряемую на вентиляцию в 2  3 раза.

Для определения мощности, теряемой на трение и вентиляцию, предложено довольно много различных формул. Наиболее универсальная из -них – эмпирическая формула Стодола, учитывающая сразу потери на трение диска и на вентиляцию рабочих лопаток:

для одно венечной ступени

кВт

для перегретого пара  = 1; для влажного  = 1,2  1,3

 – полная степень парциальности впуска,

_к – относительная длина дуги окружности, прикрытая щитками.

D_ср – м; – см; u – м/сек;

V – м³/кг – средний удельный объем пара в районе диска

Для двухвенечной ступени вместо величины подставляется сумма .

Некоторые авторы предлагают рассчитывать отдельно мощности, теряемые на трение дисков N_тр и на вентиляцию рабочих лопаток N_в. Так, например, на основании опытов НЗЛ получены следующие формулы:

мощность, теряемая на трение диска

кВт

 = 8,5  17 – коэффициент, зависящий от расстояния между диском и стенками камеры (т.е., соседними диафрагмами); меньшее значение – при небольших расстояниях, большее – при больших.

D_ср – м; u – м/сек; g = 9,81 м/сек; кг/м³

мощность, теряемая на вентиляцию для одновенечной ступени:

кВт

где –м; D_{ср –} м; и т.д.

коэффициент 480 – при наличии прикрывающих щитков,

900 – при их отсутствии.

Формула справедлива при = 17  50 мм.

Для двухвенечной ступени

кВт

D_ср, и – м;

При наличии прикрывающих щитков потеря уменьшается вдвое.

Мощность, теряемая на трение и вентиляцию, переходит в тепло, которое воспринимается потоком пара.

Соответственно кДж/кг

Потеря на трение и вентиляцию имеет существенное значение в малых турбинах (при небольших расходах пара G), а так же на первых ступенях турбоагрегатов с высоким начальным давлением пара. В ступенях мощных паротурбинных агрегатов эта потеря, как правило» мала. Особенно это относится к последним ступеням.

5. Потери от влажности пара

Влажный пар – двухфазная среда. При существующей на сопловом аппарате разности давлений Р₀ – Р₁ капельки воды на выходе из сопловых каналов имеют абсолютную скорость c_1в меньшую, чем скорость пара с₁ при сохранении одного и того же направления векторов. В результате, при какой-то единой окружной скорости u относительные скорости входа парового потока на рабочую решетку W₁ и капелек воды W_1в будут отличаться по величине и направлению (рис. 54). Возникает удар капелек воды в спинку рабочих лопаток с соответствующей потерей кинетической энергии.

Существуют различные методы оценки снижения КПД турбинной ступени, работающей во влажном паре.

Один из них заключается в следующем. В тепловой диаграмме (рис. 55) строится процесс расширения пара по “сухому пару”, т.е., с учетом всех потерь, но без учета потери от влажности; при этом определяется внутренний теплоперепад по "сухому пару":

и откладывается на диаграмме. В точке 2 снимается величина паросодержания Х₂ и после этого оценивается КПД ступени с учетом влажности.

6. Потери от утечек через наружные и внутренние уплотнения

Как наружные, так и внутренние уплотнения паровых и газовых турбин выполняются в большинстве случаев лабиринтового типа.

Принцип действия: пар (газ) проходит через ряд узких щелей (лабиринтов), за каждой из которых следует относительно широкая камера.

Весь перепад давлений, приходящийся на рассматриваемое уплотнение, распределяется между лабиринтовыми камерами, расположенными последовательно одна за другой: 1, 2, 3 и т.д. (рис. 56а).

П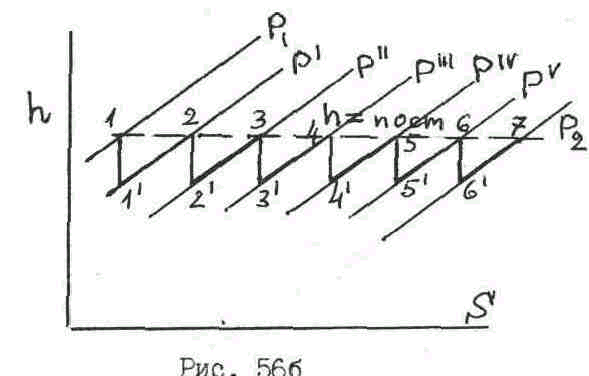ри проходе через первую щель давление пара снижается от Р. до Р'.

Возникающая при этом расширении скорость, благодаря удару о стенку камеры, полностью теряется и вследствие этого энтальпия в камере 1 вновь повышается до исходного значения перед первой щелью.

Во второй камере давление падает до Р’’, а скоростная энергия вновь полностью превращается в тепловую, повышая энтальпию к камере до исходного значения h₁ и т.д. Данный процесс представлен на рис. 56б. Здесь 1 – 1'; 2 – 2'; 3 – 3’ и т.д. – процессы изоэнтропийного расширения в щелях. 1’ – 2; 2' – 3 и т.д. – повышение энтальпии в камерах за счет потери скорости потока.

Таким образом, общий процесс расширения в уплотнении происходит по линии дросселирования, т.е., по линии h₁ = пост.

Исходя именно из этих представлений были получены все расчетные формулы, которые даются ниже.

Величина утечек через наружные уплотнения может быть учтена только количественным способом.

Влияние утечек через внутренние уплотнения может быть учтено двумя способами: количественным и качественным.

Утечка через наружные уплотнения

Расход пара (газа) через ножевое лабиринтовое уплотнение с проточками по валу (рис. 56а) может быть найден из выражения:

кг/сек

где _у – коэффициент расхода, учитывающий, что площадь поперечного сечения потока меньше, чем площадь щели, т, к, ’ <  (рис. 57)

_у – функция формы гребня, его толщины у зазора  и величины зазора .

Практически   0,3  0,5 мм

  0,2  0,6 мм

а величина _у лежит в пределах

_у = 0,95  0,7

м²

где d – м – диаметр вала под уплотняющими гребнями;

 – м – зазор в уплотнении.

Р₀ – кг/м² – давление перед уплотнением,

V₀ – м³/кг – удельный объем перед уплотнением; ,

где Р₁ – давление за уплотнением; z – число гребней.

Утечка через уплотнения диафрагм (внутренние уплотнения) может быть найдена из выражения

кг/сек

где _{кр –} критическое отношение давлений. Остальные величины – в той же размерности, что и в предыдущей формуле.

Схема потоков пера при количественное способе учета утечек дана на рис. 58. Протечки пара внутри корпуса – через уплотнения диафрагм и через разгрузочные отверстия в дисках.

Врасчетную формулу для определения мощности каждой ступени входит количество пара, фактически проходящее через её сопла, т.е.

и т.д.

Качественный способ учета утечек в уплотнениях диафрагм

Он основан на том, что пар, проходящий через внутренние уплотнения, остается при постоянной энтальпии, равной h₀. Смешиваясь затем с основным потоком этот пар повышает энтальпию последнего, т.е., получается недоиспользование тепловой энергии.

Соответствующая потеря

где (один из возможных вариантов расчетной формулы/.

Обозначения величин – те же, что и в предыдущих формулах.

7. Потери в зазорах облопатывания

а). Потери через радиальные зазоры облопатывания

Потери в радиальных зазорах пропорциональны разности давлений на лопаточном венце, величине зазора и становятся ощутимыми при степени реакции > 0,2.

Схема протечек в ступени реактивной турбины показана на рис. 59.

Физический смысл потери состоит в том, что пар (газ), проходящий через щель, дросселируется, сохраняя свою энтальпию, т.е., часть энергии потока недоиспользуется.

;

где a = 3  4,5 при  =0,25  0,5.

Формула учитывает общую потерю от утечки через зазоры сопловой решетки и рабочей решетки.

Если принят вариант турбинных ступеней со степенью реакции более 0,2 при дисковой конструкции ротора и размещении сопловых аппаратов в диафрагмах, то здесь также может иметь место протечка рабочего тела в обход рабочих лопаток. Для уменьшения протечки при  > 0,2 принимаются конструктивные меры – делаются радиальные и осевые уплотнения (рис. 60). При  <:0,2 имеет место компенсация тенденции к протечке подсасывающим действием струи.

б). Осевые зазоры облопатывания

Наибольшее влияние на поток оказывают осевые зазоры между сопловой и рабочей решетками турбинной ступени. Струя, вышедшая из сопловых каналов, взаимодействует здесь с окружающий средой там, где имеется контакт. Возникает подсос из окружающей среды, в результате чего снижается скорость с₁. Таким образом, для уменьшения подсоса надо по возможности снижать величину осевого зазора.

Однако, с другой стороны требуется увеличение осевого зазора, т.к. в нем происходит выравнивание неравномерности поля скоростей потока, выходящего из сопловых каналов. Это способствует повышению КПД ступени, но до определенных значений величины зазора, а далее КПД начинает падать. Таким образом, существует оптимальное значение осевого зазора.

При всем этом осевые зазоры должны быть такими, чтобы обеспечить безусловную надежность работы облопатывания, исключить касание рабочих лопаток о сопловой аппарат при всех возможных смещениях ротора и его элементов (температурные расширения, колебания лопаток, износ элементов упорного подшипника и т.д.).

Конструктивно осевые зазоры могут быть разделены на закрытые () и открытые (’).

Назначение закрытого зазора заключается в выравнивании неравномерности потока. Он не должен быть очень малым, т.к. не выполнит своего основного назначения. При очень большом зазоре – увеличение осевых размеров ступени и турбины.

Надежность эксплуатации обеспечивается величиной открытой части зазора.

На основании исследований и по данным практики оптимальные значения зазоров составляют

 = 3,5  6,0 мм; ’ = 1,0  2,5 мм

Если осевые зазоры назначены в этих пределах, то потери на подсос рабочего тела через зазор ’ учтены значениями коэффициентов _л и .

Неблагоприятное влияние осевых зазоров имеет место преимущественно у активных ступеней. У реактивных ступеней засасывание рабочего тела через осевой зазор отсутствует.

Построение процесса турбинной ступени в диаграмме h-sс учетом всех рассмотренных потерь.

В реактивной ступени потеря от парциальности впуска отсутствует, т.к. всегда  = 1.

При барабанной конструкции ротора в промежуточных ступенях потеря на трение и вентиляцию также отсутствует.

Внутренний относительный КПД

для одной ступени

для турбины в целом

8. Потери в перепускных трубах между корпусами турбоагрегата и на выпускную скорость в конденсатор

Данные потери могут быть оценены, если принять скорость течения пара в ресиверах и в выхлопном патрубке турбины. Соответственно

для ресиверов c_p = 50  80 м/с

для выхлопных патрубков c_па = 70  120 м/c

При построении процесса течение пара в ресивере принимается изоэнтальпийным (рис. 63).

Здесь Р’_р – давление за ресивером,

Р_z – давление за последней ступенью турбины,

Р_к – давление в конденсаторе.

Потери в ресиверах – численно незначительная величина – меньше 0,5 % от общего располагаемого теплоперепада в турбине.

9. Потери тепла в окружающую среду

Причина потерь – разность температур. Постановка изоляции уменьшает потери и позволяет создать нормальные условия работы персонала.

Кроме того, за счет изоляции создается равномерное температурное поле в металле самого корпуса, не допускающее его коробления и перекосов и, соответственно, осложнений при эксплуатации турбины.

Величина потерь тепла очень мала – меньше 0,5 % от его общего количества, поэтому в тепловых расчетах не учитывается.

Внешние потери

Потери от трения в подшипниках турбоагрегата, в передаче между турбиной и электрогенератором (для турбин очень маленькой мощности) и в электрогенераторе при трансформации энергии зависят главным образом от мощности установки. Соответствующий характер зависимости КПД от мощности представлен на рис. 64.

Величины КПД (ориентировочно):

механический КПД (потери в подшипниках)

_м = 0,97  0,996

КПД зубчатой передачи

_р = 0,96  0,975

КПД электрогенератора (зависит, кроме того, от способа охлаждения: воздушное или водородное)

_эг = 0,925  0,988

Общий оценочный КПД турбоагрегата и установки в целом

Общий КПД определяется как произведение КПД, оценивающих эффективность отдельных участков процесса преобразования энергии.

Термический КПД (абсолютный КПД идеального цикла) – в общем случае:

; h_к – энтальпия конденсата.

Относительный внутренний КПД

Абсолютный внутренний КПД

Механический КПД

Относительный эффективный КПД

Абсолютный эффективный КПД

КПД электрогенератора

Относительный электрический КПД

Абсолютный электрический КПД

КПД паросиловой установки в целом

Где – КПД парогенератора,

–коэффициент, учитывающий потерю тепла через изоляцию паропроводов,

–учитывает расход энергии на собственные нужды.

Наивысшие значения КПД, достигнутые в опытно-промышленных установках при наличии промперегрева пара и развитой регенеративной системе подогрева питательной воды:

Япония N_э = 700 МВт, P₀ = 31 МПа, t₀ = 566 С, = 48,4%, = 41,9%

США N_э = 500 МВт, P₀ = 35 МПа, t₀ = 650 С, = 49%, = 42,5 %

Расход рабочего вещества и тепла на турбину и мощность, развиваемая турбиной

Располагаемый теплоперепад Н₀ кДж/кг, КПД турбины , часовой расход рабочего вещества D кг/ч и развиваемая мощность N_э кВт (при отсутствии отборов пара), связываются между собой следующей логической зависимостью

откуда кг/ч

Удельный расход пара кг/кВтч

В конденсационных турбинах эта величина, ориентировочно, лежит в пределах 3,1  4,5 кг/кВтч

Удельный расход тепла (при отсутствии регенеративного подогрева питательной воды):

кДж/кВтч

Выражение для определения мощности, развиваемой турбиной, может быть получено следующим образом

, где G – кг/с – расход рабочего тела.

Отсюда кВт

Данная зависимость будет справедлива для отдельно взятой ступени

кВт

и для отсека турбины

Мощность, развиваемая турбиной при наличии отборов пара

Примем следующие обозначения:

G - кг/с – расход пара на турбину;

G_отб1, G_отб2 – кг/с – расход пара в отборы;

Р₁ и Р₂ - давление отбираемого пара, МПа;

h_0I; h_0II; h_0III – кДж/кг – располагаемые теплоперепады по отсекам;

G_I; G_II; G_III – расход пара по отсекам, кг/с. G_I = G

Мощность, развиваемая турбиной, складывается из суммы мощностей каждого отсека, т.е.

Работа паровых турбин при переменных режимах

Переменными называются режимы работы турбоагрега­та, при которых мощность или параметры пара отличаются от номинальных. Соответственно, различают две группы переменных режимов:

1. режимы обеспечения требующейся мощности при номинальных параметрах пара,

2. режимы с изменением начальных параметров пара – давления и температуры – и давления в конденсаторе.

Переменные режимы являются обычными эксплуатационными режимами, особенно первой группы, т.к. требующаяся мощность меняется и, в соответствии с этим, нагрузка на турбоагрегат.

Переменные режимы для обеспечения требующейся мощности

Обеспечение требующейся мощности (регулирование мощности) в паровых турбинах может быть:

1. количественное – изменением расхода пара

сюда относится: а). сопловое регулирование,

б). обводное регулирование,

в). отключением верхних регенеративных отборов пара.

2. качественное регулирование – изменением параметров пара, поступающего непосредственно в проточную часть турбины - дроссельное регулирование.

При сопловом регулировании перед первой ступенью турбины размещается сопловая коробка (рис. 66) с несколькими сопловыми клапанами, открывающимися в определенной последовательности и обеспечивающими нужный пропуск пара.

При обводном регулировании при полном открытии сопловых клапанов и достижении их максимальной пропускной способности открывается обводной клапан (рис. 67), через который подводится дополнительное количество пара, что обеспечивает нужное увеличение мощности.

Одним из наиболее эффективных способов покрытия пиковых нагрузок и создания аварийного и ремонтного резервов в энергосистемах является, как показали исследования в СССР и за рубежом, использование дополнительной мощности, которая может быть получена на конденсационных блоках за счет временного отключения верхних регенеративных отборов турбины (рис. 68) при сохранении постоянным расчетного расхода свежего пара.

Отключение одного отбора дает увеличение мощности порядка 3,5 %, двух – совместно до 8 %. Экономичность работы турбоагрегата при этом, естественно, падает, но при указанных выше обстоятельствах это является вполне приемлемым.

При дроссельном регулировании за стопорным клапаном по ходу пара располагается дроссельный клапан (рис. 69), который при постоянном давлении пара перед турбиной регулирует, в зависимости от требующейся мощности, давление пара непосредственно перед проточной частью, а также и количество поступающего пара.

Влияние различных способов регулирования мощности на тепловой процесс в турбине

Тепловой процесс в турбине на переменных режимах существенно отличается от теплового процесса на расчетном режиме.

В турбину, имеющую вполне определенную проточную часть, размеры которой определены из расчета на основном режиме, попадает на уменьшенных мощностях соответственно меньшее количество рабочего вещества или же при измененных параметрах. Так как проточная часть турбины не может меняться (за исключением первой ступени при наличии соплового регулирования), то, естественно, произойдет перераспределение теплоперепадов между ступенями и тепловой процесс в турбине изменится по сравнению с режимом номинальной нагрузки.

Хотя при изменении режима работы турбины одновременно может меняться несколько параметров, рассмотрим сначала влияние на тепловой процесс турбины отдельных параметров.

Количественное регулирование – изменением расхода пара.

Рассмотрим первоначально особенности работы последней ступени турбины.

Условие неразрывности струи сохраняет свою силу независимо от изменений расхода рабочего вещества в турбине

Если при изменении режима работы турбины расход пара изменится и станет равным G’, то для последней ступени , где G’, V’, c₁’ – величины, соответствующие измененному режиму работы.

Проточная площадь последней ступени f является величиной постоянной.

Давление за турбиной (пара в конденсаторе) с изменением нагрузки немного меняется, но это изменение незначительно и в данном случае им можно пренебречь. Поэтому можно считать \/'  \/

Взяв отношение второго уравнения неразрывности к первому имеем , т.е., если расход пара в турбине уменьшается, то во столько же раз уменьшается скорость пара c₁'; с увеличением расхода пара происходит увеличение c₁’.

Скорость истечения c₁ прямо пропорциональна корню квадратному из располагаемого теплоперепада (для активного типа турбинной ступени). Поэтому с изменением расхода пара в турбине располагаемый теплоперепад в последней ступени изменяется в том же направлении, как и расход пара.

При сопловом регулировании расход пара через первую ступень может изменяться за счет изменения количества работающих групп сопел (изменения проточной площади). Но за ступенью при всех режимах паровое пространство остается неизменным V_р = пост.

В свою очередь где G;G’ – расходы пара на соответствующих режимах, а V_р и V’_р – удельные объемы пара за первой (регулировочной) ступенью на тех же режимах.

Таким образом, получается, что с уменьшением расхода пара G’ удельный объем его за ступенью V'_р должен увеличиваться.

Увеличение же объема связано с уменьшением давления Р'_р в этом же месте; отсюда – при уменьшении расхода пара G’, давление за регулировочной ступенью Р’_р также будет уменьшаться.

При неизменных начальных параметрах пара Р₀ и t₀ это приводит к увеличению располагаемого теплоперепада h’_op на регулировочной ступени.

При увеличении расхода пара G'' удельный объем V''_р уменьшается, давление за ступенью Р''_р растет и располагаемый теплоперепад h''_op становится меньше.

В результате, наибольшее изменение теплоперепадов происходит в двух ступенях: первой и последней. Изменение теплоперепадов во всех промежуточных ступенях не носит столь резко выраженного характера. Суммарная величина теплоперепадов от второй до предпоследней ступени включительно при изменении расхода, пара является практически постоянной. Характер изменения теплоперепадов показан на рис. 70.

Качественное регулирование – дросселированием пара.

При данном способе регулирования проточные площади всех ступеней в турбине остаются неизменными, а изменение режима работы достигается дросселированием пара при впуске в турбину.

Дроссельный клапан является при этом как бы первой ступенью, срабатывающей перепад давления с Р₀ до Р’₀ и имеющей нулевой КПД; действительная первая ступень турбины при таком способе регулирования работает примерно в тех же условиях, как вторая ступень при количественном регулировании.

При регулировании с помощью дроссельного клапана изменение параметров пара неизбежно связано с изменением его расхода: с прикрытием клапана расход пара уменьшается. При дросселировании пара общий располагаемый теплоперепад в турбине уменьшается; в то же время уменьшается располагаемый теплоперепад в последней ступени вследствие уменьшения расхода пара в турбине. Общее уменьшение теплоперепада примерно равно уменьшению теплоперепада в последней ступени; при этом теплоперепады в остальных ступенях меняются сравнительно мало. Таким образом, в турбине с дроссельным регулированием при изменении расхода пара теплоперепад сильно меняется только в последней ступени. Тепловой процесс показан на рис.71.

Из изложенного выше следует, что при всех способах регулирования мощности основным фактором, влияющим на характер теплового процесса и режим работы турбины, является расход пара.

Зависимость расходов рабочего вещества и давлений в ступенях при переменных режимах в многоступенчатых турбинах

Изменение расхода рабочего вещества в турбине неизбежно связано с перераспределением теплоперепадов, а следовательно, начальных и конечных давлений этого вещества в каждой ступени.

В турбинах с сопловым регулированием начальное давление пара перед первой ступенью практически не зависит от расхода рабочего вещества.

Поэтому все дальнейшие положения по определению параметров рабочего вещества будут справедливы для всех ступеней , начиная со второй, при чисто количественном регулировании, и начиная с первой – при дроссельном регулировании. В последнем случае роль регулирующей ступени выполняет, как указывалось выше, сам дроссельный клапан.

Для турбин, работающих во всех ступенях с докритическими скоростями, Флюгелем аналитически была выведена формула, связывающая расход и параметры рабочего вещества

где G – расход рабочего вещества при параметрах Р₀; Т₀; Р₂

G’ - то же, при Р’₀; Т’₀; Р’₂. Здесь Т₀ – температура рабочего вещества в градусах абсолютной шкалы.

Когда Р₂ мало по сравнению с Р₀, то можно пренебречь величинами и . Тогда получаем

Поскольку температура в данном случае принимается в градусах абсолютной шкалы, то её изменение при переменных режимах в реальных условиях (10  15 °С) малозаметно и можно считать Т₀  Т’₀.

В результате имеем .

Данные формулы приложимы и к одной ступени турбины, и к группе ступеней при условии, что проходные сечения рассматриваемых ступеней не меняются.

Хотя исходная формула выведена при ряде допущений, она, как и её производные, хорошо подтверждаются опытными данными и могут служить основными зависимостями при расчетах.

Изменение степени реакции в ступени

При переменных режимах величина степени реактивности в ступенях турбины меняется при всяком отклонении располагаемого теплоперепада от его значения на расчетном режиме. С изменением теплоперепада изменяется скорость с₁, а значит их характеристика

С увеличением X₁ реактивность возрастает; при уменьшении X₁ может появиться даже отрицательная реакция.

Профессор И.И. Кириллов аналитически вывел зависимость между степенью реакции и величиной X₁ при различных значениях начальной степени реакции на расчетном (основном) режиме. Данная зависимость (рис. 72) была подтверждена и экспериментальными исследованиями.

Кривые показывают, что при больших исходных значениях степени реакции ₀ и изменении при этом X₁ реактивность меняется незначительно. Лишь в активных ступенях отклонение X₁ от расчетной величины вызывает существенную реактивность – положительную или отрицательную.

Изменение КПД при переменных режимах

При переменных режимах имеет место изменение КПД отдельных ступеней (в первую очередь первой и последней) и, как следствие, всего паротурбинного агрегата в целом.

Причины: 1. на первой и последней ступенях изменяется располагаемый теплоперепад, а значит и с₁. При постоянной окружной скорости u изменяется направление вектора относительной скорости W₁ и угол ₁. Как следствие – возникает удар потока о входную .кромку рабочей решетки.

2. с изменением располагаемого теплоперепада и скорости c₁ изменяется и характеристика ступени X₁, отклоняясь от наивыгоднейшего значения; в результате – падение КПД.

3. изменяется степень реакции ступени, отклоняясь от расчетной.

Все указанные причины ведут к снижению КПД турбины в целом. При дроссельном регулировании, кроме того, падение общего КПД имеет место за счет потери при мятии пара в дроссельном клапане.

Внутренний относительный КПД при дроссельном регулировании

где Н₀ - располагаемый теплоперепад турбины при начальных параметрах пара до дросселирования,

H₀ – то же, при начальном давлении после дросселирования (непосредственно перед соплами первой ступени),

_oi – внутренний относительный КПД проточной части,

_д – коэффициент дросселирования.

Переменные режимы паротурбинного агрегата при изменении параметров пара

При эксплуатации паротурбинного агрегата может иметь место отклонение начальных и конечных параметров пара от их расчетных значений. Причины:

1. изменение Р₀ и t₀ возможно из-за нарушения режима работы котельной установки или же сознательного снижения начальной температуры пара t₀.

Значительное отклонение является ненормальным.

2. изменение давления в конденсаторе зависит от температуры охлаждающей воды. Оно связано с сезонными изменениями температуры и является неизбежным.

При проточном водоснабжении давление в конденсаторе может изменяться от 0,02 кгс/см² зимой до 0,08 кгс/см² летом. Всякое изменение начальных и конечных параметров влияет на характер протекания процесса расширения пара в турбине, а следовательно и на мощность, ею развиваемую. Рассмотрим влияние каждого из трех основных параметров: Р₀, t₀ и Р_к.

Влияние изменения начального давления.

Принимаем Р₀ = переменное

t₀ = пост. и Р_к = пост.

Если Р’₀ < Р₀, то Н’₀ < Н₀ (Рис. 74)

и внутренняя мощность турбины

Влияние изменения начальной температуры

Принимаем t₀ = переменна

Р₀ = пост. и Р_к = пост.

Если t’₀ < t₀ то Н’₀ < Н₀ (Рис. 75)

и внутренняя мощность турбины

Снижение начальной температуры на 20  25 С дает уменьшение мощности примерно на 1 %

Влияние изменения давления пара в конденсаторе

Принимаем Р_к – переменно

Р₀ = пост. и t₀ = пост.

Если Р’_к > Р₀, то Н’₀ < Н₀ (Рис. 76)

Если Р’’_к < Р_к, то Н’’₀ > Н₀

Во всех случаях на мощность, развиваемую турбиной, влияет изменение КПД_oi из-за изменения влажности пара на последних ступенях.

Конструктивные особенности выполнения последней ступени мощных конденсационных турбин

Конструктивное выполнение последней ступени конденсационной турбины представляет большой интерес, т.к. размеры проходных сечений этой ступени определяют максимальную мощность, на которую может быть построена турбина.

Как известно кВт.

Расход пара G - ограничивается пропускной способностью последней ступени (здесь наибольший объем пара).

Пропускная способность зависит от проточной площади последней ступени и удельного объема пара в ней.

В свою очередь

Величины D_срz и ограничиваются условиями прочности рабочих .лопаток последней ступени из-за возникающей здесь большой центробежной силы. При работе турбины с 3000 об/мин и стальных рабочих лопатках предельные допустимые значения составляютD_срz  2,5 м и 1,0 м.

В результате, для однопроточной турбины с учетом уменьшения расхода пара на последней ступени за счет отборов максимальная возможная мощность составляет порядка 100 МВт.

Пути увеличения пропуска пара через последнюю ступень (а значит и увеличения единичной мощности турбоагрегатов):

1. разветвленный выхлоп пара в конденсатор;

Турбина выполняется двухкорпусной: с корпусами высокого и низкого давления. Корпус низкого давления делается двухпроточным (рис. 77). Рабочие лопатки последней ступени каждого протока выполнены с предельной пропускной способностью, т.е., пропуск пара и мощность турбоагрегата могут быть увеличены примерно вдвое.

Могут быть приняты два двухпроточных корпуса НД; возможный пропуск пара и мощность возрастают, соответственно, в четыре раза и т.д.

2. полуторный выхлоп пара (ступень Баумана);

В этом случае принимаются рабочие лопатки предельной длины для предпоследней и последней ступеней, а после предпоследней ступени часть пара в обход последней ступени сбрасывается в конденсатор (рис. 78). Полуторный выхлоп может сочетаться с двойным потоком как например у турбин К-210-130.

3. двухвальные турбоагрегаты;

Турбоагрегат выполняется двухвальным (рис. 79) с пониженным числом оборотов ротора корпуса низкого давления (в практике США – в части высокого давления 3600 об/мин, низкого давления – 1800 об/мин).

Понижение числа оборотов позволяет при предельно допустимой величине центробежной силы в рабочих лопатках последней ступени увеличить их длину и средний диаметр, а значит и пропускную способность. Данный вариант применяется совместно с разветвленным выхлопом.

4. применение легких металлов;

Применение легких металлов для изготовления рабочих лопаток последней ступени позволяет при допустимой величине центробежной силы увеличить длину лопаток. Предпочтение отдается сплавам на базе титана (плотность титана 4,5 против 7,85 для стали). Подобный вариант был принят для изготовления рабочих лопаток длиной 1200 мм отечественной турбины мощностью 1200 МВт.

5. увеличение угла ₂ на последней ступени;

Увеличение угла ₂ дает увеличение выходного сечения рабочей решетки и её пропускной способности.

В части высокого и среднего давления турбины угол ₂ обычно лежит в пределах 15  19 градусов, а на последней ступени он принимается до 32  33 градусов.

6.увеличение степени реакции на последней ступени;

В современных турбоагрегатах степень реакции в ступенях высокого и среднего давления обычно лежит в пределах 0,15  0,25, а на последней ступени доходит до 0,54  0,614. Это дает увеличение скорости W_2z и, при имеющейся проходной площади – увеличение пропускной способности.

7. повышение давления в конденсаторе;

Повышение давления на выхлопе из турбины дает уменьшение удельного объема пара и при имеющейся проточной площади – возможность увеличения массового расхода.

Обычно давление в конденсаторе находится на уровне 0,035 кгс/см², а в зарубежной практике в ряде случаев для мощных паротурбинных агрегатов эта величина составляет 0,07  0,105 кгс/см².

Это, естественно, дает снижение термического КПД и понижение общего КПД турбоагрегата, но при определенных условиях в целом оказывается выгодным.