1.3. Коэффициент полезного действия и удельная работа действительного цикла гту

Действительный цикл газотурбинной установки отличается от теоретического прежде всего наличием внутренних необратимых потерь, которые являются следствием наличия гидравлических сопротивлений по трактам ГТУ, несовершенством преобразования энергии в осевых компрессорах и газовых турбинах, механических потерь в подшипниках, неполноты сгорания топлива, потерь тепла в окружающую среду со стороны внешнего корпуса установки, а также утечек рабочего тела через различные лабиринтные уплотнения. В реальных установках, эксплуатируемых на газопроводах, неизбежны также вспомогательные расходы энергии: на привод топливных и масляных насосов, подогрев топлива, на вентиляторы воздушного и масляного охлаждения и т. д.

В силу этого приведенный эффективный КПД газотурбинной установки можно представить как произведение следующих сомножителей:

(1.16)

где - КПД эффективно-термодинамического цикла ГТУ;- КПД систем организации цикла ГТУ;- коэффициент, учитывающий утечки рабочего тела в цикле установки.

Эффективно-термодинамическим циклом газотурбинных двигателей называются круговые процессы, удовлетворяющие требованиям термодинамической теории тепловых двигателей и требующего наименьшего количества эмпирических данных для расчетного определения основных показателей внутренних процессов реальных двигателей – коэффициента полезного действия и удельной работы ГТУ [3].

Естественно, что основным сомножителем в выражении (1.16) является величина , определяемая видом цикла, термодинамическими и гидродинамическими характеристиками действительных процессов в установке.

На Рис. 1.7 приведены принципиальная схема простейшей одновальной ГТУ (в целях простоты рассмотрения) и ее действительный цикл в координатах p-vиT-sсо сгоранием топлива в процессеp=idem. Следует отметить, что в показателях одновальной и двухвальной установки на номинальном режиме работы нет принципиальной разницы.

Определим для этой установки выражение эффективно-термодинамического КПД - _с. С учетом соотношений (1.2) и (1.3) потенциальные работы расширения в турбине W_T и сжатия в компрессоре W_K имеют вид (цифрами со штрихом отмечены фактические параметры рабочего тела на выходе компрессора и газовой турбины):

(1.17)

W_K = (1.18)

где _к и _т - соответственно внутренние относительные КПД компрессора и газовой турбины.

Введем в расчеты коэффициенты, отражающие необратимость действительных процессов цикла:

Изменение физических свойств воздуха в процессе сжигания в нем топливного газа

(1.19)

гидродинамические потери в трактах газотурбинной установки

(1.20)

Введение этих коэффициентов позволяет преобразовать выражение (1.17) - работы расширения к виду () :

(1.21)

Полное количество тепла, подведенного к воздуху в камере сгорания

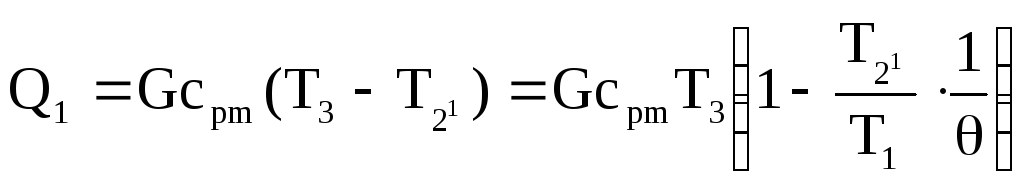(1.22)

Соответственно будет формироваться расчетное выражение эффективно-термодинамического КПД цикла ГТУ [2]:

(1.23)

где

(1.24)

(1.25)

_m – приведенный эффективный КПД турбомашин:

(1.26)

В отличие от теоретического цикла, функция (1.23) при заданных значениях температурной характеристики , КПД турбомашин и гидравлических сопротивлений имеет максимум по параметру , или, что то же, по величине _k.

Очевидно, что характер зависимостей _с = _с () определяется характером двух кривых -  = 1 - =  () и (). На диаграммах Рис. 1.8 приведены все эти три функции при  = 4: для теоретического цикла а), цикла с учетом только относительных значений КПД турбомашин б),(_к = _т = 0,85) и цикла, учитывающего гидравлические сопротивления в),(_к = _т = 0,85; ₁ = 1; ₂ = 0,9).

Данные диаграмм Рис. 1.8 показывают, что во всех случаях величины коэффициентов полезной работы  = 1-  и относительной характеристики подвода тепла с повышением значения монотонно снижаются вплоть до нулевого значения. Изменение _с определяет различный характер протекания этих зависимостей. В теоретическом цикле условия  = 0 и = 0 имеют место при одном и том же значении = . Введение в расчеты потерь в турбомашинах (их относительных КПД ) приводит к тому, что повышается крутизна прямой линии  =  (₎ и, что главное, численное значение  = 0 получается при меньших значениях , нежели = 0. Именно это обстоятельство и приводит к образованию максимума функции_с и прохождению ее через вторую нулевую точку. Гидравлические сопротивления еще в большей степени усугубляют это положение – сдвиг функции _с = _с () в сторону меньших значений величины  приводит и к снижению численного значения самой этой функции в).

Влияние гидравлических сопротивлений на КПД установки зависит от величины коэффициента полезной работы  = 1 - . Чем выше этот коэффициент , тем меньше чувствительность цикла к необратимым потерям. Если принять, например,  = 0,6-0,7, то оказывается, что снижение коэффициента ₂ на 1% приводит к повышению КПД цикла на 2,5-3%, что весьма ощутимо.

Следует отметить, что на положение экстремума самой кривой _с = _с (_k) влияет вид закона сопротивлений по трактам ГТУ, который принимается в расчетах установки в качестве независимой величины. Наиболее часто в расчетах используется закон о неизменности абсолютной величины потерь напора в отдельных элементах установки (на входе осевого компрессора, по камере сгорания ГТУ, на выхлопе газовой турбины и т.д.).

Численная величина потери мощности ГТУ при известном сопротивлении какого-либо участка установки может быть определена по следующему соотношению, непосредственно вытекающего из понятия потенциальной работы сжатия (расширения):

1. для воздушной стороны ГТУ (участок, вход воздуха – камера сгорания)

N_в = p_вV_в^-1_к 10^-3 , кВт

2. для газовой стороны НТУ (выход турбины – дымовая труба)

N_г. = p_гV_г_т 10^-3 , кВт

где р_в , р_г - соответственно гидравлические сопротивления рассматриваемых участков воздушного и газового трактов ГТУ, выраженные в паскалях (1 мм.вод.ст.  10 Па); V_в , V_г - соответственно объемные расходы рабочего тела на рассматриваемом участке ГТУ, м³/сек; _к и _т соответственно кпд осевого компрессора и газовой турбины.

Выражение удельной работы рассматриваемого цикла может быть сведено к виду [2]:

(1.27)

Функция h_e = h_e (_k) дважды обращается в нуль: один раз при  =1, второй раз при  = 1, т.е. когда  = ²_m (соотношение 1.24). Следовательно, уравнение (1.27) проходит через максимум.

Оценка состояния проточной части газотурбинной установки в целом может быть осуществлена, например, на основе сопоставления между собой температур реального процесса расширения по газовой турбине (_z = T₃ / T₄¹) - по компрессору (_с = Т₂¹ / Т₁₎ [ 17 ]:

(1. 28)

(1.29)

где коэффициенты - характеризуют потери давления соответственно в процессе подвода теплоты на участке тракта компрессор-турбина, потери давления на входе в осевой компрессор (на входном патрубке и фильтрах) и потери давления на выхлопе турбины (регенератор, утилизационные устройства, выхлопная труба); к^ - показатель внешнеадибатического (реального) процесса сжатия (расширения):

к = С_р /С_v (1. 30)

Коэффициент потерь работы в уравнении (1.30) – величина абсолютная , а знак перед ним соответствует знаку работы (плюс в процессах расширения, минус в процессах сжатия). Следовательно, показатель реального процесса расширения всегда меньше показателя адиабаты (к^  к ), показатель реального процесса сжатия всегда больше показателя адиабаты (к ^  к).

Анализ уравнения (1.29) показывает, что коэффициент суммарно определяет все виды потерь в цикле ГТУ, характеризует совершенство ее проточной части, а также отклонения от исходного состояния в результате загрязнения, коробления и т. п. численные значения этого коэффициента для регенеративных ГТУ и установок с развитой системой утилизации могут находиться в диапазоне 0, 90-0,93; для установок без регенерации теплоты отходящих газов на уровне 0,95-0,97. В процессе эксплуатации эти величины изменяются относительно слабо (Рис. 1. 9). Данные Рис. 1.9 на примере установки ГТ-750-6 в зависимости от наработки одновременно отражают и влияние относительных КПД осевого компрессора и газовой турбины на характеристику.

Как показывают данные Рис. 1.9, значительно большее влияние на изменение характеристики проточной части ГТУ, а следовательно и на характеристики агрегата в целом, оказывают изменения численных значений ее относительных КПД – осевого компрессора и газовой турбины.

Общее исходное выражение для относительных КПД осевого компрессора и газовой турбины можно записать в виде (верхние знаки для турбины, нижние для осевого компрессора):

(1.31)

или в форме:

(1.32)

Соотношение (1.32) известно как выражение политропного КПД турбомашин (верхние знаки для процесса расширения, нижние –для сжатия).

Между показателями реального процесса и внутренними относительными КПД компрессора (турбины) прослеживается четкая линейная зависимость (Рис. 1.10):

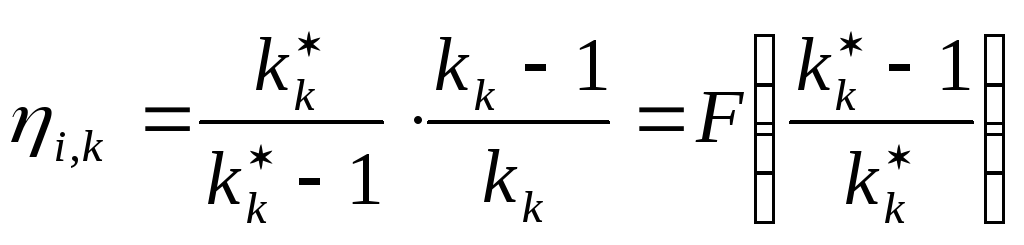(1.33)

(1.34)

Наличие графических зависимостей (Рис.1.10) между относительными КПД и показателями реальных процессов сжатия (расширения) дает возможность в эксплуатационных легко определять численные значения относительных КПД осевого компрессора и газовой турбины по показаниям штатных контрольно-измерительных приборов.

Определение показателей реальных процессов сжатия (расширения) осуществляется по уравнению политропы с переменным показателем:

(1.35)

отсюда

(1. 36)

где индексами «1» и «2» отмечены соответственно начальные и конечные параметры рабочего тела в процессе сжатия и расширения.

Численные значения относительных КПД осевого компрессора и газовой турбины, характеризующие степень совершенства процессов сжатия и расширения, а также изменение их в процессе эксплуатации, одновременно могут быть подсчитаны (как отмечалось выше) через соотношения соответствующих удельных работ в реальных процессах и соответствующих адиабатных перепадов процессов рабочего тела по компрессору (газовой турбине).

Зная изменение численных значений относительных КПД осевого компрессора и газовой турбины в процессе эксплуатации, относительно несложно, в частности, определить их влияние на относительное изменение КПД установки в целом.

Влияние изменения численных значений относительных КПД компрессора и газовой турбины на КПД установки в целом, а также изменение оптимального соотношения давлений сжатия по условию достижения максимального значения КПД ГТУ характеризуются данными Рис. 1.11, которые свидетельствуют о том, что увеличение численных значений КПД компрессора и турбины не только увеличивает значение КПД установки, но и осуществляет сдвиг оптимального соотношения давления сжатия в сторону больших значений.

Предположим, что относительные значения КПД осевого компрессора и газовой турбины в соотношении (1.31) изменились на величину . Тогда уравнение для определения удельной работы ГТУ после изменения относительного КПД на величинусоставит [ 12 ]:

(1.37)

Сопоставляя между собой соотношение (1.37) и аналогичное ему, но только без учета изменения численного значения относительного КПД осевого компрессора, получим:

(1.38)

Аналогичными рассуждениями можно оценить и влияние изменения КПД осевого компрессора на КПД установки в целом. Действительно, КПД установки определяется как отношение удельной работы агрегата к удельному количеству тепла, подведенного в камере сгорания на единицу количества поступившего воздуха:

(1.39)

где q– количество удельного тепла, подведенного в камере сгорания ГТУ на единицу количества поступившего воздуха при исходном значении КПД осевого компрессора:

(1.40)

где t₃ – температура газов на выходе из камеры сгорания (на входе в ТВД);t₂¹- температура воздуха на входе в камеру сгорания (в без регенеративных ГТУ – на выходе из осевого компрессора);- КПД камеры сгорания, величина довольно стабильная.

При изменении КПД осевого компрессора, уравнение (1.39) принимает вид:

(1.41)

Сопоставляя между собой соотношения (1.39) и (1.41) и полагая, что при незначительном изменении КПД осевого компрессора, расход топлива по камере сгорания остается неизменным, получим:

(1.42)

Аналогично, можно проследить и то, как будет изменяться КПД ГТУ при изменении относительного КПД газовой турбины. Действительно при исходном выражении КПД турбины, КПД установки имеет вид:

(1.43)

При изменении относительного КПД турбины, уравнение (1.43) принимает вид:

(1.44)

Сопоставляя между собой соотношения (1.43) и (1.44), получим:

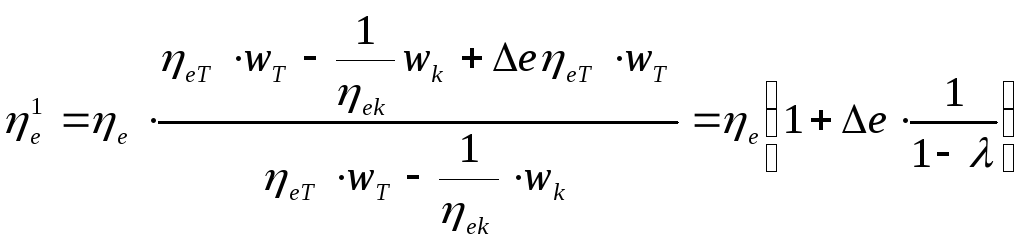(1.45)

где - во всех случаях представляет собой соотношение мощностей (работ) осевого компрессора и газовой турбины.

Если принять, к примеру, величину на уровне 0,01, то при= 0,67, соотношение (1.45) показывает, что КПД установки при этом увеличивается на 3%; при= 0,60 это увеличение составит 2,5% и т.д. Это свидетельствует о том, что чем меньше значение величины, тем меньше влияние изменения относительного КПД турбины на изменение КПД ГТУ и наоборот.

Примерно таким же соотношениям подчиняется и изменение удельной работы ГТУ при изменении относительных КПД турбины и осевого компрессора:

(1.46)

Следует также отметить, что влияние относительного изменения КПД турбины на мощность ГТУ несколько больше, чем в случае изменения относительного КПД осевого компрессора, а применительно к оценке экономичности двигателя это различие еще более ощутимо (Рис. 1.12).

В реальных циклах на его показатели большую роль играют температурные параметры (Т₁, Т₃и соотношение Т₃/Т₁).

При заданных величинах гидравлических сопротивлений по циклу и эффективности турбомашин, каждому значению температурной характеристики соответствует оптимальное значение параметров компрессора (), при котором эффективно-термодинамический КПД установки достигает максимума. Приведенные выше диаграммы (Рис. 1.8) показывают, что повышение температуры газов перед турбиной Т₃или понижение температуры воздуха перед компрессором Т₁ , что эквивалентно увеличению, приводит к неизменному и весьма существенном повышению КПД установки и ее удельной работы.

Задача 1.3. Определить основные показатели эффективно-термодинамического (реального) цикла газотурбинной установки простейшей схемы при следующих исходных данных: начальная температура воздуха на входе в осевой компрессор, t₁ = +15 ⁰C; температура продуктов сгорания на входе в газовую турбину, t₃ = 800 ⁰C; относительный адиабатический КПД осевого компрессора, = 0,85; относительный адиабатический КПД газовой турбины; приведенная характеристика сети, учитывающая влияние гидравлических сопротивлений, а также различие в средних теплоемкостях рабочего тела в процессах сжатия и расширения,; потери и служебные расходы воздуха, 1-m =0,05. Сама величина m определяется как отношение количества рабочего тела, проходящего через турбину к количеству рабочего тела, поступившего на сжатие; КПД камеры сгорания = 0,95; степень регенерации,= 0,80 .

Решение [3]. По уравнению (1.10) определяется соотношение граничных абсолютных температур цикла:

Произведение основных относительных коэффициентов полезного действия, характеризующих отличие реальных процессов от идеальных:

Приведенное (действительное) соотношение граничных абсолютных температур цикла (с учетом необратимых потерь):

Из уравнения (1.11а) определяется характеристика адиабатического расширения, соответствующая условию получения наибольшей удельной работы:

В целях упрощения результатов расчета в качестве рабочего рассматриваемого цикла рассматривает рассматривается сухой воздух.

Графическое отображение зависимости приводит к выводу, что при заданной степени регенерациихарактеристика адиабатического расширения в условиях энергетически наивыгоднейшего режима работы (составит:

Следовательно, средняя абсолютная температура рабочего тела (воздух) в процессе адиабатического расширения может быть определена соотношением:

Соответствующее значение теплоемкости рабочего тела С_рm,тур.= 1,1225 кДж/кг К;

Отсюда следует соотношение граничных давлений расширения по турбине:

Средняя абсолютная температура воздуха в процессе адиабатического сжатия:

Соответствующее значение теплоемкости воздуха в процессе, согласно соответствующим таблицам, составит: С_рm,ком = 1,0529 кДж/кгК.

Характеристика адиабатического сжатия с учетом приведенной характеристики сети составит:

Соответственно, соотношение граничных давлений сжатия (соотношение граничных давлений цикла):

По уравнению (1.9) определяется соотношение мощностей осевого компрессора и газовой турбины в энергетически наивыгоднейшем режиме цикла:

Удельная работа в энергетически наивыгоднейшем режиме:

Конечные абсолютные температуры рабочего тела в процессах расширения и сжатия:

Соотношение разностей температур, характеризующее возможности регенеративного использования тепла:

КПД эффективно-термодинамического цикла простейшего реального газотурбинной установки в условиях энергетически наивыгоднейшего режима работы в итоге составит:

В цикле наибольшей удельной работы средние температуры и основные показатели подсчитываются аналогично.

Результаты расчетов показывают, что в условиях регенеративного использования тепла энергетически наивыгоднейший режим работы имеет несомненные преимущества сравнительно с режимом наибольшей работы, в особенности в эксплуатационной нагрузке установок. Основная характеристика переменного режима работы играет особенно большую роль в стабилизации показателей рабочего процесса на частичных нагрузках и при ухудшении относительных КПД компрессора и газовой турбины.

Задача 1.4. Определить относительный адиабатический КПД осевого компрессора, работающих при следующих исходных данных: степень сжатия по компрессору равна 10; начальная температура процесса сжатия t₁=+15 ⁰C; конечная температура реального процесса сжатия t₂ =340 ⁰C.

При расчетах термодинамических циклов газотурбинных агрегатов с достаточно высокой степенью точности расчетов можно использовать соотношения законов идеальных газов (прежде всего в силу небольших соотношений давлений рабочего тела по тракту установки). При этом условии все параметры рабочего тела определяются только в функции температуры рабочего тела.

Относительный адиабатический КПД компрессора в этом случае определяется как отношение обратимой работы в процессе адиабатического сжатия к реальной работе в пределах заданных температур процесса.

где h_a и h_p – соответственно энтальпия в адиабатическом (обратимом) и реальном процессах сжатия, определяемые только как функции температуры процессов; С_pm и C¹_pm – средние теплоемкости а адиабатическом и реальном процессах сжатия. В силу стабильности теплоемкостей при таких уровнях температур, в расчете их можно принять численно равными; Т_а- конечная температура адиабатического процесса сжатия. Из уравнения адиабаты эта температура определяется соотношением:

Следовательно,

Задача 1.5. В результате проведенного ремонта проточной части газовой турбины (наплавка метала на концы лопаток, установка сотовых уплотнений и т.п.) относительный КПД газовой турбины увеличился на 2,4%, с величины 0,85 до величины 0,87: или на 2,4 %. Определить как это отразилось на изменение КПД и мощности установки в целом.

Решение. При заданных значениях относительных КПД компрессора и газовой турбины, выражение для внутреннего КПД установки записывается в форме (соотношение 1.43):

(а)

При изменении внутреннего относительного КПД турбины на величину , приведенное соотношение принимает вид:

(б)

Сопоставляя между собой соотношения (а) и (б) и принимая во внимание, что при изменении относительного КПД турбины удельный расход топлива по камере сгорания практически не изменяется, получим:

(в)

Последнее соотношение получили, разделив числитель и знаменатель на величину и введя в рассмотрение параметр, характеризующий соотношение удельных работ компрессора и газовой турбины, численная величина которого на номинальных режимах работы ГТУ изменяется в диапазоне 0,65-0,70. Следовательно, при, увеличение относительного КПД газовой турбины на 2,4% приведет к увеличению КПД установки в целом примерно на 4%.

Аналогичным соотношением определяется и изменение мощности установки при изменении относительного КПД газовой турбины.

Используя различные численные значения величин, входящих в соотношение (в), можно проследить как будет меняться КПД установки и при других исходных данных.