Министерство образования и науки,молодёжи и спорта Украины

ОДЕССКАЯ НАЦИОНАЛЬНАЯ МОРСКАЯ АКАДЕМИЯ

Кафедра физики и химии

Лабораторная работа № 3.3

ОПРЕДЕЛЕНИЕ СКОРОСТИ ЗВУКОВЫХ ВОЛН В ВОЗДУХЕ МЕТОДОМ ИНТЕРФЕРЕНЦИИ

(Указания к лабораторной работе)

Cоставил проф. Михайленко В.И.

Утверждено на заседании кафедры, протокол № 2 от 29 сентября 2011 г.

  

Одесса - 2011

Лабораторная работа № 3.3

Определение скорости звуковых волн методом интерференции

1. ТЕОРЕТИЧЕСКАЯ ЧАСТЬ

1.1. ОБЩАЯ ХАРАКТЕРИСТИКА ВОЛНОВЫХ ПРОЦЕССОВ

Тело, которое движется в упругой среде, тратит часть энергии, втягивая в колебательный процесс частицы окружающей среды, т.е. такое тело излучает энергию в виде волн.

Процесс распространения возмущений в просторанстве, который сопровождается переносом энергии, называется волной. Сначала приходят у колебание соседние частицы окружающей среды, которые находятся в контакте с поверхностью движущегося тела, а потом все более удаленные.

Упругие волны - процесс распространения в упругой среде механических деформаций. Различают два вида упругих волн - продольные и поперечные.

Продольными называются волны, в которых колебания частиц среды происходят в направлении распространения волны. Упругие продольные волны связаны с объемной деформацией упругой среды и потому могут возникать в любых средах - твердых, жидких и газообразных. Звуковая волна в воздухе или жидкости представляет собой пример продольных волн. В твердом теле звуковая волна может быть как продольной, так и поперечной.

Рис.1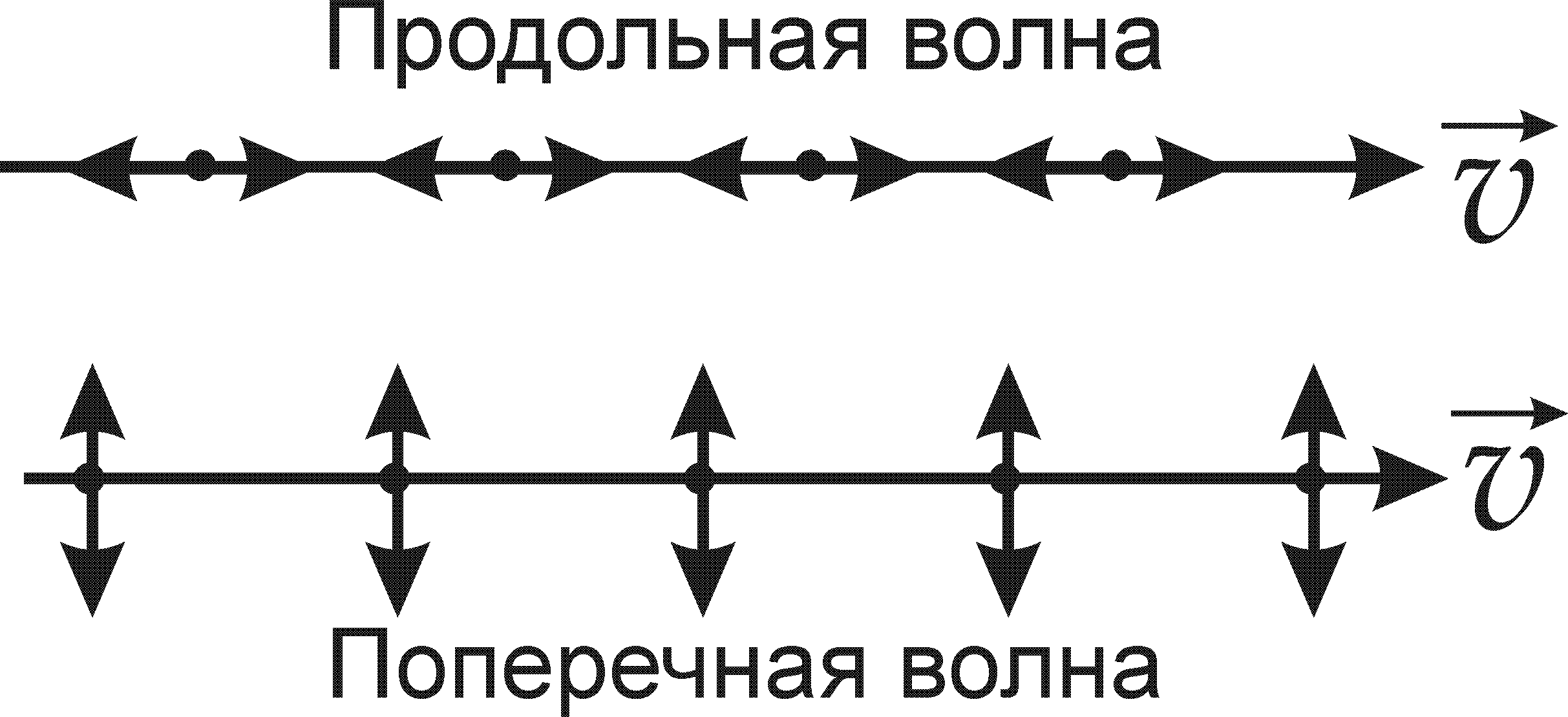

Поперечными называются такие волны, в которых колебания частиц среды происходят в направлении, перпендикулярном направлению распространения волны. Упругие поперечные волны могут распространяться лишь в средах, которые имеют упругую деформацию сдвига, т.е. в твердых телах. Поэтому в жидкостях и газах поперечные волны возникать не могут. Примером поперечных волн являются звуковые волны в твердом теле, колебания струны, электромагнитные волны.

Схематично продольные и поперечные волны показаны на рис.1.

1.2. Уравнение бегущей волны

Выведем уравнение одномерной упругой волны, которую называют часто бегущей волной. Пусть в некоторой точке О (рис. 2) в упругой среде находится источник волн, который выполняет колебания по закону:

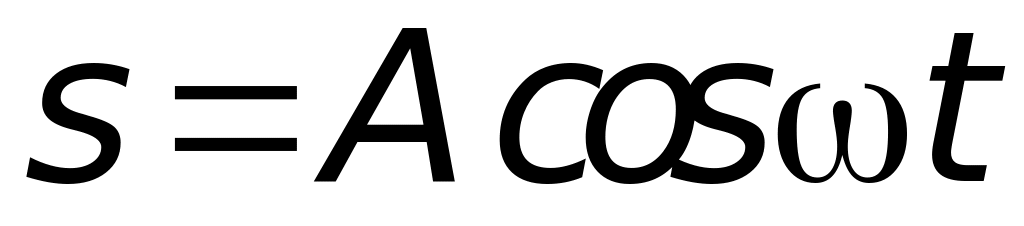
(1)

Рис.2

Очевидно, что частица среды, которая находится на расстоянии х от источника волн, начнет колебания только тогда, когда к ней дойдет волновой процесс, который распространяется в среде, т.е. колебание рассмотренной нами частицы будут происходить по закону (1), но с опозданием на промежуток времени

,

где v – скорость распространения волны.

Таким образом, колебания частицы, которая находится в точке М, будут происходить по закону

или

(2)

Здесь – сдвиг частицы в точке пространства с координатой x в момент времени t.

Уравнение (2) представляет собой уравнение бегущей волны. Из этого уравнения видно, что сдвиг частицы среды является периодической функцией как пространственной, так и временной координаты.

Аргумент косинуса в (2) представляет собой фазу волны.

Кратчайшее расстояние между точками, которые колеблются в одинаковой фазе, называется длиной волны. Длина волны численно равняется расстоянию, на которое распространяется волна за время, равное периоду колебаний:

,

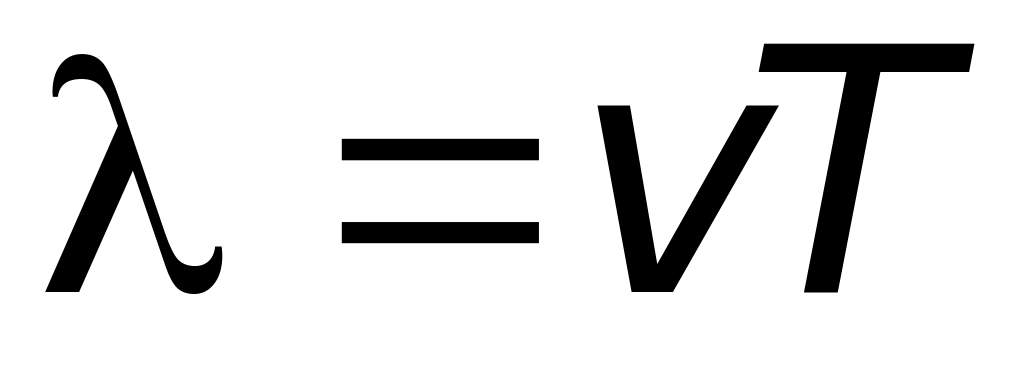(3)

где – период колебаний, – скорость распространения волны.

Преобразуем фазу волны таким образом:

.

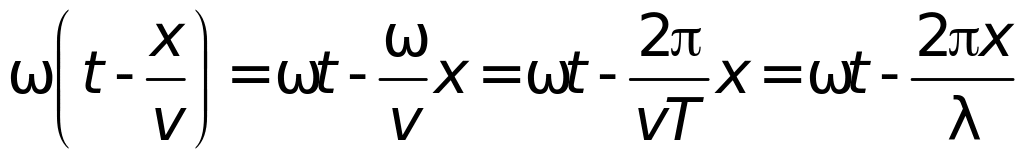(4)

С учетом (4) уравнение волны (2) можно представить в виде:

.

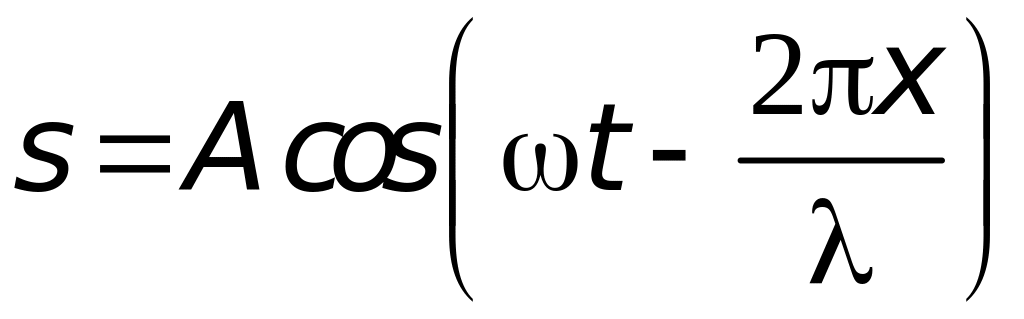(5)

1.3.Интерференция волн

Рис. 3

Интерференцией называется явление наложения когерентных волн, в результате которого происходит пространственное перераспределение интенсивности, – возникает система интерференционных максимумов и минимумов.

Когерентными называются такие волны, которые имеют одинаковую частоту и не зависящую от времени разность фаз.

Рассмотрим простейший случай сложения двух когерентных волн, которые создаются в упругой среде двумя источниками и (рис. 3).

Волна от источника вызывает в некоторой точке М смещение

,

(6)

а от источника

.

(7)

В результате частица будет одновременно брать участие в двух гармонических колебаниях одинакового направления и одинаковой частоты. При этом ее смещение, очевидно, будет равняться сумме: . Результирующее колебание также будет гармоническим с амплитудой, равной

.

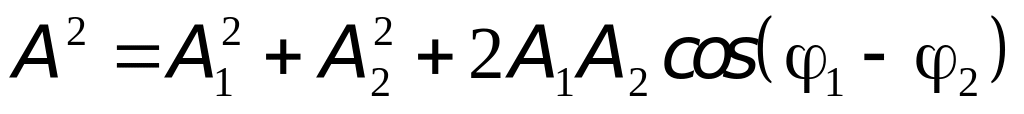(8)

где – разность фаз, которую можно найти с помощью (6) и (7):

.

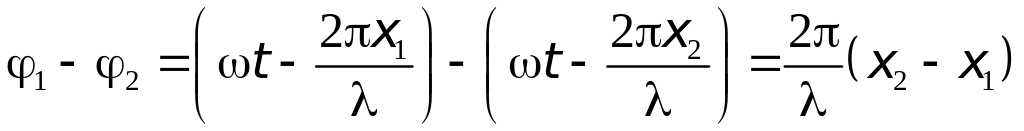(9)

В выражении (9) величина х₂- х₁ называется разностью хода.

С учетом (9) выражение (8) можно представить в виде:

.

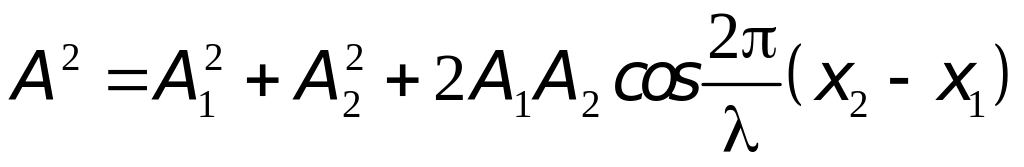(10)

Рассмотрим частные случаи.

1. Пусть разность хода равняется чётному числу длин полуволн

.

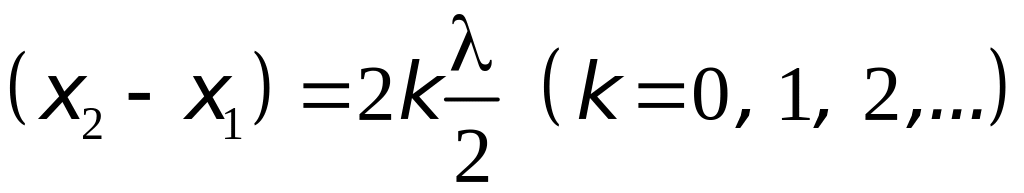Тогда

,

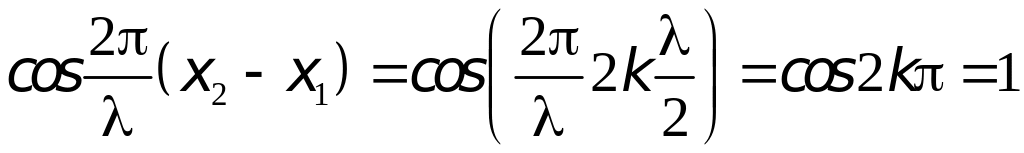поэтому:

.

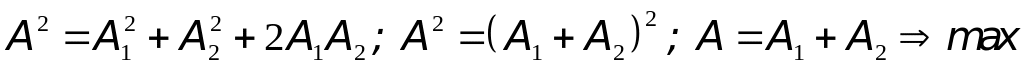(11)

Из выражения (11) видно, что результирующая амплитуда равняется сумме амплитуд, т.е. в этом случае возникает интерференционный максимум. Таким образом, условие возникновения интерференционных максимумов можно сформулировать таким образом:

ИНТЕРФЕРЕНЦИОННЫЕ МАКСИМУМЫ НАБЛЮДАЮТСЯ ДЛЯ ТАКИХ ТОЧЕК ПРОСТРАНСТВА, ГДЕ РАЗНОСТЬ ХОДА РАВНЯЕТСЯ ЧЁТНОМУ ЧИСЛУ ДЛИН ПОЛУВОЛН.

В этом случае волны встечаются с одинаковой фазой и взаимно усиливают друг друга.

2. Аналогично можно показать (докажите это!), что когда разность хода равняется нечётному числу длин полуволн, т.е.

,

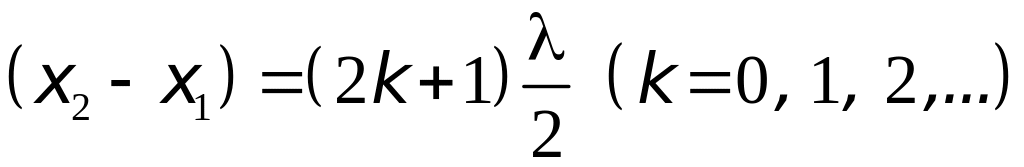то результирующая амплитуда колебаний равняется:

.

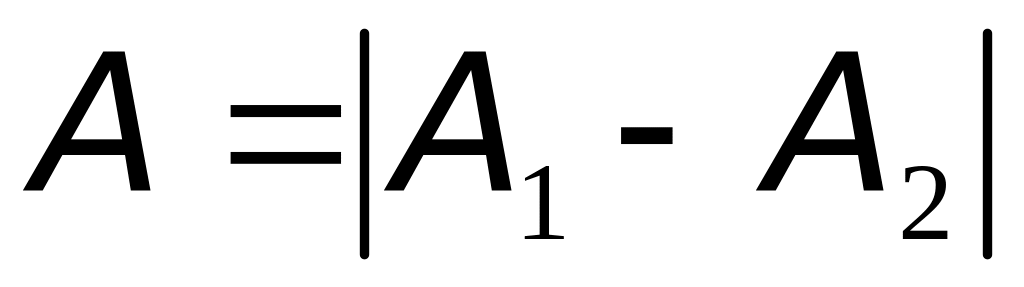В частности, если , то , т.е. для таких точек пространства наблюдается полное гашение волн, которые накладываются.

Итак, ИНТЕРФЕРЕНЦИОННЫЕ МИНИМУМЫ НАБЛЮДАЮТСЯ ДЛЯ ТАКИХ ТОЧЕК ПРОСТРАНСТВА, ГДЕ РАЗНОСТЬ ХОДА РАВНЯЕТСЯ НЕЧЁТНОМУ ЧИСЛУ ДЛИН ПОЛУВОЛН.

В этом случае волны встечаются с противоположной фазой и взаимно ослабляют друг друга.