Министерство образования и науки, молодёжи и спорта Украины

ОДЕССКАЯ НАЦИОНАЛЬНАЯ МОРСКАЯ АКАДЕМИЯ

Кафедра физики и химии

Лабораторная работа № 3.2

ВЫНУЖДЕННЫЕ КОЛЕБАНИЯ

(Указания к лабораторной работе)

Cоставил проф. Михайленко В.И.

Утверждено на заседании кафедры, протокол № 2 от 29 сентября 2011 г.

Одесса - 2011

Лабораторная работа № 3.2

ВЫНУЖДЕННЫЕ КОЛЕБАНИЯ

1. ТЕОРЕТИЧЕСКАЯ ЧАСТЬ

1.1. ОБЩАЯ ХАРАКТЕРИСТИКА КОЛЕБАНИЙ

Колебаниями называются движения или процессы, которые характеризуются той или другой степенью повторяемости во времени.

Колебания называются периодическими, если значения всех физических величин, которые характеризуют колебательную систему, повторяются через равные промежутки времени.

Время осуществления одного полного колебания называется периодом колебания – Т.

Частотой периодических колебаний называется величина  =1/Т, равная числу полных колебаний за единицу времени. Единица измерения частоты -1 Герц - одно полное колебание за 1 секунду.

Циклической частотой периодических колебаний называется величина =2=2/Т, равная числу полных колебаний за 2 секунд.

Периодические колебания величины x(t) называются гармоническими, если она изменяется по закону синуса или косинуса.

В дальнейшем мы будем рассматривать гармоничные колебания, которые изменяются по закону косинуса

(1)

Здесь _o – циклическая частота гармонических колебаний; -амплитуда колебаний, т.е. максимальное по модулю значение колебательной величины x; – фаза; – начальная фаза колебаний.

Зная фазу колебаний, можно определить величину смещения x в данный момент времени. Начальная фаза колебаний показывает величину смещения от положения равновесия в начальный момент времени, т.е. при :

1.2. Сложение гармоничных колебаний одинакового направления

Рис. 1.

Решение ряда вопросов облегчается, если изображать колебание графически в виде векторов на плоскости. Полученная таким образом схема называется векторной диаграммой.

Из точки О, взятой на оси , проведем вектор , который образует с осью угол . Проекция этого вектора на ось x равняется (рис.1):

Предположим теперь, что вектор равномерно вращается с угловой скоростью _o. Тогда за время он опишет угол и его новая проекция на ось станет:

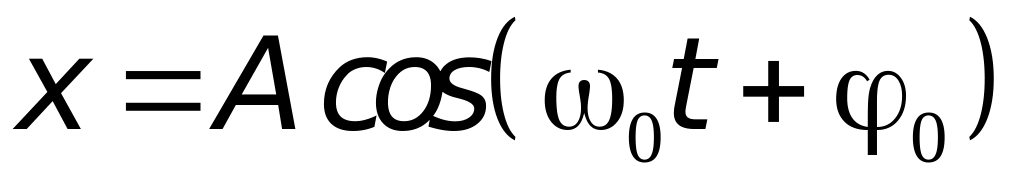
(2)

Таким образом, проекция конца вектора на ось будет выполнять гармонические колебания с амплитудой, равной длине вектора , с частотой ₀ , равной угловой скорости вращения вектора, и с начальной фазой ₀, равной углу, образованному вектором с осью х в начальный момент времени.

Рассмотрим сложение двух гармонических колебаний одинакового направления и одинаковой частоты:

Рис. 2.

Представим оба колебания с помощью векторов А₁ и А₂, которые образуют с оссю х углы и соответственно (рис. 2). Построим по правилу сложения векторов результирующий вектор. Из рис. 2 видно, что проекция этого вектора на ось х равняется сумме:

Вектор А_р вращается с той же угловой скоростью _o, что и векторы А₁ и А₂, поэтому результирующее колебание будет гармоническим с частотой _o, амплитудой А_р и начальной фазой :

Найдем теперь из векторной диаграммы (см. рис. 2) результирующую амплитуду А_р. Из заштрихованного треугольника по теореме косинусов имеем:

(3)

1.3. Вынужденные колебания

В реальных условиях колебательная система постепенно теряет энергию на преодоление сил трения. В результате, колебания являются затухающими. Чтобы колебания были незатухающими, необходимо каким-то образом подводить к колебательной системе энергию, пополняя ее потери.

Предположим, что на колебательную систему действует внешняя (вынуждающая) сила, которая изменяется по гармоническому закону:

,

(4)

где  – циклическая частота, а – амплитудное значение силы.

Для наглядности будем считать, что колебательная система представляет собой пружинный маятник, который выполняет колебания в вязкой среде (рис. 3). Тогда на закрепленное к пружине тело будет действовать возвращающая сила, которая по своей природе является упругой силой F_упр, и сила сопротивления F_сопр. По закону Гука

,

где x – смещение от положения равновесия (абсолютная деформация), а k – квазиупругая постоянная (в данном случае жесткость пружины).

При малых скоростях сила сопротивления пропорциональна скорости

,

(5)

где – коэффициент сопротивления, который зависит от формы тела и вязкости среды.

Таким образом, результирующая сила, которая действует на тело, равняется сумме квазиупругой силы, силы сопротивления и вынуждающей силы:

.

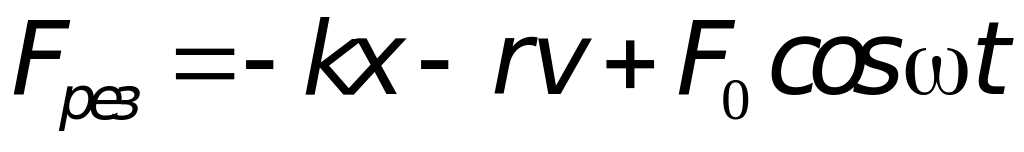Составим уравнение движения, используя второй закон Ньютона ( ):

.

Принимая во внимание, что a=d²x/dt², v=dx/dt, поделив это уравнение на массу и обозначив ( – коэффициент затухания), получим дифференциальное уравнение вынужденных колебаний:

.

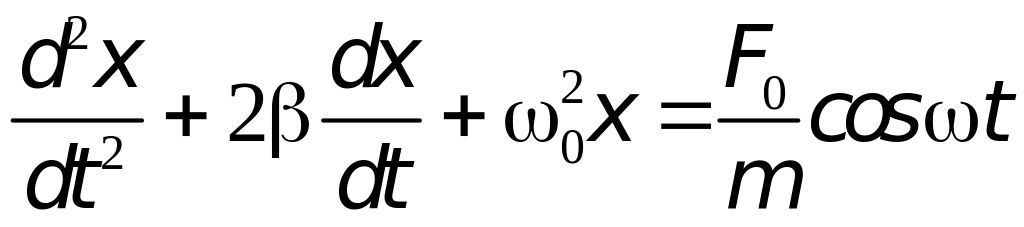(6)

Здесь _o – собственная частота незатухающих колебаний

Решение этого уравнения будем искать в виде:

,

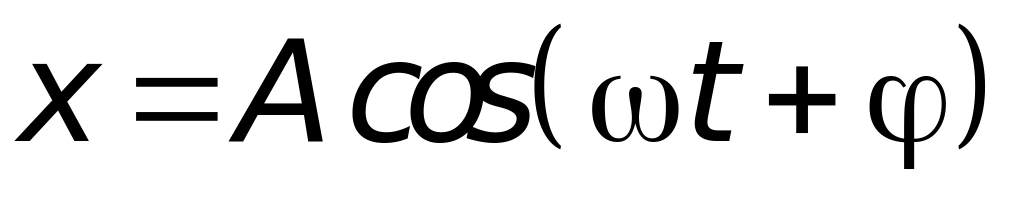(7)

т.е. мы считаем, что система выполняет колебания с частотой, равной частоте колебаний внешней силы.

Для нахождения амплитуды А вынужденных колебаний продифференцируем (7) дважды по времени и подставим в (6). Имеем

	(8)
	(9)

Подставляя (7-9) в (6), получим:

или

(10)

Из выражения (10) видно, что в результате сложения двух гармоничнских колебаний, сдвинутых по фазе на , получается гармоническое колебание с амплитудой и начальной фазой, равной нулю. При сложении двух гармонических колебаний одинаковой частоты и одинакового направления результирующая амплитуда колебаний может быть найдена по формуле (3). В данном случае

(11)

Подставляя эти выражения в формулу (3), получим:

отсюда

.

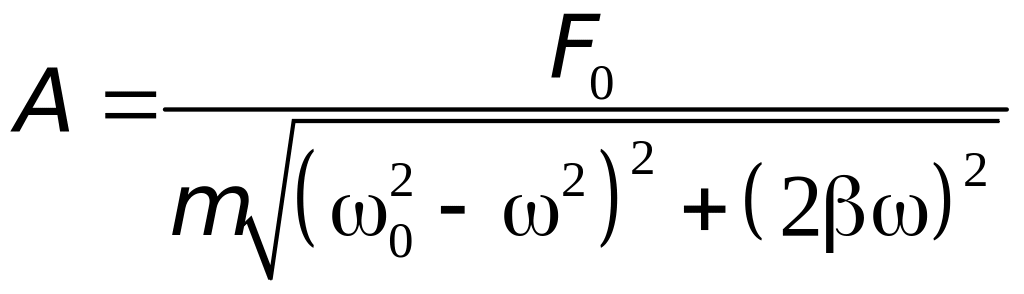(12)

Из выражения (12) видно, что амплитуда вынужденных колебаний зависит от частоты внешней периодически действующей силы. При ; если же , то . График зависимости от при двух разных коэффициентах затухания представлен на рис. 4. При некотором значении амплитуда вынужденных колебаний достигает максимального значения. Явление резкого возрастания амплитуды вынужденных колебаний, когда частота внешней периодически действующей силы приближается к , называется резонансом. Частота , при которой наступает резонанс, называется резонансной. Значение можно найти из условия, что при амплитуда . Это условие выполняется, если подкоренное выражение в (12) при будет минимальным. Это означает, что первая производная по частоте от подкоренного выражения равняется нулю:

Отсюда после несложных преобразований находим:

.

(13)

Резонансное значение амплитуды получим, если подставить (13) в (12):

Рис. 3.

. (14)

Видно, что чем меньше коэффициент затухания , тем больше (рис. 3). В ряде случаев резонанс может стать опасным явлением, которое вызывает разрушение колебательной системы, вследствие чрезмерного роста амплитуды.