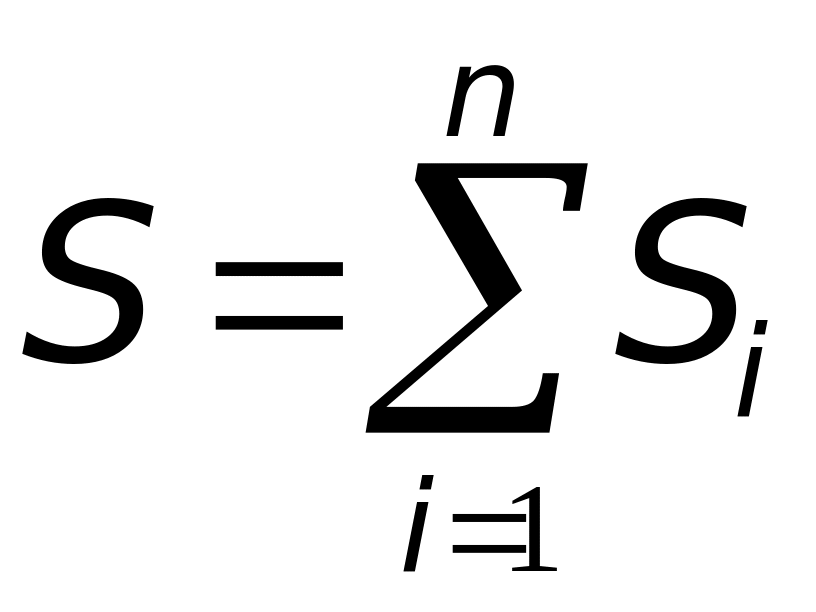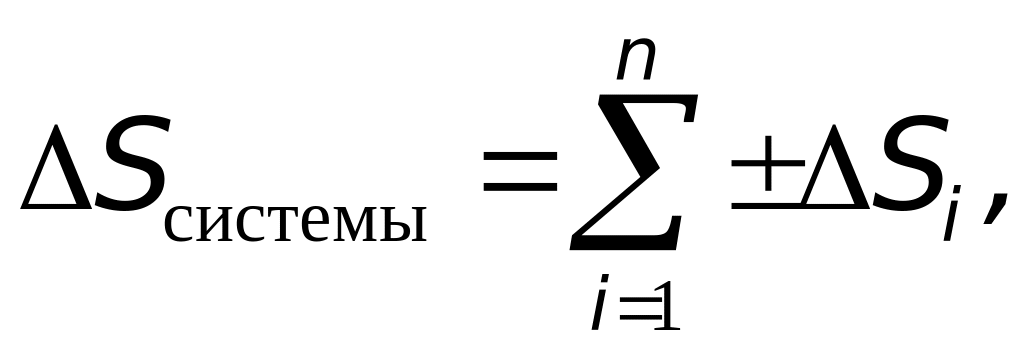Министерство образования и науки, молодежи и спорта Украины
Одесская национальная морская академия
Кафедра физики и химии
Лабораторная работа № 2.2 Определение изменения энтропии в необратимых процессах теплообмена
(Указания к лабораторной работе)
Составили: доц. Шакун К.С.,
проф. Михайленко В.И.
Утверждено на заседании кафедры
протокол №2 от 29 сентября 2011 г.
Одесса - 2011
1.Теоретическая часть
1. Термодинамической системой называется совокупность макроскопических физических тел, которые могут обмениваться энергией в форме выполнения механической работы и передачи теплоты, как между собой, так и с окружающей средой.
2. Различают открытые термодинамические системы, для которых нет никаких ограничений в обмене энергией с окружающей средой, и частично замкнутые системы: а) механически замкнутые, не могут обмениваться энергией с окружающей средой в форме выполнения работы; б) адиабатно замкнутые, которые не могут обмениваться теплотой с окружающей средой.
3. Состояние термодинамической системы определяется значениями ряда макроскопических параметров (например, P, V, Т) и функциями состояния (такими, как полная энергия термодинамической системы, внутренняя энергия системы, энтропия и другие).
4. Термодинамически равновесным состоянием системы называется такое состояние, в котором макроскопические параметры состояния одинаковы во всех частях термодинамической системы и не изменяются во времени.
5. Термодинамическим процессом называется любое изменение состояния системы, связанное с изменением ее термодинамических параметров.
6. Термодинамические процессы могут быть обратимыми и необратимыми. Обратимым процессом называется такой равновесный процесс, который предполагает возможность самопроизвольного возвращения системы в исходное состояние без того, чтобы в окружающей среде остались какие-либо изменения. Обратимые процессы – идеализированные, примером их могут служить такие процессы, как незатухающие гармонические колебания или абсолютно упругие удары тел. Все реальные процессы – необратимы, так как они сопровождаются потерями на выполнение работы против сил трения, тепловыми потерями, т.д. Каждый необратимый процесс в одном направлении протекает самопроизвольно, а для того, чтобы провести его в обратном направлении необходимо осуществить некоторый дополнительный компенсирующий процесс.
7. Одной из важных функций, описывающих состояние термодинамической системы, является энтропия. Элементарное изменение энтропии dS определяется отношением бесконечно малого количества теплоты dQ, сообщаемой термодинамической системе, к ее абсолютной температуре Т при обратимом процессе.
|
(1) |
Полное значение энтропии системы равно
|
|
и не зависит от способа, которым система пришла в это состояние (здесь S0 – произвольная постоянная).
Энтропия является аддитивной величиной, т.е. энтропия системы равна сумме энтропий тел, входящих в систему,
|
(2) |
и аналогично изменение энтропии системы равно
|
|
где n - количество тел, входящих в систему.
Энтропия принципиально отличается от других термодинамических функций направленностью своей смены:
Энтропия адиабатно изолированной системы остается неизменной во всех обратимых процессах и возрастает в необратимых процессах (это второй закон термодинамики)
|
|
Рост энтропии происходит до некоторого максимального значения, что соответствует состоянию термодинамического равновесия, после чего значение энтропии остается постоянным.
Все термодинамические процессы осуществляются системой только в соответствии с первым законом термодинамики.
Тепло dQ, которое было сообщено термодинамической системе, расходуется на выполнение механической работы dA против внешних сил и на изменение внутренней энергии системы dU
|
(3) |
Используя формулу (1), получаем
|
(4) |
После интегрирование (4) при постоянной температуре находим
|
(5) |
Откуда, обозначив
![]() ,
запишем
,
запишем
|
(6) |
где F – свободная энергия термодинамической системы, т.е. та часть внутренней энергии, которую можно целиком превратить в механическую работу при изотермическом процессе (T = const), TS – связана энергия, представляет собой ту часть внутренней энергии, которую невозможно превратить в работу при Т = const. Отсюда вытекает определение энтропии как меры связанной энергии термодинамической системы, которую превратить в механическую работу невозможно.
Рассмотрим энтропию с точки зрения молекулярно-кинетической теории на примере идеального газа. Внутренняя энергия идеального газа равна сумме кинетических энергий молекул, движутся хаотически. Доля внутренней энергии идеального газа в виде свободной энергии F представляет собой ту часть энергии, которая может быть преобразована в энергию направленного движения при постоянной температуре. Внутренняя энергия идеального газа в виде связанной энергии TS представляет собой ту часть энергии хаотического движения, которое нельзя превратить в энергию направленного движения. При этом, чем больше энтропия системы, тем большую часть внутренней энергии невозможно превратить в энергию направленного движения. Поэтому можно сказать, что энтропия является мерой хаотичности системы.