
- •Лабораторная работа № 1.4 изучение вращательного движения твердого тела
- •1. Теоретическая часть
- •1.2. Основной закон динамики вращательного движения
- •2. Приборы и принадлежности
- •3. Экспериментальная установка
- •4. Вывод расчётной формулы
- •5. Порядок проведения измерений
- •6. Обработка результатов измерений
- •7. Рекомендации к оформлению отчета
- •8. Контрольные вопросы
- •9. Литература
Министерство образования и науки, молодёжи и спорта Украины
ОДЕССКАЯ НАЦИОНАЛЬНАЯ МОРСКАЯ АКАДЕМИЯ
Кафедра физики и химии
ЛАБОРАТОРНАЯ РАБОТА № 1.4
ИЗУЧЕНИЕ ВРАЩАТЕЛЬНОГО ДВИЖЕНИЯ ТВЕРДОГО ТЕЛА
(указания к лабораторной работе)
Составил проф. Михайленко В.И.
Утверждено на заседании кафедры, протокол № 2 от 29 сентября 2011 г.

Одесса-2011
Лабораторная работа № 1.4 изучение вращательного движения твердого тела
1. Теоретическая часть
1.1 Аналогия между поступательным и вращательным движением
Поступательное движение |
Вращательное движение |
||
1. Поступательным называется такое движение, при котором все точки тела описывают одинаковые по форме траектории. |
1. Вращательным называется такое движение, при котором все точки тела описывают окружности, центры которых лежат на одной и той же прямой (ось вращения). |
||
2. Путь
|
2. Угол φ, который описывает радиус-вектор за некоторое время. |
||
3. Линейная скорость численно равняется пути, пройденному материальной точкой за единицу времени. Она определяется как первая производная от пути по времени
Вектор линейной скорости совпадает с касательной в данной точке траектории и направлен в сторону движения (рис.1.1).
Рис.1.1 |
3. Угловая скорость численно равняется углу поворота радиус-вектора за единицу времени. Она определяется как первая производная от угла поворота по времени
Вектор угловой скорости находится по правилу правого буравчика: необходимо установить буравчик вдоль оси вращения и крутить его в направлении вращения; тогда поступательное движение буравчика укажет на направление угловой скорости (рис.1.1а).
Рис.1.1а Заметим,
что вектор
|
||
4. Линейное ускорение численно равняется изменению скорости за единицу времени. Оно определяется как первая производная от скорости по времени
Пример.
Материальная точка движется по закону
Решение:
|
4. Угловое ускорение численно равняется изменению угловой скорости за единицу времени. Оно определяется как первая производная от угловой скорости по времени
Пример.
Тело вращается по закону
Решение:
|
||
5. Свойство тел сохранять состояние покоя или равномерного прямолинейного движения называется инертностью. Масса (m) – мера инертности тела при поступательном движении. |
5. Свойство тел сохранять состояние покоя или равномерного вращательного движения называется инертностью. Момент инерции (I) – мера инертности тела при вращательном движении. Момент инерции зависит от массы и формы тела, а также от выбора оси вращения. Момент инерции материальной точки определяется как произведение массы точки на квадрат расстояния до оси вращения:
В общем случае момент инерции тела произвольной формы находят по формуле
где N – количество материальных точек, на которое разбивается тело. Момент инерции тонкого кольца, вдвое больше момента инерции сплошного диска (рис.2):
Ось вращения, которая проходит через центр масс тела, называется собственной осью. Момент инерции относительно собственной оси называется собственным моментом инерции. Момент инерции относительно произвольной оси, параллельной оси собственного вращения, можно рассчитать с помощью теоремы Штейнера: момент инерции тела относительно произвольной оси, параллельной собственной оси, равняется собственному моменту инерции плюс произведение массы тела на квадрат расстояния между осями:
где I0 - собственный момент инерции, т.е. момент инерции относительно оси СС (рис. 1.3), а I - момент инерции относительно оси ОО.
Рис.1.3 |
||
Сила – мера взаимодействия тел, вследствие чего появляется ускорение или деформация тел. |
Момент силы – это
произведение силы на плечо:
Момент
силы – вектор, направление которого
устанавливается по правилу буравчика.
В данном случае (рис.1.4) вектор
|
||
Произведение силы
на время ее действия –
Произведение
массы тела на его скорость –
|
Произведение момента
силы на время его действия – Произведение
момента инерции на угловую скорость
–
|
||
Второй закон Ньютона: Ускорение, с которым движется тело, пропорционально приложенной силе и обратно пропорционально его массе:
Если
учесть, что
Импульс силы равняется изменению импульса тела. |
Основной закон динамики вращательного движения: Угловое ускорение, с которым вращается тело, пропорционально моменту силы и обратно пропорционально его моменту инерции:
Если
учесть, что
Импульс момента силы равняется изменению момента импульса тела. |
||
Кинетическая энергия поступательного движения определяется формулой
|
Кинетическая энергия вращательного движения определяется формулой
|





 ,
,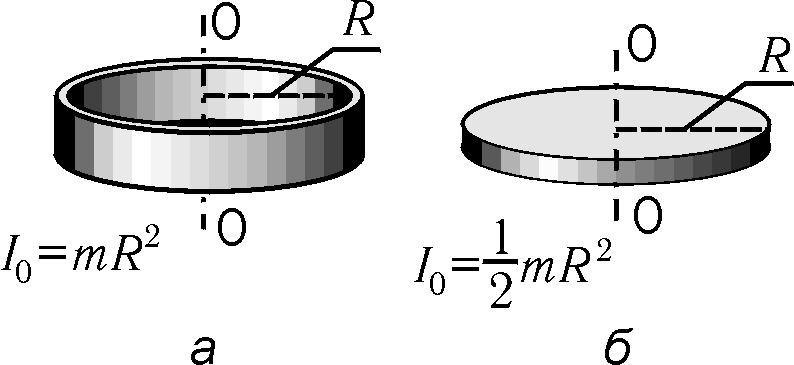 Рис.1.2
Рис.1.2
 Рис.1.4.
Рис.1.4.