ЛАБОРАТОРНА РОБОТА №4. ВКЛАДЕНІ АРИФМЕТИЧНІ ЦИКЛІЧНІ ОБЧИСЛЮВАЛЬНІ ПРОЦЕСИ
Мета: вивчення основ побудови алгоритмів та основних операторів, які використовуються для вирішення задач з циклічною структурою.
Порядок виконання лабораторної роботи:
1 – провести лабораторне дослідження на тестовому прикладі;
2 – виконати індивідуальні завдання;
3 – оформити результати досліджень в журналі.
Теоретичний матеріал
Так як кожний цикл можна класифікувати за трьома ознаками, розглянемо вкладені арифметичні циклічні обчислювальні процеси з перед або після умовою.
Арифметичні цикли з одним параметром називаються простими, з декількома – вкладеними. Вкладеним називається цикл, що містить у собі один або кілька інших циклів. Цикл, що охоплює інші цикли, називається зовнішнім, а інші - внутрішніми.
Кількість повторень обчислюється як добуток кількості повторень всіх простих циклів.
Типи задач:
табулювання функції декількох аргументів - обчислити значення функції в заданих точках, якщо функція має декілька аргументів;
накопичувачі - ∑, ∏ (!), де розрахунок елементу ряду залежить від декількох параметрів (лічильників) циклів.
Розглянемо задачі табулювання функції декількох аргументів:
§
І етап – формалізація задачі.
ІІ етап – алгоритмізація.
Т
ехнологія
проектування вкладеного арифметичного
циклу для задачі табулювання функції
включає:
1 – задати початкове значення першому параметру циклу;
2 – перевірити умову закінчення циклу - чи входить значення першого параметра циклу в інтервал його зміни;
3 – задати початкове значення другому параметру циклу;
4 – перевірити умову закінчення циклу - чи входить значення другого параметра циклу в інтервал його зміни;
5 – здійснити задані обчислення функції і вивести результати;
6 – змінити другий параметр циклу на величину кроку;
7 – повернутися до перевірки умови закінчення внутрішнього циклу, якщо цикл завершено, виконати 8,9.
8 – змінити перший параметр циклу на величину кроку;
9 – повернутися до перевірки умови закінчення зовнішнього циклу.
Умовні позначення символів (блоків) та функції, які відображаються ними як і у простому циклу.
Кількість повторень тестової задачі обчислюється за формулою:
Кількість повторень = КПЗЦ * КПВЦ = 3 * 3 = 9
де КПЗЦ – кількість повторень зовнішнього циклу
КПВЦ – кількість повторень внутрішнього циклу
якщо КПЗЦ = ( КЗ – ПЗ ) \ КРОК + 1 = (3 – 1) \ 1 + 1 = 3
КПВЦ = ( КЗ – ПЗ ) \ КРОК + 1 = (2 – 1) \ 0.5 + 1 = 3
де ПЗ – початкове значення лічильника;
КЗ – кінцеве значення лічильника;
КРОК – крок змінення лічильника.
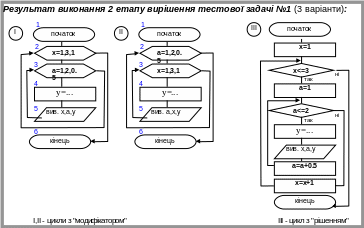
ІІІ етап – програмування.
ІV етап – тестування.
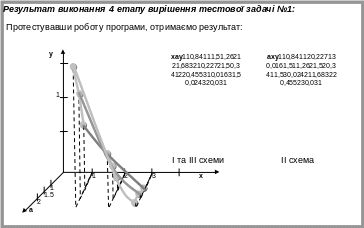
V етап – аналіз результатів.
Х
Х
Розглянемо задачі накопичення:
І етап – формалізація задачі.
Цикл в задачах накопичення є вкладеним, якщо процес накопичення (розрахунок елементу ряду) залежить від декількох лічильників. Глибина вкладеності алгоритму не обмежується. Обмеження можуть з'явитися при написанні програм із недостатніми можливостями використаної системи програмування.
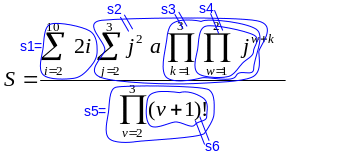
Розкладемо формулу на складові:
s1 – простий цикл;
s2, s3, – формують складну структуру (s2 – зовнішній по відношенню до s3,
s3 – зовнішній по відношенню до s2);
s5, s6 – формують складну структуру (s5 – зовнішній по відношенню до s6
s6 – внутрішній цикл).
ІІ етап – алгоритмізація та ІІІ етап – програмування.
Технологія проектування вкладеного арифметичного циклу для задач накопичення аналогічна технології проектування простого арифметичного циклу. Вкладені цикли повинні мати уніфіковані ідентифікатори параметрів, які закриваються у зворотному порядку.
Якщо кілька циклів мають одну загальну кінцеву точку, то можна вказати для них один оператор NEXT, перелічивши в ньому параметри циклів у порядку, зворотному їхній вкладеності (від внутрішніх - до зовнішнього).
Наприклад: FOR A=1 TO 3 FOR A=1 TO 3
FOR B=5 TO 14 FOR B=5 TO 14
C=A+B C=A+B
PRІNT C PRІNT C
NEXT B NEXT B, A
NEXT A
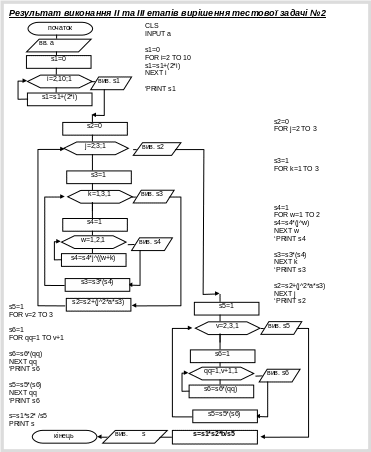
ІV етап – тестування.
