Приклад виконання завдання к2

За заданим рівнянням прямолінійного руху вантажу 1 визначити швидкість, обертальне, доцентрове і повне прискорення точки М механізму (рис.К.2) в той момент часу, коли шлях, пройдений вантажем, дорівнює S=0,3 м.

Дано: R₂=30 см, r₂=15 см, R₃=40 см, r₃=20 см, x=90t² см.

Розв’язання. Тіло 1 здійснює поступальний рух, а тіла 2 і 3 – обертальні рухи. Знайдемо швидкість вантажу 1 (рис. К.2) .

Оскільки трос нерозтяжний, то швидкість точки К колеса 2 дорівнює швидкості вантажу V₁. Тоді, кутова швидкість тіла 2 визначиться за формулою

.

Кутову швидкість колеса 3 знайдемо за співвідношенням . Звідси

.

Кутове прискорення тіла 3 визначимо за формулою

.

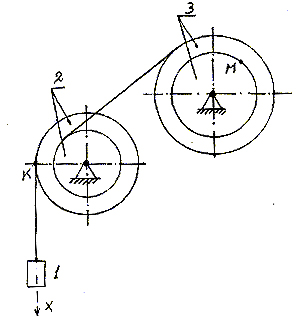
Рис К.2 Рис К.2'

Швидкість точки М дорівнює

.

Вектор швидкості напрямлений перпендикулярно до радіуса r₃ в сторону обертання колеса 3 (рис. К.2').

Обертальне і доосьове прискорення точки М визначимо за формулами

Вектор обертального прискорення співпадає за напрямом з вектором швидкості , оскільки обертання коліс прискорене, оскільки ω і ε мають однакові знаки. Вектор доосьового прискорення напрямлений по радіусу від точки М до центра колеса 3.

Повне прискорення точки визначимо за формулою

.

Визначимо момент часу τ, коли шлях S, пройдений вантажем 1, дорівнює 30 см:

Звідки

Значення всіх кінематичних характеристик руху точки М для моменту часу =0,58 c будуть відповідними: ; ; ; .

Відповідь: см/с; см/с; см/с; см/с.

Вектори швидкості і прискорень точки М показані на рис. К.2'.

Завдання К3. ВИЗНАЧЕННЯ ОСНОВНИХ КІНЕМАТИЧНИХ ХАРАКТЕРИСТИК ПЛОСКОГО РУХУ ТВЕРДОГО ТІЛА. КІНЕМАТИЧНИЙ АНАЛІЗ ПЛОСКОГО МЕХАНІЗМУ.

Для заданого положення механізму знайти швидкість точки С і прискорення точки В, а також кутову швидкість і кутове прискорення ланки, яка робить плоский рух. Схеми механізмів показані на рис. 2, необхідні дані наведені в таблиці 3.

Необхідно знати:

1. Формулу, що визначає швидкість точки М твердого тіла, яке робить плоский рух.

2. Поняття миттєвого центру швидкостей (м.ц.ш.).

3. Теорему про проекції швидкостей двох точок плоскої фігури.

4. Теорему про прискорення точок плоскої фігури.

Необхідно вміти:

1. Класифікувати рухи ланок плоского механізму.

2. Визначати положення миттєвого центру швидкостей ланки, що робить плоский рух, як м.ц.ш. плоскої фігури.

3. Використовувати поняття м.ц.ш. для визначення швидкостей точок плоскої фігури.

4. Аналітичне додавати вектори і визначати їх суму.

Приклад виконання завдання к3

Знайти швидкість точки В і прискорення точок В і Р рухомої шестерні радіуса r=0,05 м., яка котиться в середині нерухомої шестерні радіуса R=0,15 м. Шестерню радіуса r рухає кривошип, який обертається навколо осі О рівномірно з кутовою швидкістю =3 рад/с (рис. К.3).

Рис. К.3.

Д ано:

R=0,15 м

r=0,05 м

=3 рад/с

ОА=0,1м

-?

-?

-?