1. Ввести значения A, B, C, D.

2. Присвоить начальное значение I=0

3. Вычислить значение X=e^-a/b

4. Вычислить значение функции F=Cos²(X+A/B)…

5. Напечатать значение функции f.

6. Увеличить значение Х на значение шага, т.е. Х=Х+D

7. Увеличить значение параметра цикла I=I+1

8. Проверить значение I. Если I<=10, перейти к п.4, иначе окончание счета

Блок-схема циклического алгоритма для примера 6

Ввод

A,B,C,D

Рассмотрим еще один вариант организации циклического процесса.

Ниже приведена блок-схема вычисления функции

Y = X*LN(X) при X = 0.1; 0.4; 0.7 с указанием основных действий:

Словесный алгоритм:

1. Присвоить значение X=0,1 (задание начального значения параметра цикла)

2. Вычислить значение Y=XLn(X) (рабочий участок цикла – тело цикла)

3. Напечатать значение функции Y(рабочий участок цикла – тело цикла)

4. Х=Х+0,3 (изменение параметра цикла)

5. Проверить на окончание цикла. Если X<=0,7, перейти к п.2, иначе окончание счета

Блоки 2,3 - тело цикла образуют линейный участок вычислительного процесса. Параметр X - простая переменная вещественного типа.

Для Х известно начальное ( 0.1 ), конечное ( 0.7 )значения и шаг изменения ( 0.3 ).

Выход из цикла произойдет при X>0.7 ( 1 )

Эту задачу называют еще задачей табулирования функции на заданном диапазоне изменения аргумента. В инженерных расчетах такая задача встречается, когда необходимо получить таблицу значений некоторой величины, определяемой формулой, если известно, что один из параметров, входящих в эту формулу, может принимать любые значения в диапазоне [a;b].

Шаг h изменения параметра выбирается в зависимости от того, сколько значений табулируемой величины нужно получить.

Графическая блок-схема алгоритма будет такой:

Ввод

Х=0,1

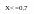
да

нет

Действия над массивами

Как правило, в задачах необходимо обрабатывать массивы - последовательности чисел разных размеров и типов. В этом случае используется доступ к каждому элементу описанного массива по его номеру (индексу), определяющему местоположение конкретного элемента в массиве. Это можно сделать, указав идентификатор ( имя ) массива и индекс элемента в квадратных скобках.

< Пример >:

Массив А[1..15] вещественный (это значит, что массив А-последовательность вещественных

чисел)

. . .

А[1]:=1,3; А[2]:=2,1; А[3]:= -1,5 . . . – элементы массива А

< Пример >:

Массив А [1..10] целый; (это значит, что массив А - последовательность из 10 целых чисел)

. . .

А[1]:=1; А[2]:=2; А[3]:=А[1]+А[2]; . . .(элементы массива А)

Понятно, что при работе с двумерным массивом указываются два индекса.

< Пример >:

массив А [1..10,1..5] целый; (матрица из 10 строк и 5 столбцов)

. . .

А[1,1]:=1; (Элемент равен 1, стоит в 1 строке, 1 столбце матрицы)

А[2,1]:=4; (Элемент равен 4, стоит во 2 строке, 1 столбце матрицы)

А[1,2]:=А[1,1]+А[2,1]; (Элемент равен 1+4=5, стоит в 1 строке, 2 столбце матрицы)

Индексированные элементы массивов могут использоваться, как простые переменные соответствующего типа: использоваться в условных и циклических конструкциях, входить в качестве параметров операторов ввода/вывода, им можно присваивать любые значения, соответствующие их типу.

ПОИСК ЭЛЕМЕНТОВ - реализуется сочетанием операторов цикла и условных, задающих условие поиска. Иногда вводятся дополнительные переменные для подсчета или суммирования нужных элементов или их значений. В некоторых задачах такие дополнительные переменные могут понадобиться для запоминания местоположения нужных элементов, т.е. значений их индексов.

Рассмотрим пример 7.

Найти сумму отрицательных элементов массива А=A₁;A₂;A₃…A_N и их местоположение.. (здесь 1,2,3,… - индексы, указывающие местоположение элемента в массиве А. N – количество элементов в массиве)

Нам нужна дополнительная переменная, в которой будем накапливать сумму отрицательных элементов массива – назовем ее S. Еще нужна переменная – назовем ее В - это будет массив, состоящий из порядковых номеров отрицательных элементов массива А. Количество элементов в массиве В считаем с помощью переменной J. Просмотром элементов массива А управляет переменная I.

Рассмотрим пример на произвольном массиве А=2; -3,4; 1; 2; -2; 1,5; 4,4; -3; 10,8; 6, т.е. 10 произвольных чисел (N=10). Если массив будет состоять из 100 или 1000 чисел, алгоритм решения будет такой же, как и для 10 чисел, поэтому для простоты и визуального просмотра исходного массива мы ограничимся 10 элементами массива.

Для ввода и вывода произвольной последовательности чисел необходимо организовывать цикл.

Запишем словесный алгоритм примера 7.

1. Присвоим переменной I начальное значение, т.е. I = 1

2. Ввести очередной элемент массива А, т.е. А[I], (для нашего массива A[1]=2)

3. Проверить все ли элементы массива А введены, т.е. I <N. Если “да”, то перейти к пункту 4, иначе перейти к пункту 5.

4. Увеличить значение переменной I, т.е. I=I+1. Перейти к пункту 2. (В пунктах 1- 4 мы записали алгоритм (цикл) поэлементного ввода нашего массива А). Теперь с помощью индекса I, опять же поэлементно, начнем просматривать наш массив.

5. Присвоим начальные значения переменным S и J, т.е. S=0; J=0 (мы еще ничего не вычисляли, содержимое переменных пусто. Вспомним, что в этих переменных должны в конце решения получить!)

6. Присвоим I=1 (организуем цикл проверки на отрицательность, начиная с первого элемента массива А)

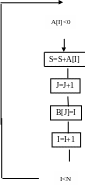
7. Проверить А[I]<0?. Если “нет”, то переходим к пункту 9. Если “да”, то переход к пункту 8

8. Прибавляем этот элемент к значению переменной S, а индекс I элемента A[I] занесем в массив В, предварительно увеличив индекс J, т.е. S=S+A[I]; J=J+1; B[J] = I. (Все эти действия в блок-схеме можно записать в одном блоке)

9. Увеличить значение переменной I, т.е. I=I+1. (Подготовка просмотра следующего элемента массива А)

10. Проверить все ли элементы массива А просмотрели на отрицательность, т.е. если I <=N. то перейти к пункту 7, иначе перейти к пункту 11.

11. Вывести на печать значение переменных S, J.(В нашем примере S= -3,4+(-2)+(-3)= -8,4; J=3, т.к. количество отрицательных элементов в массиве равно 3)

Вывести массив В. В нашем примере он будет состоять из элементов 2;5;8, т.к. на 2-м, 5-м, 8-м местах стоят отрицательные элементы в массиве А. Значение переменной J будет равно 3.

Так как В - массив, то для его вывода организуем цикл аналогичный вводу нашего массива A, для этого можно вновь использовать переменную I, т.к. с массивом А работа закончена,

12. т.е. присвоим I=1

13. Вывести на печать В[I]

14. Проверить все ли элементы массива В просмотрены, т.е. если I<J, то перейти к пункту 14, иначе к пункту 16

15. Увеличить значение переменной I, т.е. I=I+1. Перейти к пункту 13

16. Закончить счет.

Графический алгоритм примера 7.

I=1

N=10

Цикл ввода элементов массива А

да

I=I+1

нет

S=0

J=0

I=1

нет

Цикл проверки элементов массива А на знак, вычисление суммы (S) отрицательных элементов массива А, формирование массива В из порядковых номеров отрицательных элементов в массиве А

да

да

нет

Вывод S,J

I=1

Цикл вывода элементов массива В

Вывод В[i]

да

I=I+1

нет

Конец

счета

Рассмотрим Пример 8

В произвольном массиве найти максимальный и минимальный элементы и поменять их местами.

Возьмем тот же массив из примера 7.

А=2; -3,4; 1; 2; -2; 1,5; 4,4; -3; 10,8; 6

Переменную под максимальный элемент назовем Мax, его местоположение в массиве запишем в переменную Nmax, переменную под минимальный элемент назовем Min, его местоположение в массиве запишем в переменную Nmin. (наименование этих переменных совершенно произвольно, мы такие берем для наглядности).

На процедуре ввода останавливаться не будем, это подробно рассмотрели в примере 7.

(перейдя к пункту 1, мы перейдём к поиску максимума нашего массива и найдём на каком месте он стоит в нашем массиве)

1. Мах=A[1], Nmax=1 (этими действиями мы присвоили переменной Max значение первого элемента из нашего массива равного 2, а переменной Nmax значение равное 1, т.е. значение места, на котором он стоит. Так оно и будет, если бы на первом месте в массиве стояло самое большое число).

2. I=2 (переменной I присвоим значение 2, таким образом мы подготовимся к просмотру элемента массива, стоящего на втором месте).

3. Если A[I] > Max, то переходим к пункту 4, иначе п.5

4. Max=A[I], а Nmax=I, (т.е. если очередной элемент оказался больше содержимого переменной Max, то значение этого элемента записываем в Max, а значение индекса I, указывающего на каком месте стоит этот элемент в переменную Nmax и после этого переходим к п.5. Если A[I] окажется меньше содержимого Max, то сразу переходим к подготовке просмотра следующего элемента массива – пункт 5)

5. Увеличим значение переменной I, т.е. I=I+1 (подготовим следующий элемент)

6. Все ли элементы массива А проверены?, т.е. если I < =N, то перейти к пункту 3, иначе перейти к пункту 7. ( с пункта 7 начнем поиск минимального элемента аналогично поиску максимального)

7. Мin=A[1], Nmin=1 (этими действиями мы присвоили переменной Min значение первого элемента из нашего массива равного 2, а переменной Nmin значение равное 1, т.е. значение места, на котором он стоит).

8. I=2 (переменной I присвоим значение 2, таким образом мы подготовимся к просмотру элемента массива, стоящего на втором месте).

9. Если A[I] < Min, то пункт 10, иначе п.11

10. Min=A[I], а Nmin=I (т.е. если очередной элемент оказался меньше содержимого переменной Min, то значение этого элемента записываем в Min, а значение индекса I, указывающего на каком месте стоит этот элемент в переменную Nmin и после этого переходим к п.11. Если A[I] окажется больше содержимого Min, то сразу переходим к пункту 11, т.е. подготовке просмотра следующего элемента массива)

11. Увеличим значение переменной I, т.е. I=I+1 (подготовим следующий элемент)

12. Все ли элементы массива А проверены?, т.е. если I < =N, то перейти к пункту 9, иначе перейти к пункту 13.

Мы нашли максимальный и минимальный элементы, нашли их местоположение в нашем массиве. Теперь в пункте 13 надо поменять местами элемент массива A[Nmax] с элементом A[Nmin]. Это задача о двух стаканах. Если у нас 2 стакана с разным содержимым и нам надо поменять содержимое, то придется взять третий стакан. Для роли третьего стакана возьмем переменную V.

13. V= A[Nmax]; A[Nmax]= A[Nmin]; A[Nmin]= A[Nmin]=V (Поменяли местами максимум и минимум).

14. Вывести на печать значение переменных Max, Nmax, Min, Nmin (В нашем примере Max=10,8; Nmax=9; Min= -3,4; Nmin=2)

Еще нам надо организовать цикл на вывод массива A, т.к. мы его видоизменили (меняли местами два элемента. На выходе будет массив А=2; 10,8; 1; 2; -2; 1,5; 4,4; -3,4; -3; 6 ).

13. Присвоим I=1

14. Вывести на печать А[I]

15. Проверить все ли элементы массива А просмотрены, т.е. если I<N, то перейти к пункту 18, иначе к пункту 19

16. Увеличить значение переменной I, т.е. I=I+1. Перейти к пункту 16

17. Окончание счета

Графический алгоритм примера 8.

I=1

N=10

I=I+1

Цикл ввода элементов массива A

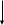
I<N

да

нет

Мах=A[1], Nmax=1

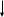
I=2

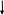
Нахождение максимального элемента и его местоположения в массиве

нет

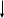
да

Max=A[I]

Nmax=I

I=I+1

да

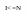
нет

Мin=A[1], Nmin=1

I=2

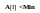
нет

да

Min=A[I]

Nmin=I

Цикл поиска минимального элемента и его местонахождения в массиве

I=I+1

да

нет

V=A[Nmax]

A[Nmax]=A[Nmin]

A[Nmin]=V

Вывод Max, Nmax, Вывод Min, Nmin

I=1

Вывод A[I]

Цикл вывода элементов массива A

I=I+1

да

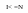
нет

Конец счета