7.2. Однофакторный дисперсионный анализ

Т-тест позволяет сопоставить только две градации. Проанализировать средние значения всех переменных можно с помощью метода однофакторного дисперсионного анализа One-Way ANOVA. Задача может быть сформулирована следующим образом: оказывает ли значимое влияние на значение некоторой количественной переменной интересующая нас переменная, которая измерена на номинальном или порядковом уровне?

Та переменная, которая должна оказывать влияние на конечный результат называется фактором. Например, в модели, объясняющей различия в готовности респондентов голосовать на выборах их возрастом, переменная «Собираетесь ли вы голосовать на выборах» будет выступать фактором. Конкретное значение фактора (например, готовность голосовать) называют уровнем фактора. Значение измеряемого признака (в нашем случае – возраст) называют откликом.

•  Выберите в подменю команду One-Way ANOVA... (Однофакторный дисперсионный анализ)

Подобная возможность есть и в первом пункте подменю (Means...), но она дает значительно более ограниченные возможности для анализа, и поэтому мы ее не рассматриваем. Появится диалоговое окно One-Way AN OVA.

•  Перенесите переменную «возраст» в список зависимых переменных (Dependent List), a переменную «собираетесь ли вы голосовать на выборах» — в поле Factor (Фактор).

•  Посмотрите, какие параметры можно задать для этого теста (кнопка Options...). Задайте вывод описательной статистики (флажок Descriptive) и проверку на гомогенность дисперсий (флажок Homogeneity-of-variance).

• С помощью флажка Means plot (График средних) можно построить диаграмму, на которой будут изображены средние значения для каждой выборки.

•  Запустите тест, щелкнув на ОК.

Выведенные результаты будут содержать:

•  результаты теста Ливина на гомогенность дисперсий,

•  типовую схему дисперсионного анализа, включая вероятность ошибки р (значимость) для оценки общей значимости,

• график средних.

У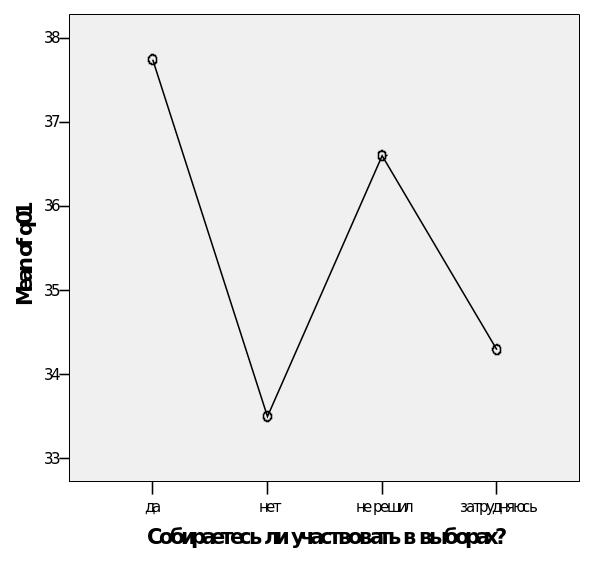 становка флажка Descriptives показывает: количество наблюдений, средние значения, стандартные отклонения и стандартные ошибки средних, 95 % доверительные интервалы, минимумы и максимумы для всех слоев фактора.

Критерий однородности дисперсий (Test of Homogeneity of Variances) позволяет вывести информацию о степени пригодности данных к дисперсионному анализу. Значимость критерия однородности дисперсии Ливина – 0,370 (больше 0,05) показывает, что дисперсии для каждой из групп статистически достоверно не различаются. Следовательно, результаты ANOVA могут быть признаны корректными.

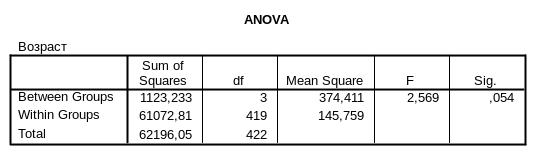
Таблица однофакторного дисперсионного анализа. Самым важным в этой таблице является уровень значимости Sig. р= 0,054. Он показывает, что разность между средними значениями переменной «готовность голосовать» для разных возрастов статистически незначительна.

Задание.

1. По массиву данных файла opros.sav найти средние значения доходов респондентов в месяц. С помощью t-теста для независимых выборок провести анализ различий средних значений доходов от места жительства респондентов.

2. По массиву данных файла opros.sav выяснить насколько доход в месяц (var42) различен для респондентов с разным уровнем образования (var60). Провести однофакторный дисперсионный анализ. Проанализировать полученные результаты.