7. Анализ взаимосвязей качественных и количественных переменных. Средние значения
Достаточно распространенная задача – демонстрация средних значений каких-то количественных показателей в социальных, демографических или каких-то иных группах. Например, необходимо сопоставить величину средней заработной платы в группах респондентов, опрошенных в разных типах населенных пунктов, либо сравнить средний возраст людей, проголосовавших за разных кандидатов на выборах, и т.п.
Построение статистических таблиц в рамках пакета программ SPSS выполняется с помощью команды Means (Средние) в рамках блока команд Compare Means.
В главном меню команды Means видно, что необходимо задать два типа переменных. Первый тип переменных – Dependent List (зависимые переменные) – это переменные, средние значения которых необходимо вычислять. Например, переменная «доход в месяц». Второй тип переменных - Independent List (независимые переменные) – это те переменные, которые определяют разделение всей совокупности опрошенных на определенные группы. Например, переменная «место жительства». Самый большой в среднем доход демонстрируют респонденты г. Сургута – около 17 тыс. рублей в месяц, самый низкий – опрошенные из Березовского района (8 тыс. рублей).
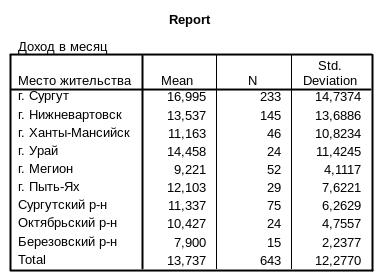
Исходя из данных таблицы, мы можем визуально убедиться в наличии различий в средних доходах респондентов, проживающих в разных территориях ХМАО. Но, например, различия в средних возрастах респондентов разных территорий визуально могут быть неочевидны. Для этого требуются математические доказательства.
Наличие либо отсутствие различий средних значений можно вычислить с помощью команды Т-test и One-Way ANOVA (дисперсионный анализ).
Команда Т-test (тест Стьюдента) решает задачу доказательства наличия различий средних значений количественной переменной в усеченном виде, а именно в случае, когда имеются лишь две сравниваемые группы.
7.1. Команда т-test (тест Стьюдента) для сравнения двух независимых выборок
Пример независимых выборок – разные населенные пункты, пол респондента.
Нужно выбрать в подменю команду Independent-Samples T Test... (t-тест для независимых выборок). Откроется диалоговое окно Independent-Samples T Test.
В списке исходных переменных щелкнуть на переменной «доход» и щелчком на кнопке с треугольником перенести ее в список тестируемых переменных (Test Variable(s)).
Таким же способом перенести переменную «место жительства» -terr- в поле Grouping Variable (Группирующая переменная).
Щелчком на кнопке Define Groups... (Определить группы) открывается окно, в котором можно ввести значения двух категорий для группирующей переменной «место жительства». Мы будем сравнивать две группы, удовлетворяющие условиям соответственно terr = 1 и terr = 9. Поэтому внесите в поле Group 1 (Группа 1) значение 1, а в поле Group2 — значение 9.
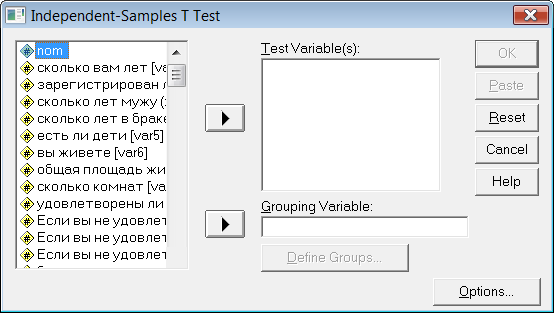Щелчком
на кнопке Continue вернутся в основное
диалоговое окно.
Теперь следует выяснить, какие параметры установлены по умолчанию. Щелкнуть для этого на кнопке Options... (Параметры). Не изменяя настроек, щелкнуть на кнопке Continue и вернутся в основное диалоговое окно. Запустить t-тест, щелкнув на ОК. В окне просмотра появятся следующие результаты:
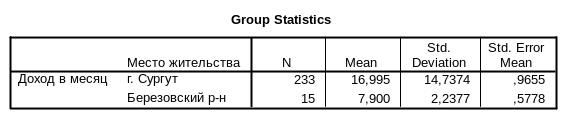
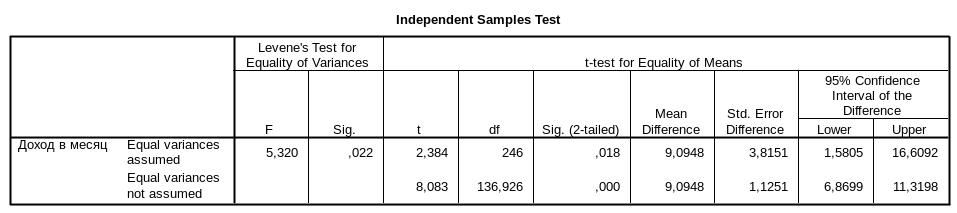
Первая часть таблицы – статистический тест Ливина (Levene’s Test for Equality of Variances) – тест проверки равенства дисперсий. F-статистика этого теста равна 5,320, а значимость этой статистики Sig. – 0,022. Значимость меньше 0,05. Дисперсии двух распределений статистически значимо различаются. Вторая часть таблицы (t-test for Equality of Means) – проверка равенства средних. Включает две строки – Equal variances assumed - соответствует равным дисперсиям и Equal variances not assumed – соответствует различным дисперсиям.
Полученные результаты говорят о различиях в средних доходах по двум территориям – г. Сургут и Березовский район. Различия статистически достоверны на высоком уровне значимости (р=0,000).