Критерий хи-квадрат по Пирсону

О бычно для вычисления критерия хи-квадрат используется формула Пирсона:

Здесь вычисляется сумма квадратов стандартизованных остатков по всем полям таблицы сопряженности. Поэтому поля с более высоким стандартизованным остатком вносят более весомый вклад в численное значение критерия хи-квадрат и, следовательно, — в значимый результат. Стандартизованный остаток (Std. Residual) 2 или более указывает на значимое расхождение между наблюдаемой и ожидаемой частотами.

В рассматриваемом нами примере формула Пирсона дает максимально значимую величину критерия хи-квадрат (р<0,001). Если рассмотреть стандартизованные остатки в отдельных полях таблицы сопряженности, то на основе вышеприведенного правила можно сделать вывод, что эта значимость в основном определяется полями, в которых переменная «готовность голосовать» имеет значение "нет". У молодых людей до 30 лет это значение повышено (2,2).

Корректность проведения теста хи-квадрат определяется двумя условиями: во-первых, ожидаемые частоты < 5 должны встречаться не более чем в 20% полей таблицы; во-вторых, суммы по строкам и столбцам всегда должны быть больше нуля.

В рассматриваемом примере это условие выполняется полностью. Как указывает примечание после таблицы теста хи-квадрат, только 12,5% полей имеют ожидаемую частоту менее 5.

Критерий хи-квадрат с поправкой на правдоподобие

Альтернативой формуле Пирсона для вычисления критерия хи-квадрат является поправка на правдоподобие. При большом объеме выборки формула Пирсона и подправленная формула дают очень близкие результаты. В нашем примере критерий хи-квадрат с поправкой на правдоподобие составляет 26,133.

Тест «линейно-линейная связь» (Linear-by-Linear Association)

Дополнительно в таблице сопряженности под обозначением linear-by-linear ("линейный-по-линейному") выводится значение теста Мантеля-Хэнзеля (3,826). Эта еще одна мера линейной зависимости между строками и столбцами таблицы сопряженности. Она определяется как произведение коэффициента корреляции Пирсона на количество наблюдений, уменьшенное на единицу:

Полученный таким образом критерий имеет одну степень свободы. Метод Мантеля-Хэнзеля используется всегда, когда в диалоговом окне Crosstabs: Statistics установлен флажок Chi-square. Однако для данных, относящихся к номинальной шкале, этот критерий неприменим.

Таблицы сопряженности, пример которых мы рассмотрели выше, имеют тот недостаток, что в них приводятся только абсолютные значения. Чтобы узнать, насколько эти значения важны по отношению к общему количеству, надо определить их процентную долю, для вычисления процентных значений нужно выполнить следующие действия:

•  выбрать в меню команды Analyze (Анализ) Descriptive Statistics (Дескриптивные статистики) Crosstabs... (Таблицы сопряженности)

•  Не изменяя прежних настроек, щелкнуть на кнопке Cells... Откроется диалоговое окно Crosstabs: Cell Display (Таблицы сопряженности: Отображение ячеек). В группе Percentages (Проценты) можно выбрать один или более из нижеследующих вариантов отображения:

•  Row (По строкам): Вычисляются процентные значения по строкам: количество наблюдений в каждой ячейке, отнесенное к сумме по строке.

•  Column (По столбцам): Вычисляются процентные значения по столбцам: количество наблюдений в каждой ячейке в отношении к сумме столбца.

•  Total (Полные): Вычисляются полные процентные значения: количество наблюдений в каждой ячейке, отнесенное к общей сумме наблюдений.

Таким образом, можно получить данные в двумерной таблице по строкам и столбцам и интерпретировать их в зависимости от заданной задачи. Возможно создание общей таблицы, где представлены проценты по строкам и колонкам таблицы, а так же частоты.

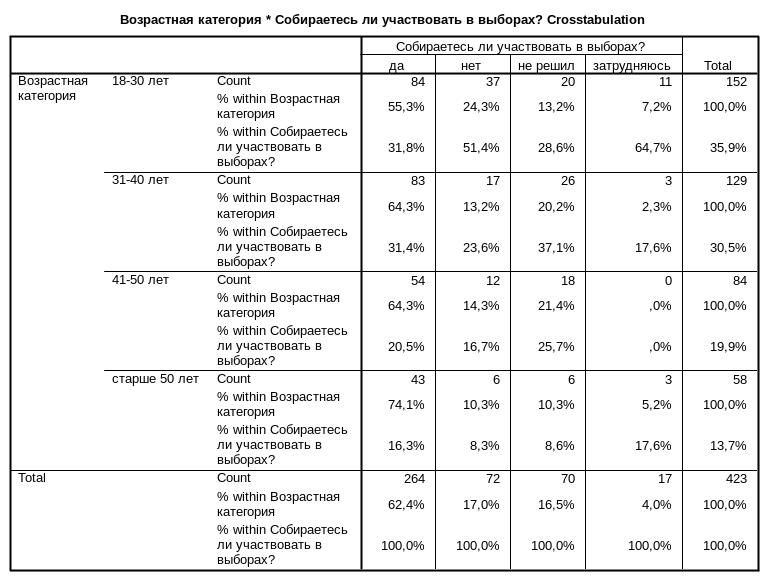
По данным таблицы можно сказать, что среди молодых респондентов в возрасте до 30 лет готовность прийти на выборы гораздо ниже, чем у респондентов других возрастных категорий. Только 55,3% молодых респондентов готовы придти и проголосовать на выборах. В категории респондентов старше 50 лет тех, кто придет голосовать значительно больше – 74,1%.

С другой стороны, из числа тех, кто не собирается голосовать на выборах, большинство составляют молодые респонденты – 51,4%, в возрасте от 45 до 50 лет таких респондентов в три раза меньше – 16,7%, среди пожилых – всего 8,3%. В категории тех, кто еще не решил голосовать ли ему не выборах, больше всего респондентов в возрасте от 31 до 40 лет – 37,1%.

Задание. 1. (по массиву данных файла opros.sav). Построить таблицу сопряженности двух переменных «Как вы относитесь к политической деятельности» и «vozrast» (с использованием интервальной шкалы). Проанализировать процентные соотношения.

2. Провести тест хи-квадрат переменных «Как вы относитесь к политической деятельности» и переменной «vozrast», выявить корреляционную зависимость/независимость этих переменных, по стандартизированному остатку, критерию хи-квадрата проанализировать связи переменных.

3. Исходя из задач и гипотез собственного исследования, выбрать переменные, удовлетворяющие условиям зависимости. Определить зависимые и независимые переменные. Построить таблицы сопряженности переменных собственного исследования, проанализировать данные на наличие зависимости переменных. Выяснить интенсивность зависимости переменных с помощью теста хи-квадрат.