Московский государственный технический университет
им. Н.Э. Баумана
Калужский филиал
Кафедра К5 - КФ
МЕТОД СЕЧЕНИЙ ПРИ РАСТЯЖЕНИИ, СЖАТИИ И КРУЧЕНИИ
(Методические указания по технической механике
Составитель: Борискин О.Ф.
Калуга 2002
1 . Расчет статически определимых стержней на растяжение и сжатие
1.Задача:
Для стального
ступенчатого стержня (А
и 2А
площади ступеней) длиной 4l,
на- груженного системой сил N,
нормальных напряжений
и осевых перемещений
W.
Решение:
1.1.Определим опорную реакцию.
Введем прямоугольную систему координат с центром О в жесткой заделке и направим ось Z вправо. Запишем уравнение равновесия для всего стержня:
1.2.Распределение нормальных сил.
Используя метод сечений, рассмотрим последовательно все четыре участка стержня.
1.2.1.Рассечем
брус на участке ВС,
отбросим его правую часть и рассмотрим
равновесие левой части бруса, нагруженной
на конце силой 2ql
и внутренней силой
(рис.
2б). Направим силу внутреннего взаимодействия
(
)
вдоль оси Z.
Запишем
уравнение равновесия для данной части
бруса:
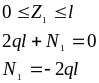
На эпюре нормальных сил (рис. 2е) отложим от нулевой линии вниз координаты, равные в некотором масштабе ql.
1.2.2.Проведем сечение на участке CD (рис. 2в), отбросим правую часть бруса и приложим к отсеченной части внешние и внутренние силы. Запишем условие равновесия:
1.2.3.На
участке DE
проведем сечение
и отбросим правую часть. Этот участок
нагружен равномерно распределенными
внешними силами, поэтому внутренняя
сила в сечениях этого участка зависит
от положения сечения (рис. 2г)
.
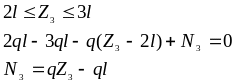
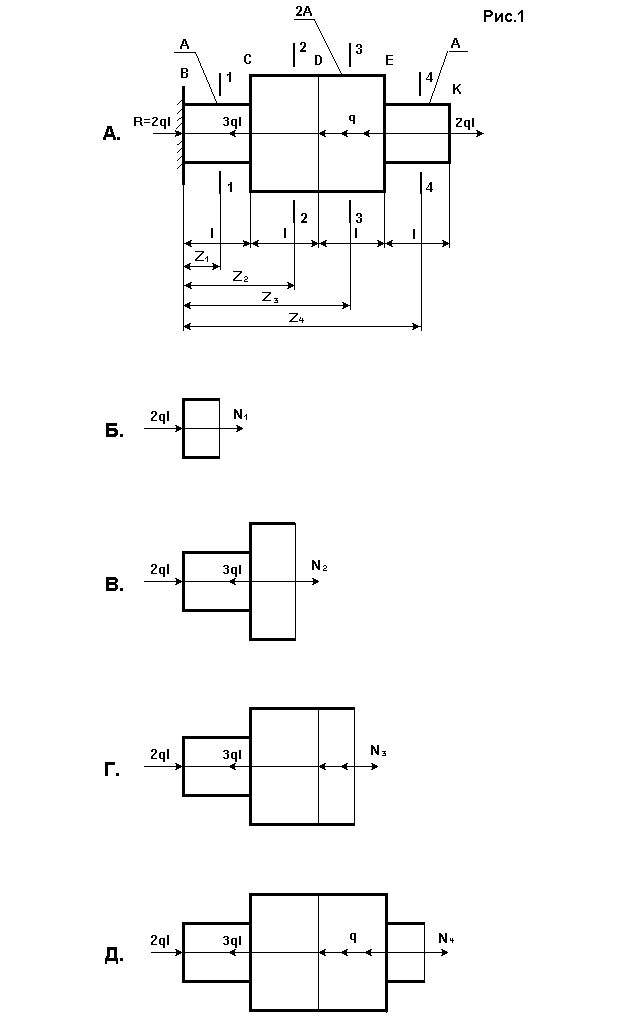
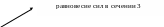
Рис. 2
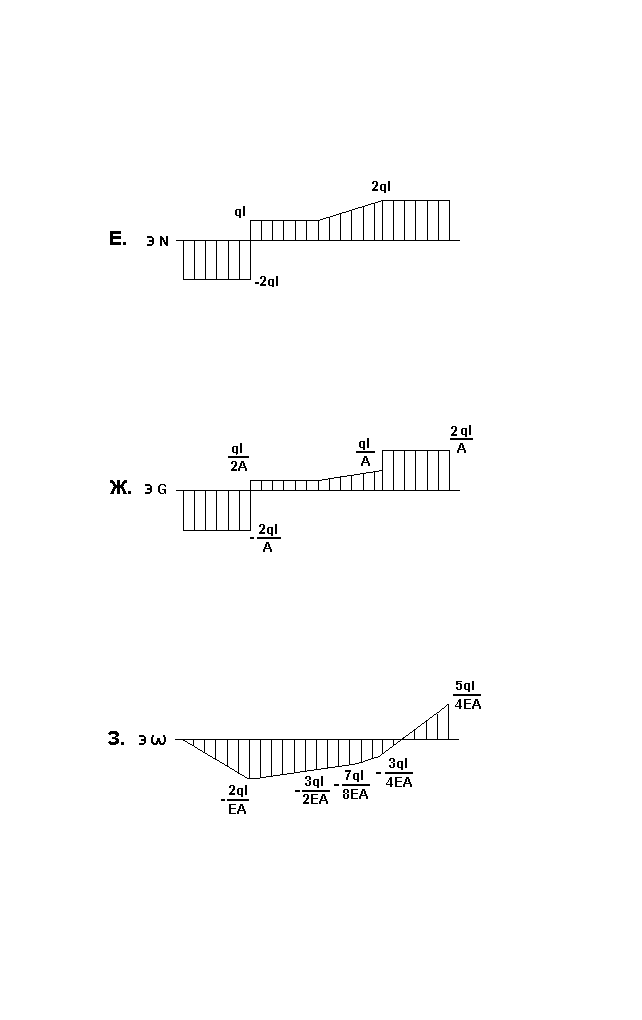
Рис. 2 (продолжение)
Найдем значения
на границах интервала:
Аналогично на
участке ЕК
построим сечение
(рис.
2д):
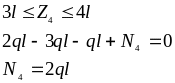
Окончательная эпюра нормальных сил приведена на рис. 2е.
1.3.Определение нормальных напряжений.
Для нахождения нормальных напряжений воспользуемся формулой:
(1.1)
Где N - нормальная сила в данном сечении;
А - площадь этого сечения.
Знак напряжения
определяется знаком нормальной силы
на рассматриваемом участке. Подставив
в формулу значения
и значения соответствующих площадей
сечений (А),
получим:
Для
имеем:
Подставив значения
на границах интервала, получим:
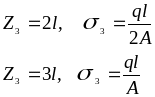
Окончательная эпюра нормальных напряжений представлена на рис. 2ж.
1.4.Определение осевых перемещений.
При определении продольных перемещений W при отсутствии температурных деформаций используется формула:
(1.2)
Из которой с учетом
закона Гука:
и формулы:
следует:
(1.3)
Где W - перемещение текущего значения Z по длине стержня;
N - нормальная сила в этом сечении;
EA - жесткость конструкции.
В качестве начала
отсчета примем закрепленную точку О
(начало
координат) (
).
Интегрируя формулу (1.2),
получим:
(1.4)
Где
-
удлинение рассматриваемого участка;
-
длина рассматриваемого участка.
Подставляя значения для N, l, и А, получим:
Определим результирующие перемещения (W) на границах участков как алгебраическую сумму удлинений участков, расположенных слева от рассматриваемой границы:
Окончательная эпюра перемещений представлена на рис. 2з.
1.5.Заключения по разделу.
Максимальные нормальные напряжения имеют место на участках ВС и ЕК и равны
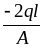и
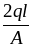соответственно.Максимальное перемещение наблюдается на участке ВС и равно
.
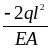