6.6.3. Ортонормированный базис

Для представления одномерных величин достаточно одного параметра. Например, при измерении длины используют один стандарт величины (сантиметры, миллиметры). Если принять, что 1 см – единица измерения, то 5 см больше 1 см в 5 раз, следовательно, выражается как 5 единиц. Так же и в векторном пространстве принято выбирать единицу измерения, которая выражает стандарт величины. Однако в двумерном пространстве одного параметра, измеряющего величину, недостаточно. Необходимы два параметра.

Пара взаимно перпендикулярных векторов 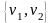называется ортогональным базисом. Кроме того, если 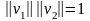, то эта пара называется ортонормированным базисом. Вектор с нормой, равной 1, называется единичным вектором. Иначе говоря, единичный вектор – это вектор, выражающий величину одной единицы измерения. Следовательно, ортонормированный базис представляет собой пару взаимно перпендикулярных единичных векторов, которые в совокупности с парой параметров дают величину вектора.

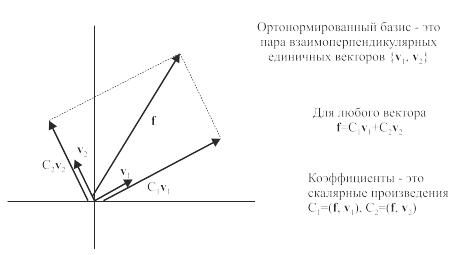
Рис. 6.21. Выражение вектора через ортонормированный базис

Выразим вектор f через векторы ортонормированного базиса 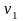, 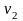и совокупность коэффициентов C₁, С₂ (рис. 6.21):

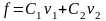. (6.6.8)

Коэффициенты (С₁, С₂) выражают величину составляющих вектора f в направлении и в направлении . Иначе говоря, определяют величину вектора. Любой вектор на плоскости можно выразить через это соотношение. Векторы 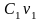и 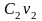называются проекциями вектора f.

Пусть дан вектор f и заранее образована система базисных векторов . Чтобы выразить вектор f через базис в соотношении (6.6.8), необходимо знать, как получить коэффициенты С₁ и С₂. Забегая вперед, представим коэффициенты С₁ и С₂ как скалярные произведения вектора f на каждый из векторов и :

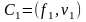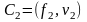, . (6.6.9)

ПРИМЕРЫ

Пример 1

Могут ли векторы и образовать базис, если

, .

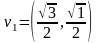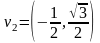Решение:

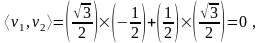
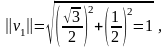
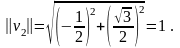
Следовательно, векторы и могут образовать базис.

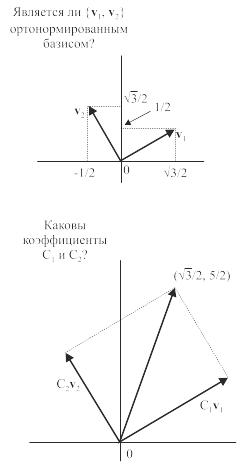
Пример 2

Разложить вектор

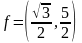
по базису , данному в примере 1.

Решение:

Вектор f можно представить как:

f = C₁v₁ + С₂ v₂/

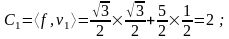
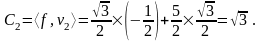
Следовательно,

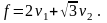
6.6.4. Переход от векторного пространства

к пространству функций

Выразим скалярное произведение и расстояние между векто­рами в многомерном пространстве. Рассмотрим, например, вектор трехмерного пространства:

.

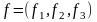Известно, что его норму или расстояние от исходной точки до точки 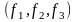можно выразить следующим образом:

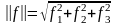_{. (6.6.10)}

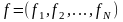Обобщая выражение (6.6.10), можно предположить, что норма вектора N-мерного пространства определяется следующим образом:

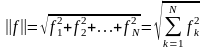_{. (6.6.11)}

А как же будет выглядеть норма вектора в случае пространства бесконечной размерности, иначе говоря, пространства функций. Норма функции f(t) (a < t <b) в этом случае является величиной функции. Каким же образом ее определить? Это становится понятным, если обратиться к формуле, которая и определится соотношением

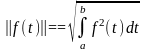
как обобщение векторной нормы. Чем больше интервал в этой формуле, тем больше значение нормы. Поэтому удобнее пронормировать норму функции f(t) относительно длины интервала:

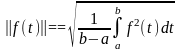_{. (6.6.12)}

По этой же причине в случае многовекторной нормы, чтобы избежать влияния размерности N, часто используют соотношение:

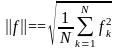_{. (6.6.13)}

Если сопоставить формулы нормы функции и нормы вектора, понятно следующее соответствие:

вектор функция сумма интеграл

Применяя это соответствие, можно осуществить естественное обобщение из векторного пространства в пространство функций.

Подводя итоги шестого раздела данной главы, отметим следующее.

1. Если для непрерывного сигнала 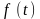произведена выборка из N его значений, то сигнал можно представить в виде N- мерного вектора, который задает одну точку в N-мерном пространстве.

2. Величина сигнала выражается нормой вектора, а отличие двух сигналов – расстоянием между векторами. Скалярное произведение определяется проекцией одного вектора на длину другого. Коэффициент корреляции выражает угол между векторами, а также степень похожести сигналов. Чем больше по абсолютной величине коэффициент корреляции, тем более похожи сигналы. Если он равен нулю, то векторы отображающие сигналы, взаимно перпендикулярны.

3. Множество взаимно перпендикулярных векторов, норма которых равна 1, называется ортонормированными базисами. Вектор можно разложить по базису, причем составляющие получаются с помощью скалярного произведения.

4. Функцию можно представить как одну точку векторного пространства с бесконечно большой размерностью (пространства функций). Так же, как и для векторов, можно определить норму функции, а для двух функций – расстояние, скалярное произведение и коэффициент корреляции.

КОНТРОЛЬНЫЕ ВОПРОСЫ И ПРАКТИЧЕСКИЕ ЗАДАНИЯ

1. Количество элементов черно-белого телевизионного изображения равно 512x512, число градаций по яркости – 256. Какой объем памяти необходим для хранения кадра такого изображения?

2. Дайте определение случайных и детерминированных сигналов.

3. С какой целью производится дискретизации аналогового сигнала?

4. Определите последовательность операций при переходе от аналогового сигнала к цифровому.

5. Какая система чисел образует двоичную систему счисления?

6. Проверьте равенство величин векторов 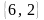и .

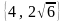7. Вычислите угол между векторами 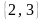и .

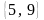8. Определите расстояние между векторами 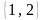и .

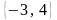9. Синусоидальный сигнал имеет период T =0,1 с. Каково значение частоты Найквиста для такого сигнала?

10. В чем заключается отличие между аналого-цифровым и цифро-аналоговым преобразованием?

11. Приведите примеры затухающих колебаний.

12. Почему уменьшается уровень шума в зашумленном сигнале при вычислении скользящего среднего?

13. Приведите примеры детерминированных сигналов, случайных сигналов.

14. Как следует понимать выражение: «Непрерывная функция есть некоторый вектор?» Какие дополнительные условия отсутствуют в данном вопросе?