
- •Оглавление
- •Список сокращений
- •Часть I
- •Часть II
- •Часть I
- •Твоя альма матер – поволжский
- •Государственный технологический
- •Университет
- •1. Система высшего технического образования
- •1.1. Высшее образование
- •1.2. Инженерное образование в России
- •1.3. Чем университет отличается от института
- •1.4. Многоступенчатое образование: бакалавриат, магистрат
- •2. Пгту как пример государственного технического университета на рубеже XX и XXI веков
- •2.1. История вуза
- •2.2. Университет сегодня
- •Факультеты (в скобках – год основания):
- •2.3. Структура Поволжского государственного
- •2.3.1. Образовательная структура
- •2.3.2. Структура управления университетом
- •41 Рис. 2.3. Управленческая структура пгту
- •43 Рис. 2.4. Структура управления университетом
- •3. Студент в учебном процессе [2, 3]
- •3.1. Студент на лекции
- •3.2. Студент на практических занятиях
- •3.3. Студент в учебной лаборатории
- •3.4. Студент учится самостоятельно
- •3.5. Студент на экзамене
- •3.6. Роль компьютера и Интернета в образовании
- •Часть II основы радиотехники и радиоэлектроники
- •1. История развития радиотехники
- •2. Принципы радиотехники [2, 3, 5]
- •2.1. Возникновение электромагнитного поля
- •2.2. Распространение электромагнитных полей. Радиоволны
- •2.3. Использование высокочастотных колебаний
- •2.4. Генерация колебаний синусоидального вида
- •Синусоидальной формы
- •2.5. Принципы приема радиосигналов
- •2.6. Борьба с помехами
- •3. Электрорадиоэлементы [13, 14]
- •3.1. Резистивные элементы электронной техники
- •3.1.1. Общие сведения о резисторах
- •3.1.2. Основные параметры резисторов
- •3.1.3. Резисторы постоянного сопротивления
- •3.1.4. Система обозначений и маркировка резисторов
- •3.1.5. Специальные резисторы
- •3.2. Емкостные элементы электронной техники
- •3.2.1. Общие сведения о конденсаторах
- •3.2.2. Классификация и конструкции конденсаторов
- •3.2.3. Параметры конденсаторов
- •3.2.4. Система обозначений и маркировка конденсаторов
- •3.2.5. Основные разновидности конденсаторов
- •3.3. Индуктивные элементы электронной техники
- •3.3.1. Физическая природа индуктивности
- •3.3.2. Конструкции катушек индуктивности
- •3.3.3. Разновидности катушек индуктивности
- •3.4. Трансформаторы
- •4. Полупроводниковые приборы
- •4.1. Полупроводниковые материалы
- •4.2. Электроны и дырки в полупроводниках
- •4.3. Примеси и дефекты
- •4.4. Электронно-дырочный переход (p-n типа)
- •4.5. Полупроводниковые триоды (транзисторы)
- •4.6. Полупроводниковые интегральные схемы
- •5. Прикладные программы для решения
- •5.1. Система схемотехнического моделирования
- •5.1.1. Общие сведения
- •5.1.2. Основные достоинства программы
- •5.1.3. Компоненты и проведение экспериментов
- •5.2. Среда программирования LabView
- •5.3. Пакет прикладных программ matlab
- •5.3.1. Общие сведения
- •5.3.2. Математика и вычисления
- •5.3.3. Наборы инструментов
- •5.4. Система компьютерной алгебры Mathcad
- •5.4.1. Основные сведения
- •5.4.2. Основные возможности
- •5.4.3. Интерфейс
- •5.4.4. Графика
- •5.4.5. Расширение функциональных возможностей
- •5.4.6. Сравнительная характеристика
- •5.4.7. Решение уравнений в MathCad
- •5.4.8. Решение систем уравнений в MathCad
- •5.4.9. Программирование в MathCad
- •189 Рис. 5.2. Пример решения систем уравнений
- •6. Элементы теории цифровой обработки сигналов
- •6.1. Когда необходима обработка сигналов
- •6.2. Виды сигналов
- •6.2.1. Случайные сигналы
- •6.2.2. Виды детерминированных сигналов
- •6.3. Аналоговые и цифровые сигналы
- •6.4. Проблема выборки
- •6.5. Примеры обработки сигналов
- •6.5.1. Сглаживание сигнала
- •6.5.2. Подавление шумов
- •6.6. Математические модели сигналов
- •6.6.1. Математическое представление сигнала
- •6.6.2. Скалярное произведение и расстояние для двумерных векторов
- •6.6.3. Ортонормированный базис
- •6.6.4. Переход от векторного пространства
- •7. Радиотехнические системы
- •7.1. Классификация ртс
- •Диапазоны радиочастот
- •7.2. Тактико-технические характеристики ртс
- •7.3. Радиолокационные системы
- •7.3.1. Задачи, решаемые радиолокационными системами
- •7.3.2. История радиолокации
- •7.3.3. Принципы построения радиолокационных систем
- •7.3.4. Классификация радиолокационных систем
- •7.4. Современные радиолокационные системы
- •7.4.1. Радиолокационные станции управления воздушным движением
- •7.4.2. Рлс обнаружения, наведения и целеуказания
- •7.4.3. Рлс обнаружения маловысотных целей
- •7.4.4. Рлс наведения зенитных управляемых ракет
- •7.4.5. Рлс и комплексы разведки на поле боя
- •7.4.6. Рлс подповерхностного зондирования
- •7.4.7. Рлс противоракетной обороны
- •7.4.8. Корабельные рлс
- •7.4.9. Авиационные (самолетные) рлс
- •7.5. Радионавигационные системы
- •7.5.1. Общие сведения и история развития
- •7.5.2. Спутниковые системы навигации
- •7.6. Ртс передачи информации
- •Заключение. О тенденциях в современной радиоэлектронике
- •Словарь радиоэлектронных терминов
- •Список литературы
- •Именной указатель
- •Предметно алфавитный указатель
- •424000 Йошкар-Ола, пл. Ленина, 3
- •424006 Йошкар-Ола, ул. Панфилова, 17
6.6.2. Скалярное произведение и расстояние для двумерных векторов
Сделав выборку некоторого сигнала f(t), возьмем из нее два значения f1 и f2. Таким же образом получим два значения для некоторого сигнала g(t) (рис. 6.17).
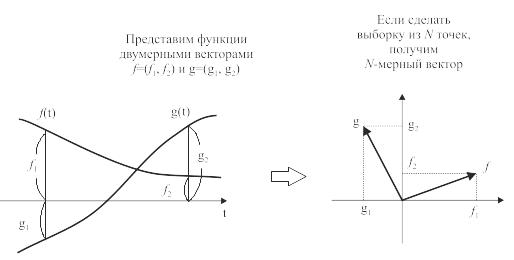
Рис. 6.17. Векторное выражение функции
Что же нужно сделать для того, чтобы узнать степень взаимоотношения между двумя сигналами f(t) и g(t), исходя из их значений? Если сделать выборку, состоящую всего лишь из двух значений, то, естественно, степень приближения к первоначальному сигналу невысока. Как показано выше, эта проблема разрешится, если увеличить число элементов выборки. Но пока рассмотрим случай выборки из двух точек.
Итак, определим векторы, содержащие по два элемента из выборки каждого сигнала, иначе говоря, двумерные векторы.
Обозначим их как f и g:
f = (f1, f2), g = (g1, g2).
Если сигналы выразить через векторы таким образом, то исследование отношений между ними есть исследование отношений между векторами. В чем же заключается такое исследование?
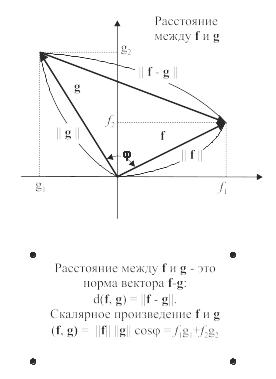
Рис. 6.18. Расстояние и скалярное произведение двумерных векторов
Во-первых, нужно выяснить, насколько удалены векторы f и g, т. е. измерить расстояние между векторами (рис. 6.18). Пусть d(f, g) – расстояние между векторами f u g. Чем меньше значение d, тем ближе векторы f и g, а значит, и сильнее между ними взаимосвязь.
Величину
вектора f
(абсолютное
значение) обозначим как
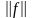 .
Используя
компоненты вектора f,
получим:
.
Используя
компоненты вектора f,
получим:
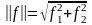 . (6.6.1)
. (6.6.1)
называют также нормой вектора f.
Итак, очевидно (см. рис 6.18), что расстояние между векторами f и g есть норма вектора f – g. Это можно записать, используя компоненты векторов, в следующем виде:
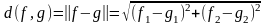 . (6.6.2)
. (6.6.2)
Расстояние – это один из параметров, измеряющий силу связи между векторами. Однако посмотрите на рис. 6.19. На этом рисунке векторы g и h одинаково удалены от вектора f. Но векторы g и f имеют одно направление, а вектор h расположен под углом к вектору f. Поэтому, увеличив вектор f в несколько раз, можно получить вектор g и невозможно получить вектор h. Несмотря на равноудаленность g и h от вектора f, связь f и g гораздо сильнее. Видимо, было бы недостаточно выражать связь между векторами одним лишь расстоянием. Необходимо также учитывать угол между ними (рис. 6.19).
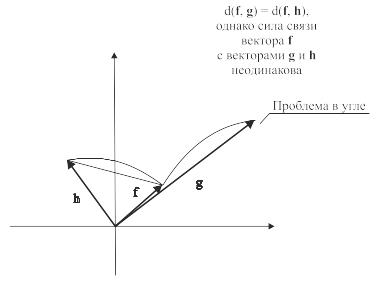
Рис. 6.19. Связь между векторами
Для выражения связи между векторами используют скалярное произведение. Скалярное произведение между f и g обозначается как (f, g) и определяется следующим образом:
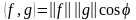 . (6.6.3)
. (6.6.3)
Следовательно,
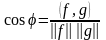 .
.
Обозначим эту величину
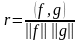 , (6.6.4)
, (6.6.4)
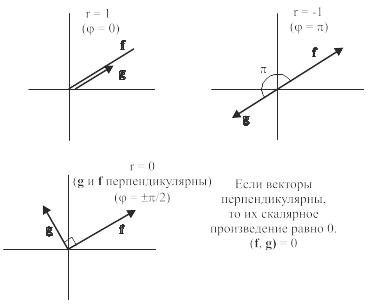
Рис. 6.20. Коэффициент корреляции
Величина
выражает
силу связи между векторами f
и g
через
угол между ними (рис.
6.20).
Если направления f
и
g
совпадают
(т. е.
= 0), то
принимает
максимальное значение, равное 1. С
увеличением угла
значение
уменьшается.
Если
=
0,
т. е.
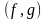 =
0, векторы
f
и g
взаимно
перпендикулярны. Назовем величину
коэффициентом корреляции. Как
видно из соотношения (6.6.4),
зависит от угла
между
векторами и не зависит от нормы векторов.
=
0, векторы
f
и g
взаимно
перпендикулярны. Назовем величину
коэффициентом корреляции. Как
видно из соотношения (6.6.4),
зависит от угла
между
векторами и не зависит от нормы векторов.
Как выразить скалярное произведение, используя компоненты вектора? Это можно сделать следующим образом.
Чтобы вывести эту формулу, применим теорему косинусов для векторов (см. рис. 6.18):
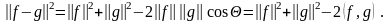
Следовательно,
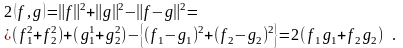 Скалярное
произведение вектора f
на
самого себя равно:
Скалярное
произведение вектора f
на
самого себя равно:
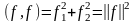 (6.6.6)
(6.6.6)
и выражает связь между скалярным произведением и нормой.
Подставим полученные результаты в выражение коэффициента корреляции (6.6.4) и представим следующим образом:
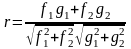 . (6.6.7)
. (6.6.7)
