6.6. Математические модели сигналов
6.6.1. Математическое представление сигнала
По своей природе сигнал отображает реальную физическую величину. Если представить его функцией или набором числовых значений, то возникает проблема обработки сигнала как функции или как набора числовых значений.
В разделе 6.1 было рассмотрено преобразование изменяющегося во времени аналогового сигнала f(t) при соответствующем интервале дискретизации и представлении выборок в цифровой форме. При малом интервале дискретизации можно достаточно точно воспроизвести первоначальный аналоговый сигнал по цифровому сигналу. Если временной интервал [а, б] разделить на одинаковые отрезки, а сигнал f, уже подвергшийся дискретизации, перевести в цифровую форму и записать в виде ряда значений N точек
f = (f1, f2, …,fN),
то f можно представить N-мерным вектором. N-мерным вектором называется величина, представленная набором числовых значений N, расположенных в определенном порядке. Элемент из этого числового набора называется компонентой вектора.
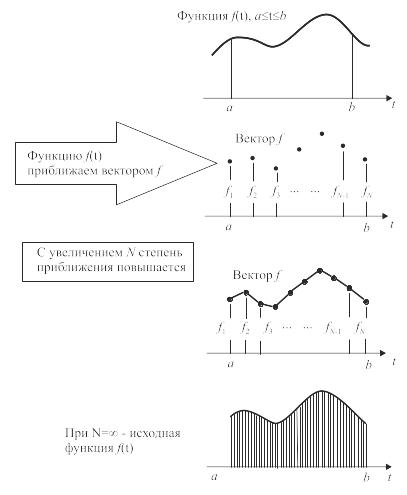
Рис. 6.15. Векторное представление функции
Качество приближения функции f(t) меняется в зависимости от числа N. Если N увеличивать, то степень приближения заметно улучшается. Если увеличивать N до бесконечно большого числа, то вся информация, содержащаяся в f(t), будет содержаться в f (рис. 6.15).
Это означает, что, в сущности, анализ вектора f вместо функции f(t) (если она не является «особой», т.е. не имеет точек разрыва) аналогичен анализу непрерывно изменяющегося во времени сигнала f(t).
Двумерный вектор, расположенный в двумерном пространстве (или, иначе говоря, на плоскости), соответствует какой-либо одной точке на этой плоскости (рис. 6.16).
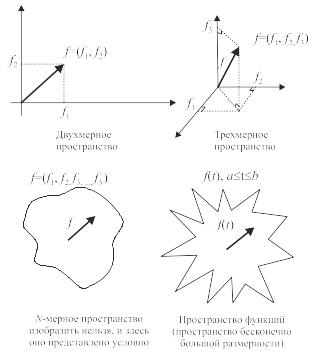
Рис. 6.16. Векторное пространство и пространство функций
Трехмерный вектор соответствует одной точке в трехмерном пространстве, а N-мерный вектор также соответствует одной точке, но N-мерного пространства (к сожалению, изобразить это мы не можем). Если представить пространство бесконечно большой размерности N, то можно предположить, что непрерывная функция f(t) соответствует одной точке этого пространства. Назовем это невидимое абстрактное пространство бесконечной размерности пространством функций.
Что касается вектора в двумерном пространстве или, иначе говоря, вектора на плоскости, то необходимо вспомнить, как выражаются угол и величина (длина) вектора через расстояние и скалярное произведение. Если представить сигнал, который мы собираемся обработать, в форме вектора, то, используя эти понятия, можно прояснить свойства сигнала.
При размерности векторного пространства N > 2 также можно определить расстояние между векторами и скалярное произведение. Более того, если рассуждать подобным образом, то же самое можно сделать и для пространства функций. Одним словом, давая определение расстоянию и скалярному произведению в пространстве функций, можно говорить о величине и угле между функциями. Далее мы будем использовать понятие взаимно перпендикулярных функций и представлять их в виде взаимно перпендикулярных векторов. В этом случае при внешней сложности формул станет понятно, что подход, состоящий в использовании векторного расстояния и скалярного произведения для пространства функций, очень прост. При обработке сигналов оперируют такими понятиями, как функция корреляции и анализ Фурье, а они как раз основаны на использовании свойств расстояния и скалярного произведения при переходе от векторного пространства к пространству функции.