6.5. Примеры обработки сигналов

6.5.1. Сглаживание сигнала

В этом разделе мы рассмотрим способы обработки сигналов на примере данных, полученных в результате эксперимента. Для приблизительной оценки вида сигнала необходимо сделать его «гладким», удалив незначительный шум, входящий в сигнал. Данный вид обработки называют сглаживанием сигнала.

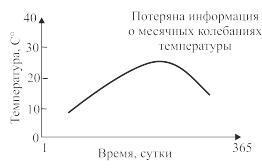
Например, на рассмотренных ранее температурных графиках мы видим довольно плавное изменение среднемесячной температуры в течение года (рис. 6.7). Для этого случая среднемесячная температура определялась следующим образом. Сначала вычислялась средняя температура первой половины месяца, затем средняя температура второй половины месяца, а средняя между этими двумя величинами бралась за основу. Но поскольку вследствие такой операции мы рассматриваем за год всего лишь 12 точек, то полученный график принял форму ломаной линии.

Если эту операцию провести относительно не только центральных точек (точек, соответствующих середине каждого месяца), но и относительно всех точек измерения, получим не ломаную, а гладкую кривую. Эта операция называется скользящим усреднением.

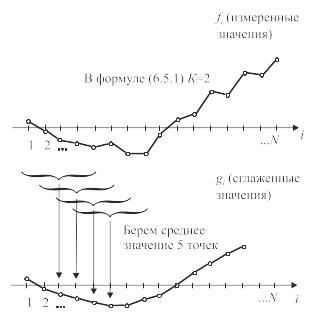
Иначе говоря, берем некоторую область до и после рассматриваемой точки и, учитывая численные значения измерений, входящих в эту область, вычисляем среднее значение (рис. 6.10).

Предположим, что дано N точек измерений цифрового сигнала {f₁, f₂,…,f_N}:

f_i; i = 1, 2, 3, …, N.

Рис. 6.10. Способ нахождения скользящего среднего

Для нахождения скользящего среднего в окрестности рассматриваемой точки i берем среднее арифметическое от К предыдущих и последующих точек, включая точку i. Одним словом, новые значения g_i для каких-либо точек i, представленные как средние значения этих 2К+1 точек, включающих точки i, определяем как значения сглаживания:

.

C использованием знака суммы это же соотношение записыва­ется в виде

. (6.5.1)

Обратим внимание на то, что на первых и на последних точках оси абсцисс невозможно вычислить значение сглаживания. Область, где это можно сделать, определяется следующим образом:

i = 1+ K, 2 + K,..., N-K.

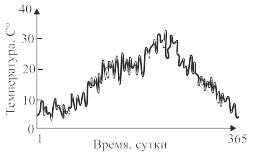
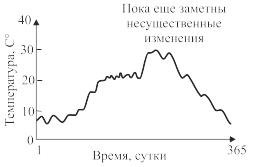
а) исходные данные	б) после скользящего усреднения при К=5
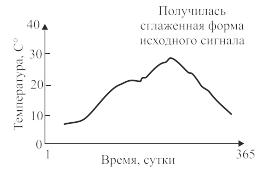
в) после скользящего усреднения при К=25	г) после скользящего усреднения при К=50
Рис. 6.11. Сглаживание графиков температуры атмосферы методом скользящего среднего

На рис. 6.11 представлен график средней температуры атмосферы, измеряемой каждый день в течение одного года. Попробуем сделать обработку методом скользящего среднего. Из графиков видно, что если число точек К, которые мы учитываем, достаточно большое, то форма сигнала сглаживается. Если число К слишком мало, то эффект сглаживания слабый, но если К слишком велико, то форма сигнала становится невыразительной. Как видно из этого факта, взять скользящее среднее – это все равно, что исключить из сигнала быстроколеблющуюся или, иначе говоря, высокочастотную его составляющую. Таким образом, область исключаемой частоты в зависимости от значения изменяется. Однако если мы возьмем область учитываемых точек только перед рассматриваемой точкой, а не до и после, то получим такой же эффект сглаживания. Это определяется соотношением

,

т.е.

. (6.5.2)

Все точки из интервала 2К+1, используемые при вычислении скользящего среднего, мы рассматриваем с одинаковой степенью значимости. Однако во многих случаях необходимо учитывать, что, чем ближе точка к рассматриваемой точке i, тем выше ее значимость, и соответственно с отдалением эта значимость уменьшается. Когда мы производим сглаживание, нужно определить вес каждой точки в соответствии с ее значимостью. Это можно записать следующим выражением:

. (6.5.3)

Чтобы не исказить величину усредняемой функции, примем следующее условие:

,

где – функция, дающая вес точкам. В качестве весовой функции обычно используется функция распределения Гаусса, представленная на рис. 6.12.

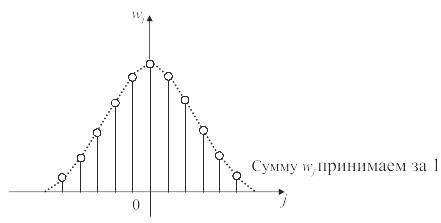
Рис. 6.12. Пример весовой функции (распределение Гаусса)