6.4. Проблема выборки

В процессе преобразования аналогового сигнала в цифровой очевидно, что чем шире интервал дискретизации выборки и грубее квантование, тем меньше требуется данных для представления сигнала. Однако если сигнал представлен слишком малым объемом данных, то возникает опасность потерять информацию, которую сигнал содержит.

Одна из основных проблем, с которой мы с самого начала сталкиваемся при обработке сигналов, – это проблема выбора интервала дискретизации выборки. Рассмотрим эту проблему на простом примере обработки данных температуры атмосферы.

а) почасовые измерения температуры

б) среднесуточная температура

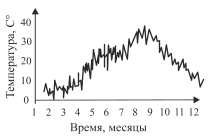
в) среднемесячная температура

Рис. 6.7. Выборка изменений температуры атмосферы

На рис. 6.7а представлен график температуры атмосферы в некотором выбранном месте в течение одного года с интервалом измерения в один час. Общее количество данных – 24 (измерений в день) х 365 (дней) = 8760 (измерений).

Если мы хотим знать, каким образом меняется температура в течение дня, то используем данные, снимаемые каждый час.

Если нужно проследить изменение температуры день за днем, то один из способов заключается в измерении температуры каждый день в определенное время. Но в этом случае возникает разница в результатах, зависящая от того, в какое время суток (днем или ночью) производятся измерения. Такой проблемы не возникает, если вычислять среднесуточную температуру.

На рис. 6.7б представлен результат такой обработки данных – график ежедневных значений средней температуры в течение года. А на рис. 6.7в изображен график изменения среднемесячной температуры атмосферы. Таким образом, в зависимости от временного периода меняется вид выборки. Одним словом, прежде чем производить выборку, нужно четко определить, какую информацию мы намерены получить от сигнала.

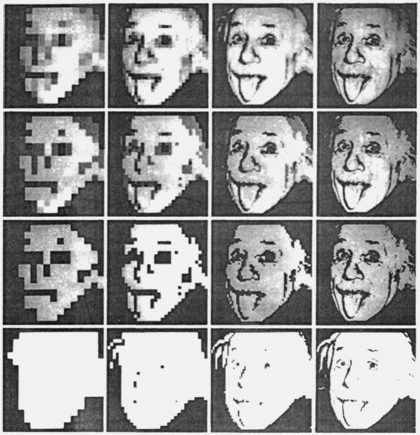
Рис.6.8. Телевизионное изображение для различного числа градаций и элементов изображения (фотография Эйнштейна после аналого-цифрового преобразования)

А что происходит в случае двумерного сигнала, например, в случае сигнала изображения? Оцифрованное изображение выражается множеством числовых точек, расположенных на пересечении линий вдоль осей абсцисс и ординат, подобно клеткам шахматной доски. Каждая в отдельности точка называется элементом телевизионного изображения, или пикселом. И чем этих пикселов больше, тем более четкое изображение можно получить (иначе говоря, повысить разрешающую способность). Число уровней квантования яркости называется градацией. Чем больше число градаций, тем лучше контрастность изображения.

На рис. 6.8 показано, как меняется изображение в зави­симости от числа градаций и элементов телевизионного изображения. Абсолютно ясно, что изображение в правом кадре имеет наиболее высокое качество и по яркости, и по контрасту.

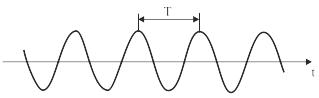
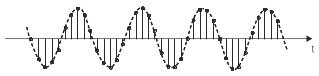
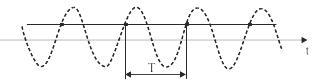
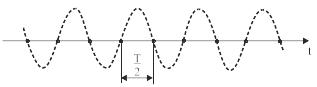
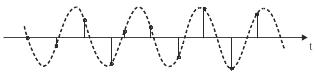
На примере синусоиды (рис. 6.9) рассмотрим, каким образом выбирается интервал дискретизации. Если соединить выделенные черным цветом точки выборки на рис. 6.9а, то форма синусоиды четко просматривается и видно, что интервал дискретизации достаточно мал. А что произойдет, если его расширить? На рис. 6.9б представлен случай, когда период сигнала и интервал дискретизации выборки совпадают. Видно, что значения выборки не отображают форму сигнала. Следовательно, выбранный интервал выборки слишком велик.

Исходный сигнал

Достаточно малый объем выборки

Интервал выборки Т

Интервал выборки Т/2

Интервал выборки меньший, чем Т/2

Рис. 6.9. Дискретизация синусоиды

Попробуем его уменьшить до половины периода сигнала, как показано на рис. 6.9в. В этом случае есть вероятность, что преоб­разуются только нулевые значения сигнала и полученная инфор­мация будет неполной. А если еще сузить интервал дискретизации выборки, как показано на рис. 6.9г, тогда будет более или менее возможно определить первоначальную форму синусоиды.

Теоретически обосновано, что по ряду значений выборки можно достоверно воспроизвести синусоиду (это возможно при условии, что ее период более чем в два раза превышает интервал выборки). Если установить связь выборки с частотой, то получится, что по отношению к синусоиде с частотой f_с необходимо следование значений выборки с частотой, большей чем 2f_с. Эта частота выборки 2f_с называется частотой Найквиста.

В отечественной литературе частота f_c определяется теоремой Котельникова, которая лежит в основе всей импульсной связи. Она показывает, при каких условиях передача непрерывной функции может быть сведена к передаче отдельных импульсов или кодовых комбинаций.

Теорема Котельникова (для функций с ограниченным спектром):

Функция с ограниченным спектром полностью определяется своими значениями, отсчитанными через интервалы 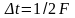, где F – ширина спектра функции.

Смысл теоремы Котельникова состоит в следующем: если требуется передать непрерывную функцию 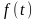с ограниченным спектром, то нет необходимости передавать все значения функции; достаточно передать отдельные мгновенные значения, отсчитанные через .

Таким образом, по материалам данного раздела можно сделать следующие основные выводы.

1. Сигнал – это физическая величина, содержащая информацию. Для анализа сигнала в первую очередь необходимо определить параметр, с помощью которого передается информация, ее единицу измерения и то, какую физическую величину отображает сигнал.

2. Если значение сигнала в какой-то момент времени можно точно предсказать, то сигнал называется детерминированным. Если же это невозможно, то сигнал называется случайным. Типичный пример детерминированного сигнала – синусоида. Ее параметрами являются угловая частота, амплитуда и фаза. Частота и период взаимосвязаны.

3. Периодическим сигналом называется сигнал, параметры которого не меняются при изменении времени на целое число периодов. Кроме синусоиды, существуют прямоугольный, пилообразный, треугольный и другие периодические сигналы. Одиночные сигналы бывают импульсные или затухающие.

4. Цифровой сигнал можно получить из аналогового методом дискретизации. Дискретизация по времени называется выборкой, а по значению величины сигнала – квантованием. Преобразование из аналогового сигнала в цифровой называется аналого-цифровым преобразованием.

5. В процессе оцифровки сигнала необходимо делать выборку с частотой большей, чем частота Найквиста. Частота Найквиста в два раза больше, чем самая высокочастотная составляющая сигнала. Это утверждение называют теоремой В. А. Котельникова, или теоремой отсчетов. Если проводить выборку с частотой ниже, чем частота Найквиста, возникают паразитные низкочастотные составляющие, не входящие в исходный сигнал. Преобразование цифрового сигнала в аналоговый называется цифро-аналоговым преобразованием.