5.4.8. Решение систем уравнений в MathCad
Методы решения систем уравнений рассмотрим те же, что и при решении уравнений: это вычислительный блок Given - Find и solve
1-й способ: вычислительный блок Given Find.
Численный метод применяется в том случае, если инженеру (или студенту) необходимо получить только лишь численные результаты своей работы. Тогда необходимо изначально задать значения всех «букв» и даже переменных. Переменные нужно задать в качестве начальных приближений. Эти начальные приближения нужны для корректной работы численных методов MathCad. При этом если начальное приближение не задано или задано не верно, очень большая вероятность, что решение найдено не будет.
2-й способ. Символьный метод применяют для нахождения выражения искомой переменной из данной системы. В этом случае не обязательно задавать все величины, входящие в систему. Достаточно просто записать все уравнения по порядку и затем найти решения. Следует отметить, что не всегда удается получить символьное выражение для переменной (ввиду сложности преобразований). За то численный результат машина найдет, если, конечно, он существует.
Приводим пример решения систем с помощью метода solve.
Этот метод очень хорошо подходит для получения корня в символьном виде. Записывается он так же как и для уравнений, с тем лишь отличием, что уравнения записываются в матрицу-столбец. Далее давится кнопка на панели Symbolic с надписью solve, и затем перечисляются все искомые переменные. Форма записи представлена в примере на рис. 5.2.
5.4.9. Программирование в MathCad
Составление программ – дело, как известно, не простое и почему-то очень нелюбимое многими студентами инженерных специальностей. На самом деле программирование – это очень удобная и полезная вещь в расчетах. В MathCad программа фактически является простой функцией и в конечном итоге просто числом. Сама же функция может работать по алгоритму, который Вы составите.
В MathCad программы составляются следующим образом. Допустим, есть некоторые исходные величины, которые необходимо определенным образом преобразовать и соотнести так, чтобы в результате получить требуемое.
Для практического пояснения приведем пример составления программы для матрицы (рис. 5.3).
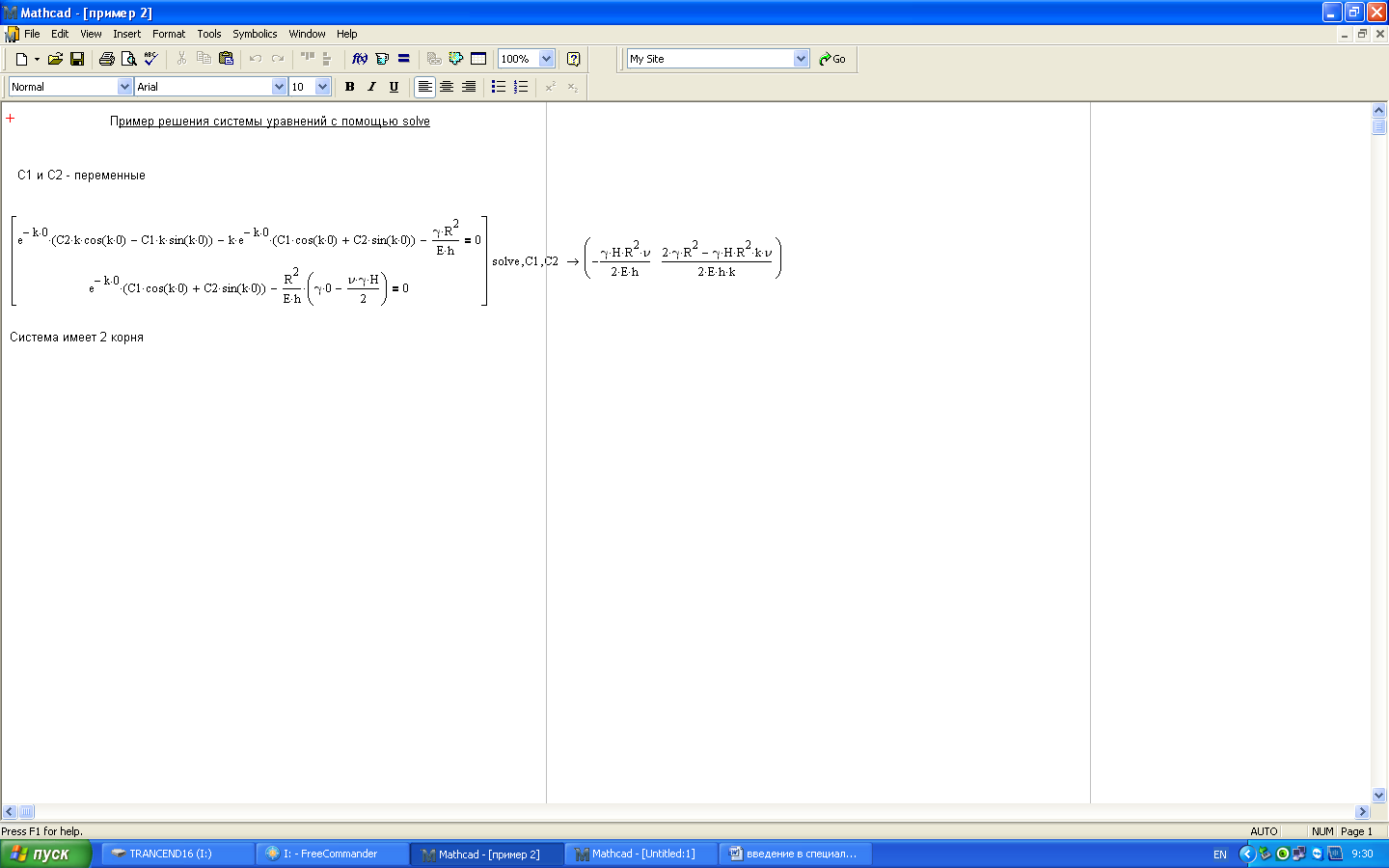
189 Рис. 5.2. Пример решения систем уравнений
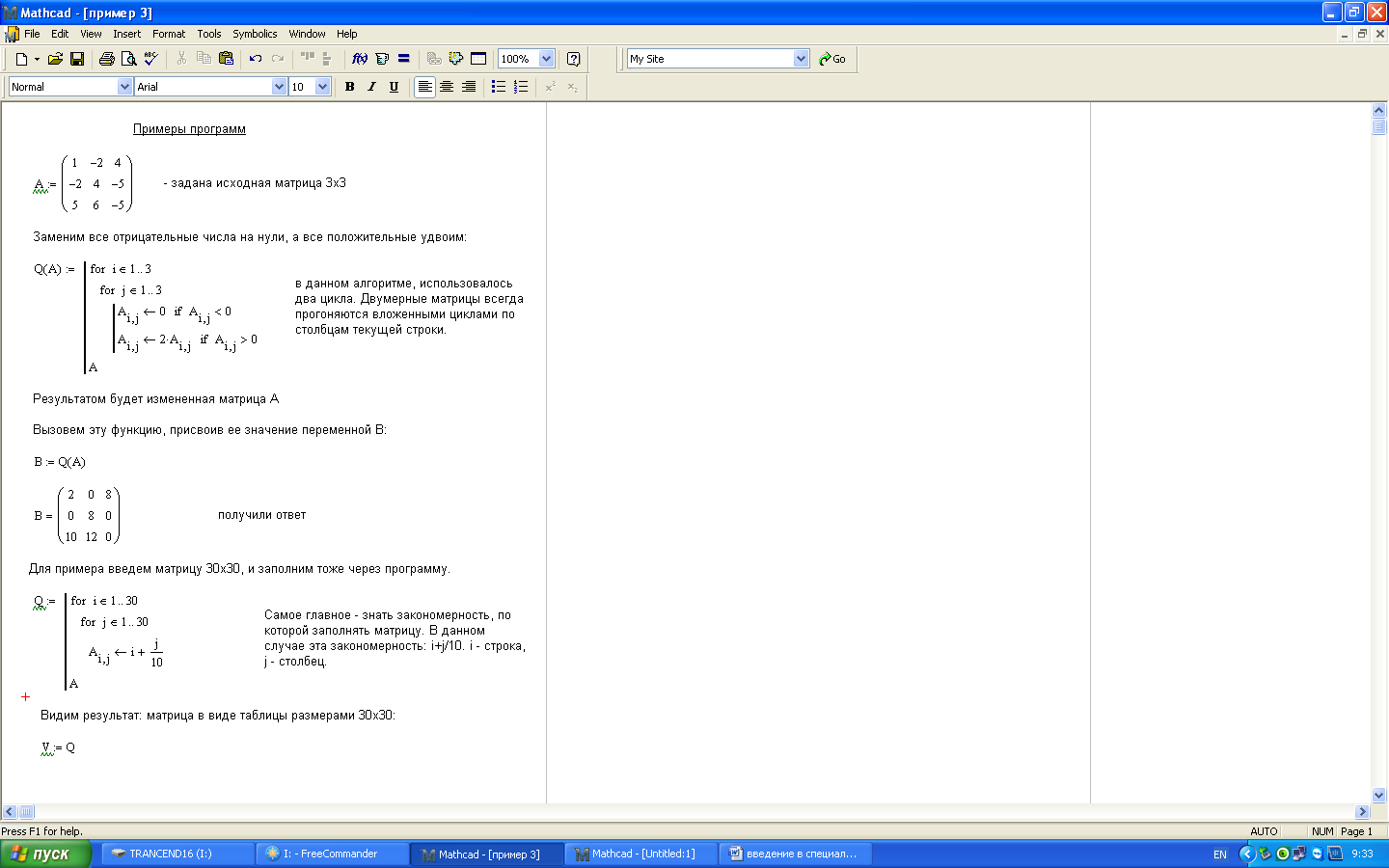
Рис. 5.3. Пример составления программы
КОНТРОЛЬНЫЕ ВОПРОСЫ
Для решения каких задач может быть использована программа Electronics Workbench?
Что содержат библиотеки системы Electronics Workbench?
Перечислите основные достоинства программы Electronics Workbench.
Для решения каких задач может быть использована среда программирования LabVIEW?
Что представляет собой виртуальный прибор среды LabVIEW?
Для решения каких задач может быть использован пакет прикладных программ MATLAB?
Перечислите типы программ, написанных на языке MATLAB.
В чем состоит основная особенность языка MATLAB?
Что представляют собой наборы инструментов MATLAB?
Для решения каких задач может быть использована система компьютерной алгебры Mathcad?
В чем заключается принцип WYSIWYG?
В чем основные достоинства системы Mathcad?
С какой целью используются пакеты расширений и библиотек системы Mathcad?
Как выполняется программирование в системе Mathcad?
В чем различия численных и символьных методов, применяемых в системе Mathcad?