2.4. Генерация колебаний синусоидального вида

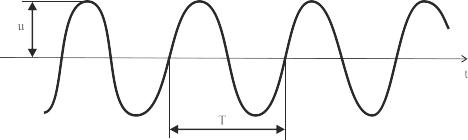
На рис. 2.4 представлен отрезок синусоиды. Он содержит участки длительностью Т, называемые периодом синусоиды.

Вся синусоида состоит из следующих друг за другом одинаковых фрагментов, длительностью Т. Количество таких фрагментов общей длительностью в одну секунду называется частотой синусоиды: . Единица частоты названа в честь Генриха Герца. Если в одну секунду выполняется десять полных периодов колебаний, то говорят, что частота равна .

Рис. 2.4. Колебание в виде отрезка синусоиды

Чтобы задать на синусоиде конкретную точку, весь период синусоиды делят на 360 равных частей (градусов). Количество градусов от начала периода до заданной точки на синусоиде называют фазой синусоиды.

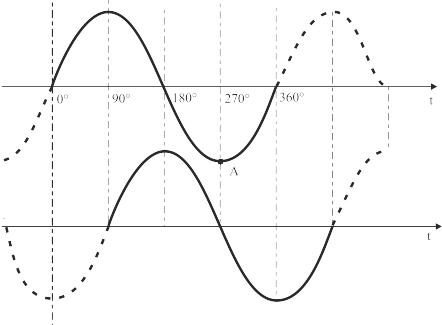
На синусоиде (рис. 2.5) расположена точка А. Фаза синусоиды в этой точке равна . Если имеются две синусоиды с одинаковой частотой, можно говорить о разности фаз этих синусоид. Например, разность фаз двух синусоид, показанных на рис. 2.5, равна .

В курсе «Радиотехнические цепи и сигналы» Вы узнаете, что большинство электрических и радиосигналов, например, в виде прямоугольного импульса, можно представить суммой синусоидальных сигналов, имеющих разные амплитуды, частоты и начальные фазы.

Набор этих синусоид называют спектром сигнала. Если спектр содержит информацию только об амплитудах этих синусоид, то говорят об амплитудно-частотном спектре сигнала, если только о фазах синусоид – то о фазочастотным спектре сигнала.

а) б)

Рис. 2.5. Сравнение фаз двух отрезков синусоиды одинаковой частоты

Мы живем в мире акустических, электромагнитных и других полей: музыки, речи, радиоволн, излучений в инфракрасном, оптическом, ультразвуковом и других диапазонах. Внутренняя структура этих полей хорошо интерпретируется лежащими в их основе синусоидальными колебаниями с разными амплитудами, частотами и фазами. Наши органы чувств: зрение и слух – обеспечивают восприятие окружающего мира именно с этих позиций.

Различные материальные тела обладают следующим интересным свойством. Преобразуем электрический ток синусоидальной формы определенной частоты f в механические колебания и подведем их к некоторому телу. Тело начнет колебаться с такой же частотой f. Затем прикрепим к телу преобразователь механических колебаний в электрические, которые будем контролировать с помощью осциллографа (рис. 2.6). На графиках А и В вертикальными линиями показаны амплитуды синусоидальных колебаний разных частот – от f₀ до f₁₁.

Рис. 2.6. Прохождение синусоидальных колебаний разных частот через тело 2:

1 – преобразователь электрических колебаний в механические; 3 – преобразователь механических колебаний в электрические; А – график амплитуд колебаний разных частот с выхода генератора; В – график амплитуд колебаний разных частот после их прохождения через тело

График А характеризует колебания с выхода генератора. Видно, что все они имеют одинаковые амплитуды. График В показывает амплитуды этих же колебаний после прохождения через тело 2. Видно, что амплитуда колебаний тела 2 зависит от частоты возбуждающих колебаний: сначала плавно нарастает, на частоте f₆ достигает максимального значения, а затем плавно спадает. Частота f₆ синусоидального колебания, при котором тело 2 колеблется с максимальным размахом, называется резонансной для тела 2. Конкретное значение резонансной частоты f_р определяется геометрическими размерами тела 2. Заметим, что огибающая амплитуд колебаний на рис. 2.6 (график В) называется амплитудно-частотной характеристикой тела 2.

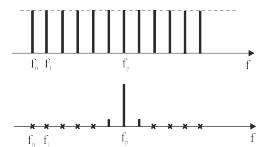
Скорость нарастания и спадания колебаний тела зависит от свойств материала, из которого изготовлено тело 2. Если материал вызывает большие потери энергии колебаний, то эти процессы будут происходить медленно, например, как показано на рис. 2.6. Если затухание колебаний при прохождении через тело 2 очень низкое, например, когда тело представляет собой кристалл кварца, то колебания будут происходить только на резонансной частоте f_р, а на колебания с другими частотами тело не будет реагировать (рис. 2.7). В таком случае говорят, что тело обладает хорошими резонансными свойствами.

Рассматривая внимательно рисунок 2.7, можно прийти к выводу, что такие материалы как кварц, обладающие очень малыми потерями энергии, при прохождении через них колебаний на резонансной частоте выполняют роль фильтров, т.е. пропускают синусоидальные колебания в очень узкой полосе частот и подавляют колебания всех остальных частот.

а) б)

Рис. 2.7. Прохождение синусоидальных колебаний с разными частотами через кристалл кварца: а) амплитуда колебаний, подводимых к кристаллу; б) амплитуда колебаний электрического тока в кристалле.

Тело 2 является примером механической колебательной системы. Кроме таких систем существуют широко применяемые в радиотехнике электрические колебательные системы. Примером такой системы является колебательный контур. Он представляет собой параллельно соединенные конденсатор С и катушку индуктивности L. Если в схеме на рис. 2.8 предварительно зарядить конденсатор, а затем с помощью переключателя П подключить его к катушке индуктивности, то в контуре возникнут синусоидальные колебания.

Рис. 2.8. Параллельный контур как электрическая колебательная система

Частота колебаний определяется значениями емкости С и индуктивности L. Чем меньше произведение LС, тем более высокую частоту будут иметь электрические колебания. Эти колебания вызваны обменом электрической энергии, запасенной в конденсаторе, с магнитной энергией, запасенной в индуктивности. Такие колебания называются свободными. Их энергия тратится в основном на разогрев провода катушки индуктивности, и поэтому со временем они постепенно затухают (рис. 2.9).

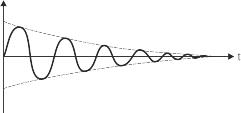
Рис. 2.9. Свободные колебания в контуре

Свободные колебания происходят на резонансной частоте f_р контура. Это означает, что если бы к колебательному контуру подводили от внешнего генератора синусоидальные колебания разных частот, но с одинаковой амплитудой (см. рис. 2.6 и 2.7), то колебания электрического тока в контуре имели бы максимальную амплитуду при подаче на контур колебаний от генератора на частоте

Цель данного раздела состоит в рассмотрении общих принципов построения генераторов периодических колебаний синусоидальной формы. Для этого мы предварительно охарактеризовали синусоиду как один из видов электрических сигналов, ввели понятие частотного спектра электрического сигнала произвольной формы и отметили, что такие сигналы можно представить суммой большого количества синусоид с разными частотами, амплитудами и разными фазами. Становится понятным, какую важную роль в теории сигналов играет синусоидальный сигнал: он является как бы атомом в пространстве сигналов, так как из комбинаций синусоидальных сигналов можно построить любой другой сигнал.

Далее было показано, что любое тело можно рассматривать в качестве колебательной системы. Амплитудно-частотная характеристика такой системы показывает, в какой степени ослабляются (затухают) колебания различных частот при их прохождении через тело. Каждая колебательная система характеризуется значением резонансной частоты, на которой происходит наименьшее ослабление подводимых к телу колебаний. На резонансной частоте возникают так называемые свободные колебания тела. Они происходят за счет накопленной в теле энергии и при отсутствии внешней вынуждающей силы. Поскольку в процессе свободных колебаний происходят потери энергии на теле на трение или разогрев тела, колебания с течением времени затухают.

Теперь чтобы перейти к рассмотрению принципа генерации синусоидальных колебаний, следует ознакомиться с влиянием обратных связей в колебательных системах, возникающих при подаче части энергии с выхода системы на ее вход.

Существуют два вида обратных связей – положительные и отрицательные. В результате действия положительной обратной связи уровень выходного сигнала увеличивается, а при действии отрицательной обратной связи этот уровень падает.

Эквивалентная схема генератора синусоидальных сигналов показана на рис. 2.10. Схема содержит резонатор в виде параллельного колебательного контура, настроенного на частоту f_р, усилительный каскад, во входную цепь которого включен резонатор, и цепь положительной обратной связи с выхода усилителя на колебательный контур и источник энергии, питающего усилитель.

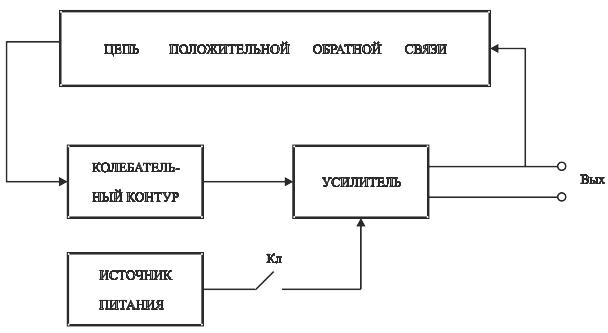
Рис. 2.10. Эквивалентная схема генератора электрических колебаний