Лабораторная работа 1.2

Определение момента инерции махового колеса и силы трения в опоре

Цель работы: определить момент инерции махового колеса и силы

трения в опоре.

Краткая теория

Закон сохранения энергии. В замкнутой системе энергия не исчезает и не возникает. Она только переходит из одной формы в другую.

Частным случаем этого закона является закон сохранения полной механической энергии. В замкнутой системе консервативных сил полная механическая энергия остается неизменной:

Е_кин+Е_пот = сonst,

где Е_кин= – кинетическая энергия, которой обладает любое тело массы m, движущееся со скоростью V;

Е_пот=mgh – потенциальная энергия тела, она определяется взаимным расположением тел h<<R_З.

Консервативными силами называются силы, работа которых не зависит от формы траектории, а зависит только от начального и конечного положения тела. Например, силы упругости, тяготения.

Диссипативными силами называют силы, работа которых зависит от длины и формы траектории. Например, силы трения.

Если в системе присутствуют диссипативные силы, то часть механической энергии переходит в тепловую.

Моментом инерции тела относительно данной оси вращения называется физическая величина, характеризующая меру инертности тела при изменении угловой скорости под действием вращающего момента. Момент инерции тела относительно данной оси вращения является величиной скалярной.

Моментом инерции материальной точки относительно произвольной оси называется произведение массы m этой точки на квадрат расстояния до оси:

J=mr².

Момент инерции твердого тела относительно какой–либо оси равен сумме моментов инерции всех точек тела относительно этой оси:

.

Для сплошного тела момент инерции относительно какой–либо оси вычисляется:

,

где  – плотность, dV – элементарный объем.

Так как момент инерции зависит от оси вращения, то при определении момента инерции необходимо указывать ось вращения.

Вращающееся тело обладает кинетической энергией вращательного движения:

,

где J – момент инерции тела, ω – его угловая скорость.

Теория метода и описание установки

Приборы и принадлежности: стойка, на которой закреплено маховое

колесо, линейка, секундомер, шнур с

грузом.

Целью работы является определение момента инерции махового колеса и силы трения в опоре.

М омент инерции махового колеса А и силу трения вала С в опоре можно определить при помощи прибора, изображенного на рис.1.

Маховое колесо приводится во вращательное движение грузом В. Груз В в начальный момент времени находится на высоте h_1, обладая потенциальной энергией mgh₁, где m – масса груза. Если предоставить возможность грузу падать с высоты h₁, то потенциальная энергия груза перейдет в кинетическую энергию поступательного движения груза E_k= , кинетическую энергию вращательного движения махового колеса и на работу по преодолению трения в опоре вала, A=f_трh₁. По закону сохранения энергии:

mgh₁= + + f_трh₁. (1)

Груз движется равноускоренно без начальной скорости. Скорость и ускорение соответственно выразятся:

. (2)

Угловая скорость махового колеса определится по формуле:

, (3)

где r – радиус вала, на который наматывается шнур груза.

Сила трения f_тр вычисляется следующим образом. Маховое колесо, вращаясь по инерции, поднимает груз на высоту h₂<h₁ и потенциальная энергия груза на высоте h₂ будет равна mgh₂. Груз не поднимается на первоначальную высоту, так как часть энергии тратится на работу по преодолению силы трения в опоре:

mgh₁ – mgh₂=f_кр(h₁+h₂). (4)

Откуда сила трения равна:

. (5)

Подставив в (1) выражения для V, , f_тр из (2,3,5) получим:

,

преобразовав, получим:

.

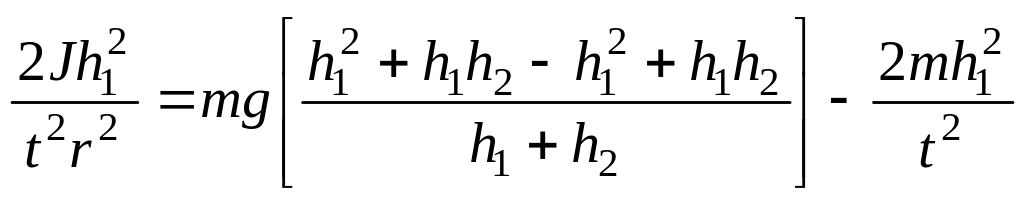Сделав соответствующие преобразования окончательно получим рабочую формулу :

(6)