Тема 4. АЛГЕБРА ЛОГИКИ

Цели и задачи изучения темы

В данной теме изучаются основы логических алгебр.

4.1. Логические функции. Алгебра Буля и алгебра Жегалкина.

4.1.1. Способы задания логических функций

Функция , зависящая от n переменных , называется логической или переключательной, если функция и любой из ее аргументов принимают значения только из множества {0,1}. Аргументы логической функции также называются логическими.

Рассмотрим три способа задания логической функции: матричный (табличный), геометрический и аналитический. При матричном способе логическая функция n переменных задается таблицей истинности, в левой части которой перечислены все наборов значений переменных, а в правой части – значение функции на этих наборах. Например, табл. 4.1 задает функцию трех переменных .

Таблица 4.1

Номер набора
0	0	0	0	0
1	0	0	1	1
2	0	1	0	1
3	0	1	1	1
4	1	0	0	0
5	1	0	1	1
6	1	1	0	0
7	1	1	1	0

Двоичный набор можно рассматривать как целое число N: , называемое номером набора . Поэтому иногда в таблице истинности логической функции наборы представляются их номерами. Часто для сокращения записи логическую функцию задают вектором , в котором координата представляет собой значение функции на наборе (на наборе с номером i), т.е. логической функции взаимно однозначно соответствует двоичный вектор длины , следовательно, существует различных логических функций от n переменных. Вектор также иногда задают в виде его десятичного эквивалента. Таким образом, при задании логической функции (см. табл. 4.1) можно использовать запись (01110100) или 116.

Логические функции, зависящие от большого числа переменных, задавать таблицей истинности неудобно в силу ее громоздкости. Поэтому, для задания функций многих переменных удобно использовать модификацию таблицы истинности. Для этого множество из n переменных функции разбивается на два подмножества и . В этом случае, n-мерное пространство с образующими , представляется в виде декартова произведения двух пространств  с образующими и соответственно (в геометрическом смысле каждый двоичный набор , есть n-мерный вектор, определяющий точку n-мерного пространства).

Тогда логическую функцию можно задать в виде двумерной таблицы: каждому значению переменных , ,..., взаимно однозначно соответствует строка таблицы, столбцу – значения переменных , ,..., и на пересечении i-й строки и j-го столбца, взаимно однозначно соответствующем точке n-мерного пространства с образующими , записывается значение функции в этой точке. Например, функция, представленная табл.4.1, может быть задана табл.4.2, где множество разбито на два подмножества и .

Таблица 4.2

	00	01	10	11
0	0	1	1	1
1	0	1	0	0

При геометрическом способе логическая функция задается с помощью гиперкуба ( n-мерного куба ).

Гиперкубом называется граф, каждая вершина которого взаимно однозначно соответствует точке пространства - двоичному вектору (набору), и две вершины соединены ребром, если соответствующие им двоичные векторы отличаются в одном и только одном разряде.

Отмечая вершины куба, в которых функция принимает единичное (либо нулевое) значение, получим геометрическое представление функции. Например, логическая функция, заданная табл.4.1, геометрически представляется 3-мерным кубом на рис.4.1. В данном примере черным цветом закрашены вершины куба, в которых функция принимает единичное значение.

Если на некоторых наборах значений переменных логическая функция не определена (т.е., на данном наборе значение функции может быть как 0, так и 1), то она называется частичной. Доопределением частичной функции f называется всякая (всюду определенная) логическая функция, совпадающая с f там, где значения f заданы. В табл. 4.3 приведена частичная функция f и все возможные ее доопределения , , , .

При задании частичной функции обычно перечисляют наборы из области ее определения и указывают значения функции на каждом из них (табл. 4.4). Часто используется задание в виде двух таблиц, в одной из которых перечисляются наборы, где функция равна 1, а в другой – наборы с нулевым значением функции.

Прежде чем рассматривать аналитический способ задания логических функций, рассмотрим наиболее употребляемые логические функции одной и двух переменных (элементарные функции). Функции одной переменной представлены в табл.4.5, некоторые функции двух переменных – в табл.4.6. Приведем обозначения и названия этих функций.

1. Функции (x)=0 и (x)=1 называются соответственно тождественным нулем и тождественной единицей. Заметим, что и не зависят от переменной x, поэтому их иногда рассматривают как функции, зависящие от пустого множества переменных. Функцию еще называют константой 0, а – константой 1. Переменная x в данном случае является фиктивной. В общем случае переменная 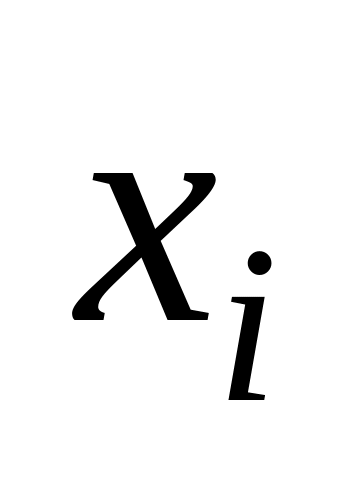в функции называется фиктивной (несущественной), если

=

при любых значениях остальных переменных.

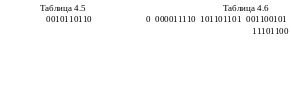
2. Функция (x) называется тождественной функцией и обозначается через x.

3. Функция (x) называется отрицанием x, обозначается ,  x, x’ и часто читается "не x".

4. Функция называется конъюнкцией, обозначается & ,  ,  , , или min( , ) и часто читается « и ».

5. Функция называется дизъюнкцией, обозначается  , + или max( , ) и часто читается « или ».

6. Функция называется суммой по модулю 2, обозначается  ,  и часто читается " плюс ". Так как данная функция равна 1, когда ее аргументы различны, и равна 0, когда они равны, то ее иногда называют неравнозначностью.

7. Функция называется эквивалентностью или равнозначностью. Ее обозначения:  ,  или  , читается " эквивалентно ".

8. Функция называется импликацией. Обозначения  ,  ; читается "если , то " или " имплицирует ".

9. Функция называется штрихом Шеффера, обозначается  и часто читается "не и ".

10. Функция называется стрелкой Пирса (функция Вебба), обозначается  , читается "не или ".

Теперь рассмотрим аналитический способ задания логической функции, при котором логическая функция f задается суперпозицией других функций (формулой).

Суперпозицией функций называется функция f, полученная с помощью подстановок этих функций друг в друга и переименования переменных, а формулой называется выражение, описывающее эту суперпозицию. Понятие суперпозиции очень важно в алгебре логики, поэтому рассмотрим его более подробно.

Пусть дано множество (конечное или бесконечное) исходных функций . Символы переменных будем считать формулами глубины 0. Формула F имеет глубину , если F имеет вид , где , t - число аргументов , а – формулы, максимальная из глубин которых равна k. называется подформулами F; называется внешней или главной операцией формулы F. Все подформулы формул также называются подформулами F. Например, (x), и – это формулы глубины 1, а – формула глубины 3, содержащая одну подформулу глубины 2 и две подформулы глубины 1.

В дальнейшем конкретные формулы, как правило, будут иметь более привычный вид, при котором знаки функций стоят между аргументами. Такую запись называют инфиксной, то есть формулу вида f (x,y) записывают либо как (x f y), либо как x f y, а формулу f (x) - как (f x) или f x. При этом символы f называют связками. Обычно в качестве связок употребляются символы из множества G={,&,,,,,,}, то есть символы, обозначающие рассмотренные выше элементарные функции.

Например, если обозначает отрицание ( ), – дизъюнкцию (), – конъюнкцию (&), а – импликацию (), то приведенная ранее формула примет вид ((x)(z(x&y))).

Для сокращения записи формул над множеством связок G принято следующее соглашение:

а) внешние скобки у формул опускаются;

б) формула (F) записывается в виде ;

в) формула ( & ) записывается в виде  или ;

г) считается, что связка  сильнее любой двухместной связки из G;

д) связка & считается сильнее, чем любая из связок , , , , , .

Эти соглашения позволяют записать рассматриваемую формулу в виде

Употребляется и смешанная запись формул, например, xf(y,z) или .

Всякая формула, выражающая функцию f как суперпозицию других функций, задает способ ее вычисления (при условии, что известно, как вычислить исходные функции). Вычислим, например, формулу на наборе x=0, y=1, z=1. Получим (используя табл. 4.5 и 4.6): xy=0; zxy=z0=1; =1; (zxy)=11=1.

Таким образом, формула каждому набору значений аргументов ставит в соответствие значение функции и, следовательно, может служить наряду с таблицей способом задания и вычисления функции. В частности, по формуле, вычисляя ее на всех наборах, можно восстановить таблицу функции.

О формуле, задающей функцию, также говорят, что она реализует или представляет эту функцию. Если функция f частична, то считается, что формула реализует f, если она реализует какое-либо ее доопределение.

В отличие от табличного и геометрического задания представление данной функции формулой не единственно. Например, если в качестве исходного множества связок зафиксировать множество {,&,}, то функцию штрих Шеффера ( в табл. 4.6) можно представить формулами:  и , а функцию стрелка Пирса ( ) - формулами и .

Формулы, представляющие равные функции, называются эквивалентными или равносильными. Эквивалентность формул обозначается знаком равенства, поэтому можно записать

, (4.1)

. (4.2)

Для того, чтобы для двух данных формул выяснить, эквивалентны они или нет, можно по каждой формуле восстановить таблицу истинности функции, а затем полученные две таблицы сравнить. Этот метод требует вычислений (если считать, что обе формулы зависят от n переменных) и на практике оказывается слишком громоздким. Существуют и другие методы установления эквивалентности формул и получения новых формул, эквивалентных исходной. Эти методы будут рассмотрены в следующих разделах.

Задания для самостоятельной работы к разд.4.1.1

1. Весом набора называется число единиц в данном наборе. Сколько существует наборов веса k?

2. Найти номера наборов (1001), (01101), (110010).

3. Найти вектор длины 6, являющийся двоичным разложением числа 19.

4. Восстановить таблицу истинности функции 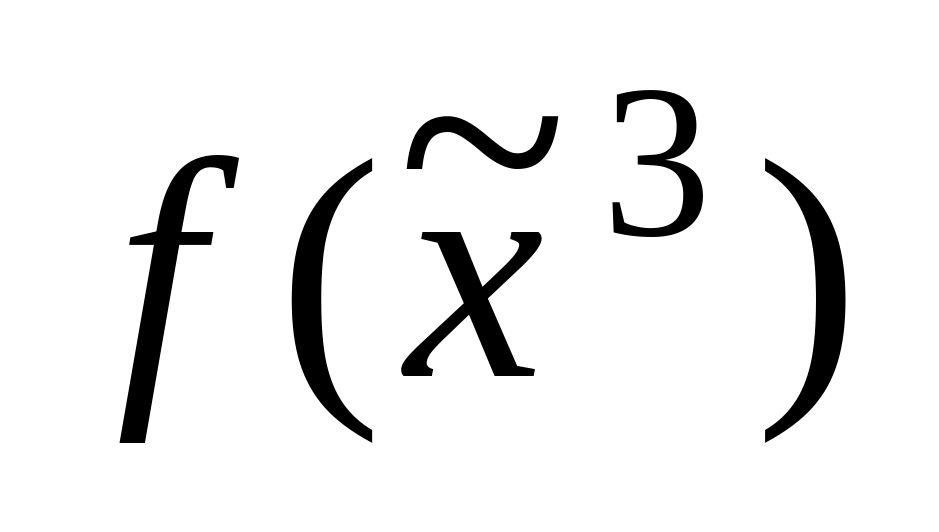=41.

5. Частичная функция не определена на k наборах. Сколько существует различных доопределений данной функции?

6. Выяснить, какие из ниже перечисленных выражений являются формулами над множеством связок {,&,,}:

1) xy; 4) (xy)x; 7) (xz);

2) (x&)z; 5) (x&yy)y; 8) (x(y&(x)));

3) (xy)x; 6) y&(z(xy)).

7. Проверить справедливость формул (4.1) и (4.2).

8. Построить таблицу функций, реализуемых следующими формулами:

1) 3)

2) 4)

9. Эквивалентны ли формулы и ?

1)

2)

3)

4)

10. Написать программу, определяющую вес двоичного набора, который хранится в машинном слове b. Содержимое b интерпретируется машиной как беззнаковое целое.

Указание. Необходимо организовать подсчет единичных разрядов в машинном слове. Это можно сделать, выполнив n раз сдвиг влево (вправо) и анализ (n-1)-го (0-го) бита слова, где n - длина слова. Число шагов такого алгоритма всегда равно n и не зависит от веса двоичного набора. Более оригинальный алгоритм подсчета числа единичных разрядов в слове всегда делает k шагов, где k – число единиц в слове. Он основан на том, что операция b:= b and (b-1) уничтожает в b самую правую единицу, т.о., после того, как указанная операция будет выполнена k раз, слово станет нулевым (b=0).

4.1.2 Булева алгебра. Эквивалентные преобразования формул. Двойственные и самодвойственные функции. Алгебра жегалкина

Алгебра , основным множеством которой является все множество логических функций, а операциями – дизъюнкция, конъюнкция и отрицание, называется булевой алгеброй.

Операции алгебры А называют булевыми операциями. Формулы над множеством {,&,} также называют булевыми формулами. Тот факт, что любая логическая функция может быть представлена в виде формулы над {,&,}, будет доказан ниже.

Рассмотрим основные свойства булевых операций.

Ассоциативность:

а) ; б) . (4.3)

Коммутативность:

а) ; б) . (4.4)

Дистрибутивность конъюнкции относительно дизъюнкции:

. (4.5)

Дистрибутивность дизъюнкции относительно конъюнкции:

. (4.6)

Идемпотентность:

а) ; б) . (4.7)

Двойное отрицание:

. (4.8)

Свойства констант:

а) x&1=x; б) x&0=0; в) x1=1;

г) x0=x; д) =1; е) =0. (4.9)

Правила де Моргана:

а) ; б) . (4.10)

Закон противоречия:

. (4.11)

Закон "исключения третьего":

. (4.12)

Соотношения (4.3) – (4.12) можно проверить указанным ранее стандартным методом – вычислением обеих частей равенств на всех наборах значений переменных. Очевидно, что результат вычисления не зависит от того, как получены значения переменных, входящих в эти равенства, то есть, от того, являются ли эти переменные независимыми, или, в свою очередь, получены в результате каких-то вычислений.

Поэтому равенства (4.3) - (4.12) остаются справедливыми при подстановке вместо переменных любых логических функций и, следовательно, любых формул, представляющих эти функции. Важно лишь соблюдать следующее правило подстановки формулы вместо переменной: при подстановке формулы F вместо переменной x все вхождения переменной x в исходное соотношение должны быть одновременно заменены формулой F.

Сформулируем также правило замены подформул, которое позволяет, используя эквивалентные соотношения, получать формулы, эквивалентные данной. Пусть , тогда, если какая-либо формула F содержит в качестве подформулы, то замена на не изменяет F.

Подчеркнем разницу между правилами подстановки и замены. При подстановке переменная заменяется на формулу; формула может быть любой, но требуется одновременная ее подстановка вместо всех вхождений переменной. При замене подформул может быть заменена любая подформула, однако, не на любую другую, а только на эквивалентную ей. При этом, замена всех вхождений исходной подформулы не обязательна.

Такие преобразования, использующие эквивалентные соотношения и правило замены, называются эквивалентными преобразованиями.

Запас эквивалентных соотношений можно расширить с помощью правила подстановки.

Пример 4.1. Возьмем соотношение (4.10а) и подставим вместо . Получим , то есть две формулы, не эквивалентные исходным, но эквивалентные между собой. Если же в правой части нового соотношения заменить формулой , эквивалентной ей в силу (4.10а), а в полученной подформуле заменить на эквивалентную ей в силу (4.8) формулу , то все формулы в построенной цепи преобразований эквивалентны.

Рассмотрим некоторые из эквивалентных соотношений в булевой алгебре, и как они получаются путем использования уже рассмотренных соотношений.

Правила поглощения:

а) ; б) . (4.13)

Для доказательства первого равенства используются последовательно соотношения (4.9а), (4.5), (4.9в), (4.9а): . Второе равенство доказывается с помощью (4.5), (4.7а) и первого равенства: .

Правило склеивания:

. (4.14)

Доказательство: .

Правило обобщенного склеивания:

. (4.15)

Доказывается с помощью расщепления, то есть, применения (4.14) в обратную сторону и поглощения (4.13а): .

Правило вычеркивания:

а) ; б) ; (4.16)

Доказательство: ;

.

Эквивалентные преобразования являются мощным средством доказательства эквивалентности формул, как правило, более эффективным, чем их вычисление на наборах значений переменных.

Пример 4.2. Эквивалентны ли формулы и ?

; .

Используя последовательно (4.18), (4.15), (4.14) и (4.13а), получаем

= = = = .

Теперь преобразуем с помощью соотношений (4.10а), (4.10б) и (4.4б):

= .

Т.о., формулы и эквивалентны.

Для более легкого запоминания рассмотренных соотношений, и получения новых можно использовать принцип двойственности.

Функция называется двойственной к функции , если = .

Может оказаться, что функция двойственна самой себе, т.е., = . В этом случае она называется самодвойственной функцией.

Принцип двойственности заключается в следующем: если в формуле F, представляющей функцию f, все знаки функций заменить соответственно на знаки двойственных функций, то полученная формула F* будет представлять функцию f*, двойственную f.

Для формул над множеством {0,1,,&,} принцип двойственности может быть сформулирован так: для получения формулы F*, двойственной формуле F, достаточно в формуле F всюду заменить 0 на 1, 1 на 0, & на ,  на &.

Например, из соотношения применением принципа двойственности получается соотношение .

Пример 4.3. Является ли функция двойственной к функции ?

Проверку двойственности и самодвойственности функций можно производить непосредственно по их таблицам истинности или с помощью эквивалентных преобразований. Проведем проверку по таблицам истинности (табл. 4.6, , ). Имеем . Т.о. функция f двойственна к функции g.

Пример 4.4. Является ли функция самодвойственной?

Для ответа на поставленный вопрос с помощью эквивалентных преобразований докажем, что = .

=

Заметим, что тот же результат можно было получить, используя принцип двойственности, сформулированный для формул над множеством {0,1,,&,}. Продолжим эквивалентные преобразования:

= = = = .

Т.о., = , следовательно, функция f самодвойственная. Рассмотрим еще одну алгебру над множеством логических функций. Алгебра над множеством логических функций с двумя бинарными операциями & и  называется алгеброй Жегалкина. В алгебре Жегалкина выполняются следующие соотношения:

; (4.17)

; (4.18)

; (4.19)

, (4.20)

а также соотношения булевой алгебры, относящиеся к конъюнкции и константам (4.3а), (4.4а), (4.7а), (4.9а), (4.9б).

Отрицание и дизъюнкция выражаются так:

; (4.21)

. (4.22)

Любая булева функция может быть представлена формулой над множеством . Это следует из того, что любая булева функция может быть представлена формулой над множеством {,&,} (см. разд. 4.2) и того, что функции {, &, } выражаются через функции {&,,1} (см. (4.21), (4.22)).

Пример 4.5. Эквивалентны ли формулы и ?

Преобразуем . Используя соотношение (4.22), получаем

.

Далее, с помощью соотношения (4.21) избавимся от отрицаний и раскроем скобки (4.18):

.

Используя соотношения (4.19) и (4.20), окончательно получаем:

.

Т.о., формула эквивалентна формуле .