2. Loogika seadmete minimeerimine.

2. 1. Lf minimeerimine Veitch`I diagrammide ja Karnaugh kaartide alusel.

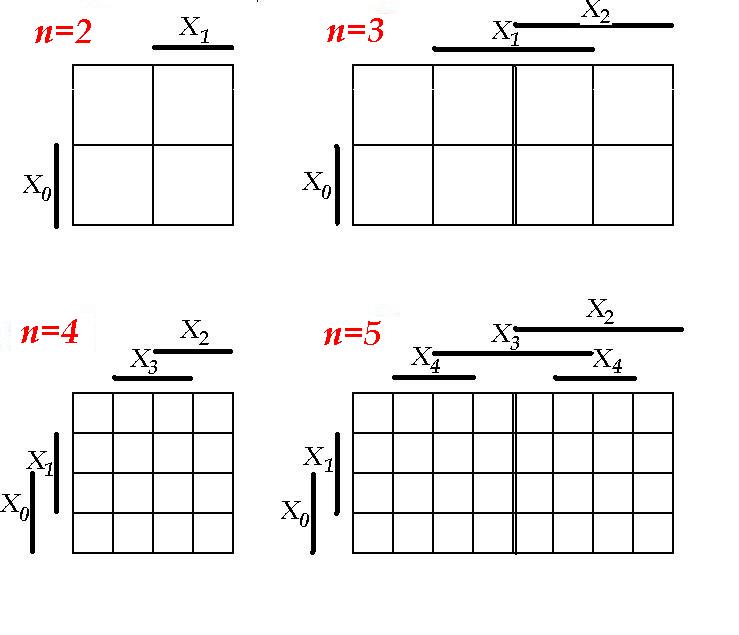
Kaardid ja diagrammid → ruudulised tabelid; ruudude arv → 2ⁿ,

kus n – vahelduvate kogus.

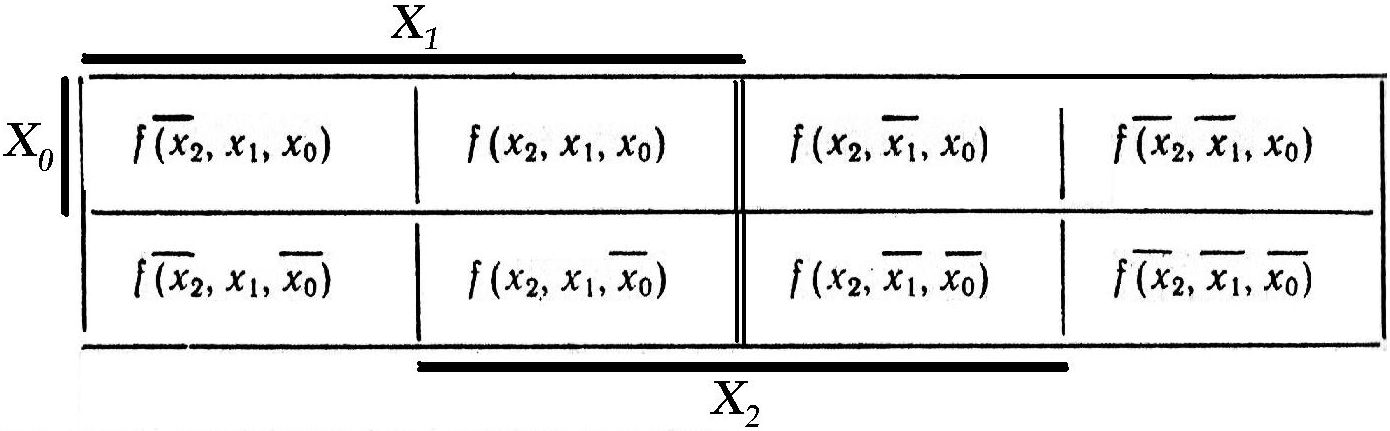
Veitch`i diagrammid:

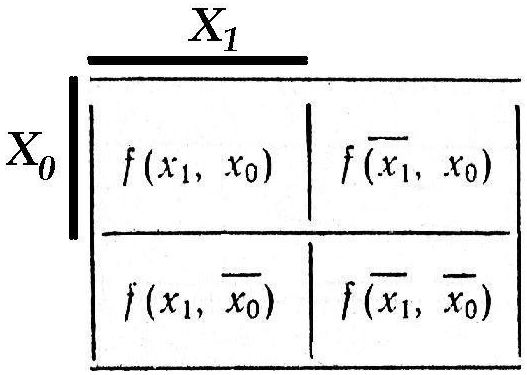n = 2, 3, 4

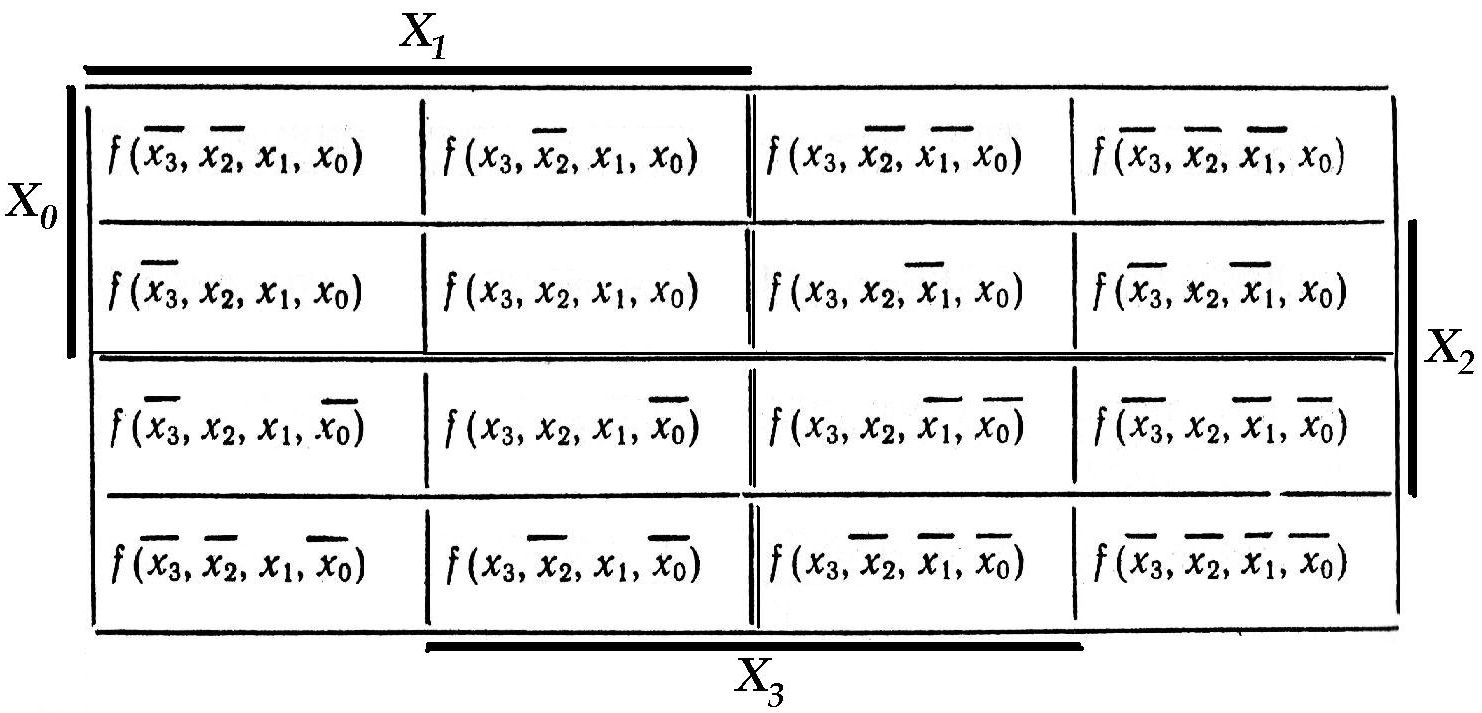
Karnaugh kaardid:

K.T. Nr.1

Kaartide täitmine.

2.2. Täielikult määratud LF minimeerimine.

Algoritm:

→ Veitch`i (Karnauh) kaardile on peale kantud n-muutuvatega LF. Tuleb välja valida, eraldada, täisnurgalised piirkonnad (kontuurid, katted), mis ühendavad kõik LF tähendused (loogika 1 või 0 järgi).

→ Iga piirkond, kontuur, peab sisaldama 2^k ruutu, kus k – täisarv.

→ Eraldatud piirkonnad võivad ristuda. Teisiti: mõned ruudud võivad kuuluda erinevatele piirkondadele (kontuuridele).

→ Saadud kontuuridest valida minimaalne arv maksimaalselt suuri kontuuri, mis sisaldavad kõik LF tähendused.

→ Loogikaliselt summeerida implekantid, mis vastavad valitud kontuuridele. Saadud summa ongi minimaalne disjunktiivne normaalne vorm (MDNV) juhul, kui kirjeldatud protseduur oli tehtud 1 – järgi.

Kuna minimeeritav LF oli täielikult määratud, siis juhul, kui protseduur oli läbiviidud 0 – järgi, tulemuseks on minimaalne konjuktiivne normaalne vorm (MKNV).

Näide

Minimeerida LF Veitch`i kaardi abil.

Koostame (täidame) Veitch`i kaart:

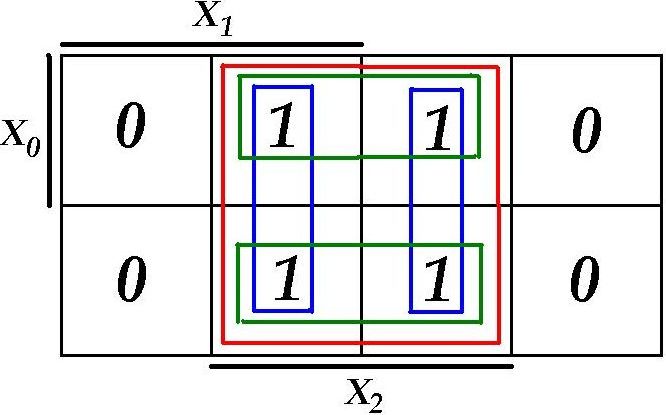
Saadud kontuurid (katted): П =

П =

П =

Lõpptulemus: Z(X) = X₂

K.T. Nr.2

Minimeerida täielikult määratud LF.

2.3. Mittetäielikult määratud LF minimeerimine.

Näide

LF on etteantud tabelina:

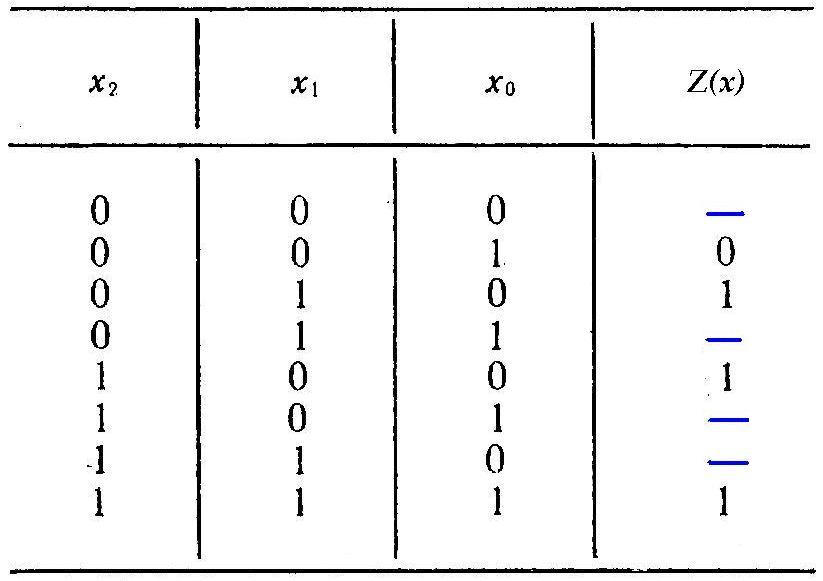
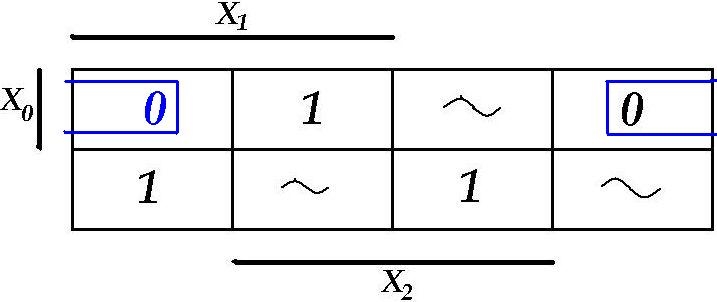
Tabeli alusel koostame LF avaldis ja Veitch`i kaart:

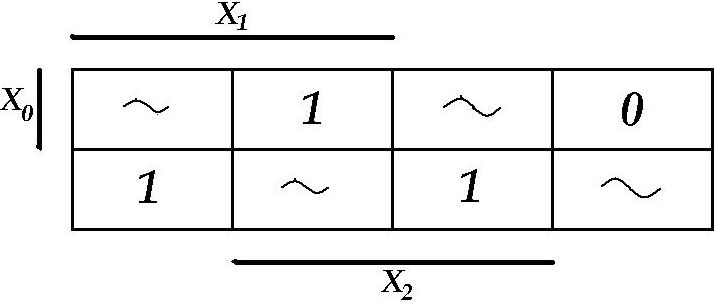
Vaatame üle kõik minimeerimise võimalused:

Oletame, et: Z(000) = 1, Z(110) = 1

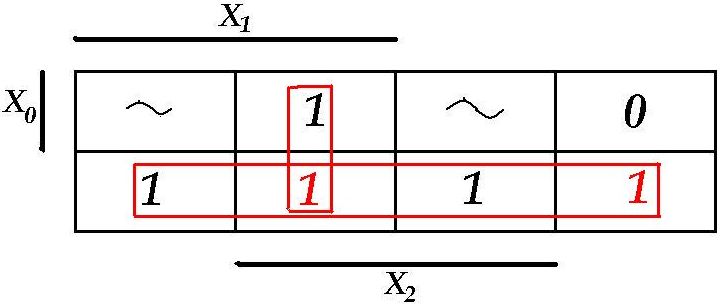
Oletame, et: Z(000) = 1, Z(110) = 1, Z(011) = 1

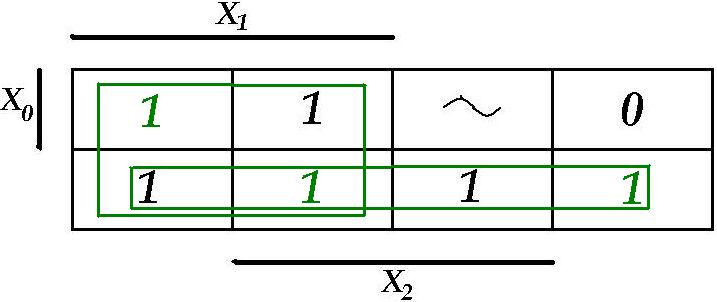
Oletame, et: Z(000) = 1, Z(110) = 1, Z(101) = 1

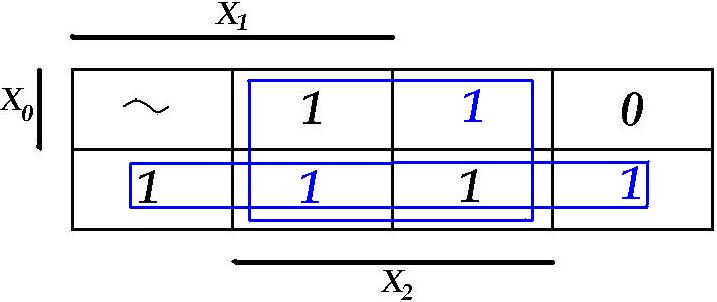
Oletame, et: Z(011) = 1, Z(101) = 1, Z(110) = 1

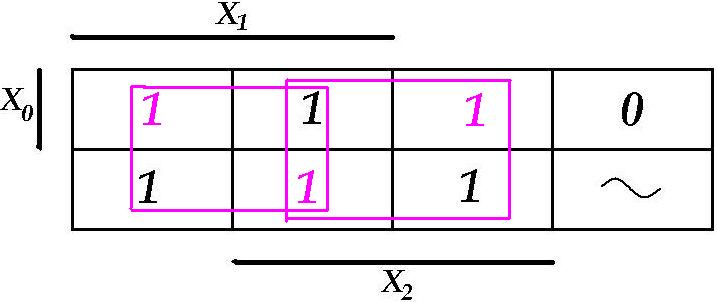
Etteantud LF minimeerimine „0“ – tähenduste järgi viib järgmistele avaldistele:

või

Oletame, et: Z(000) = 0

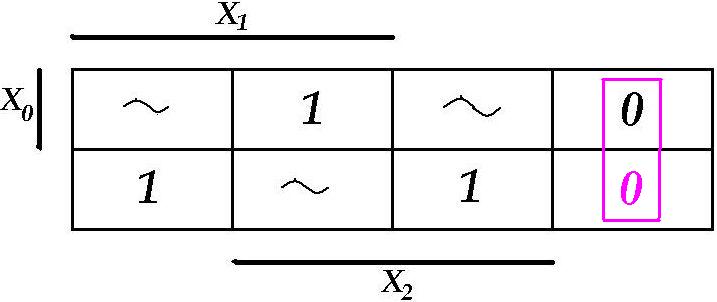
, või vastavalt De Morgan`i teoreemile:

Oletame, et Z(101) = 0

või
Oletame, et Z(011) = 0

või

K.T.Nr.3

Minimeerida mittetäielikult määratud LF.

3. Kombinatsioon – loogikaseadmed (kls).

3.1. Loogikaseadmete süntees etteantud baasi alusel.

Funktsionaalselt täieliku süsteemi NING, VÕI, EI tavaliselt

ei kasutata. Praktikas kasutakse NING-EI, VÕI-EI või isegi ainult ühte nendest.

Selle baasi abil võib esitada ükskõik missugust LF. Kasutamisel on kaks tehnilist võtet:

→ kahekordne inverteerimine (tervet LF või tema osa)

→ De Morgan`i teoreemide kasutamine

Näide

On antud LF:

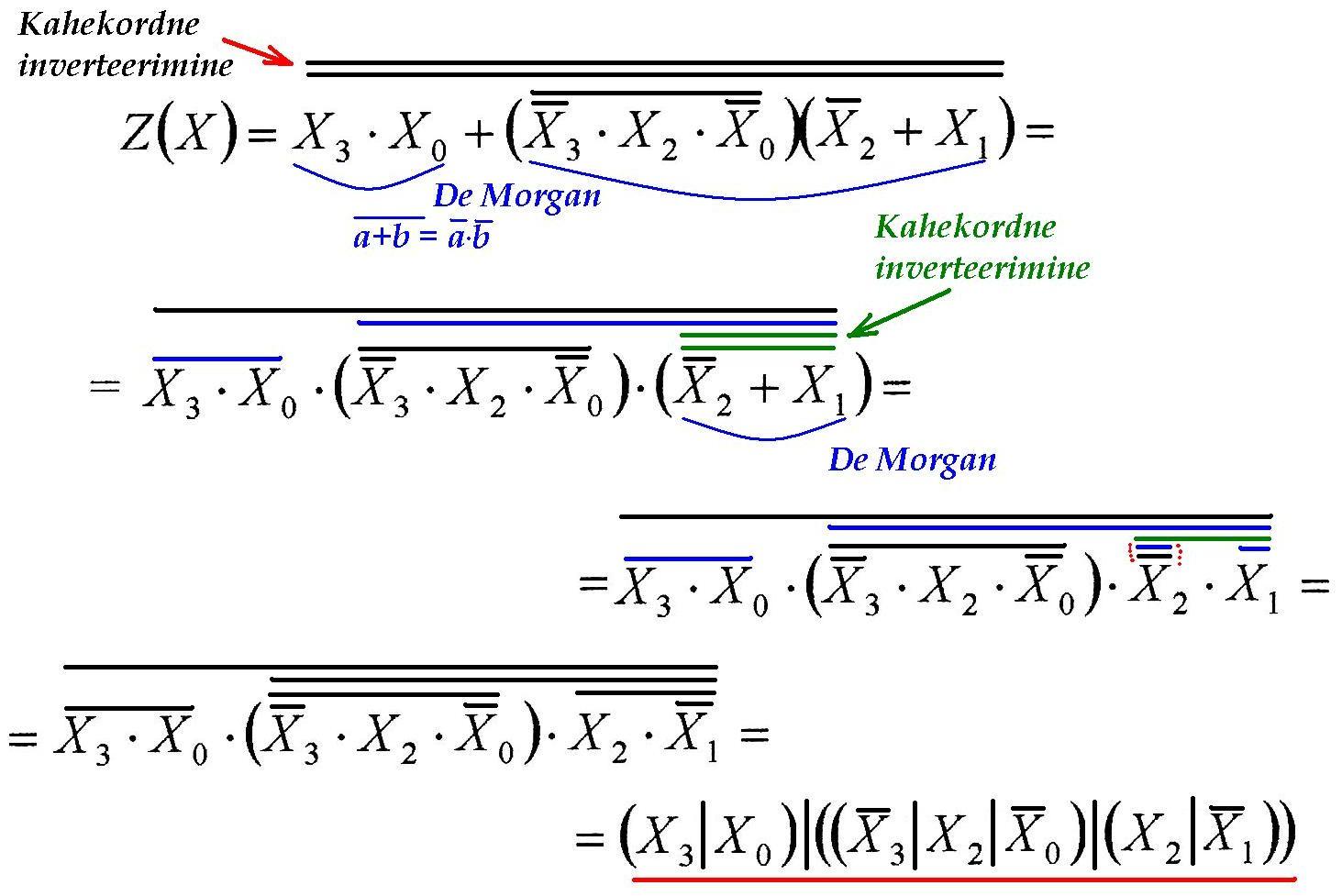
Vaja üle minna NING-EI baasi peale:

On vaja üle minna VÕI-EI baasi peale:

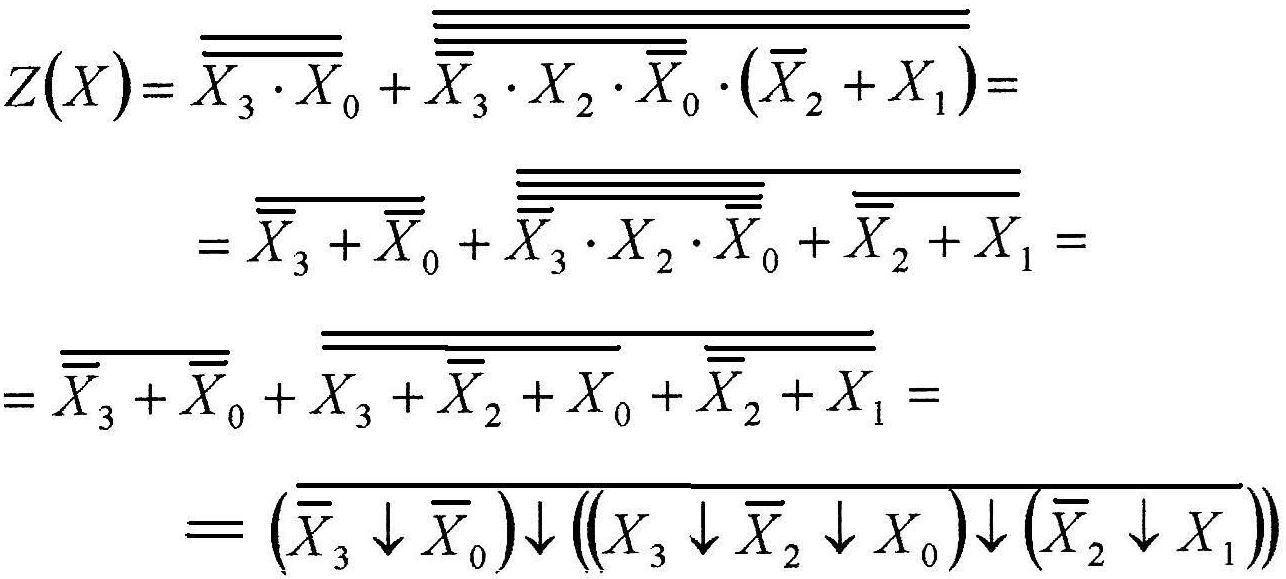
3.2. Loogikaseadmete ehitamine raalsete elementide

baasil.

Tavaliselt on ette antud ka LE sisendite arv. Sel juhul võivad esineda järgmised situatsioonid:

1. LE sisendite arv on suurem, kui LF vahelduvate (LS sisendsignaalide) arv;

2. LE sisendite arv on väiksem, kui LF vahelduvate arv.

→ LE sisendeid on rohkem, kui tarvis

Aktiivne loogikanivoo → sisendvahelduva tähendus, mis määrab ühetähenduslikult LE väljundsignaali.

Loogikaoperatsioonide tõesuste üldistatud tabel:

Tabelist on näha, et:

NING-EI → 0 – aktiivne, 1- passiivne;

VÕI-EI → 1- aktiivne, 0-passiivne.

Järeldus:

1. Vähendada LE sisendite faktilist arvu võib andes kasutamata sisenditele passiivsed loogikakonstantid. 0→VÕI-EI; 1→NING-EI.

2. Kuna on teada: 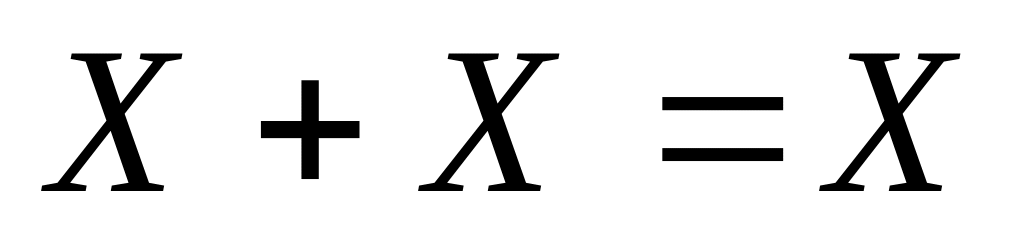ja , siis mitmele LE sisendile võib anda ühte ja sama loogikavahelduvat.

Veel järeldused:

1. Kui LE kõik sisendid saavad ühe ja sama signaali, siis LE muutub invertoriks.

2. Kui n-1 (n – sisendiga LE) sisendile anda passiivsed loogikasignaalid, siis n-sisendi suhtes LE muutub invertoriks.

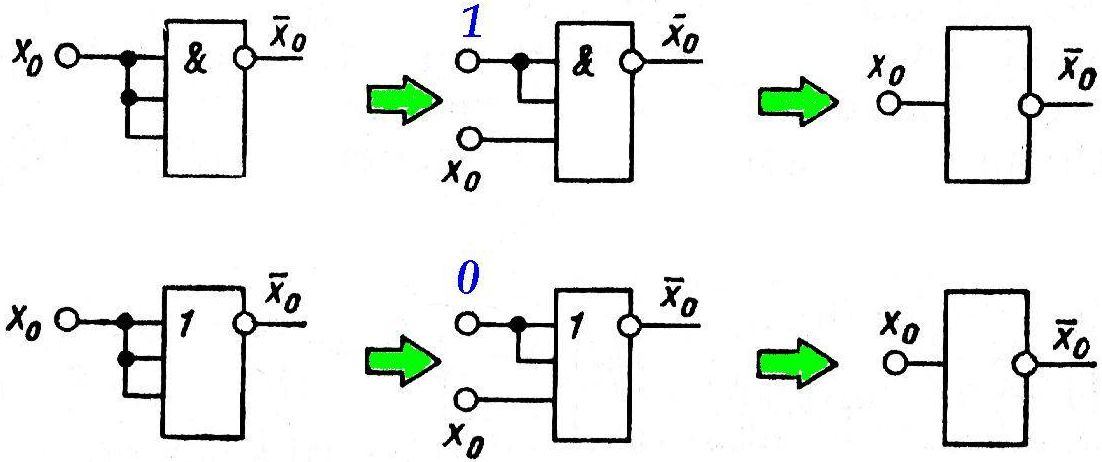
→ LE sisendeid on vähem, kui tarvis

a) MDNV ei sisalda ühiseid loogikavahelduvaid.

Sel juhul tuleb kasutada järgmised identsused:

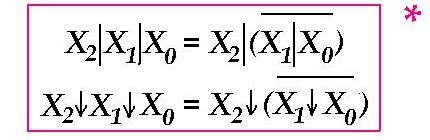
Tõestame esimest nendest: ↓kahekordne invert.

Sisendsignaale (vahelduvaid) * võib olla ka rohkem. Näiteks:

Näide

On antud LF ja tema realisatsioon:

Vaja aga üle minna 2VÕI-EI elementide peale. Teeme LF topelt inverteerimist:

Realisatsioon „2VÕI-EI“ baasil:

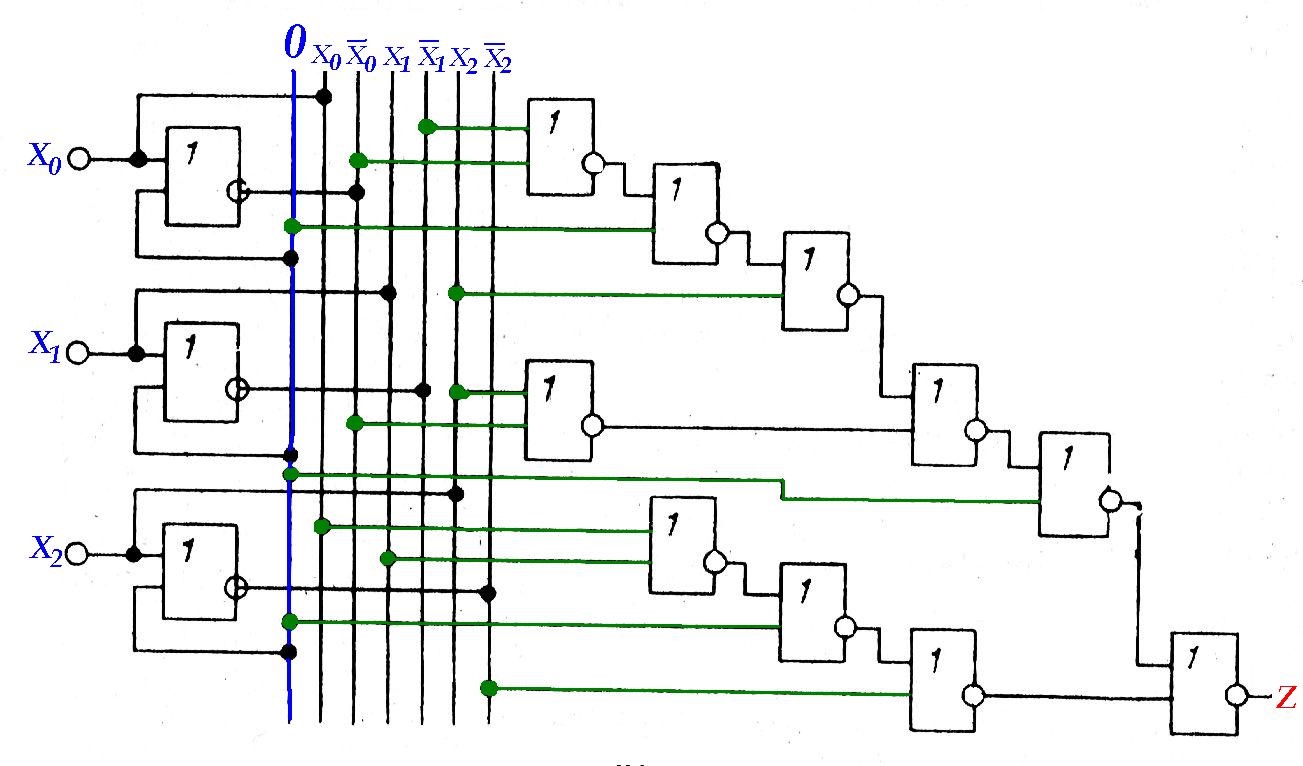
b) MDNN sisaldab ühiseid loogikavahelduvaid.

→ ühised mõnedele elementaarsetele korrutistele vahelduvad võib esitada nagu ühised kordajad ja tõsta sulgude ette.

K.T.Nr.4

Realiseerida LF 2NING-EI LE baasil.