Вивчення коливань зв’язаних маятників

Мета роботи:	Вивчити коливання системи з двох зв’язаних однакових маятників, що мають тільки два ступені вільності.
Прилади і матеріали:	Прилад для вивчення коливань зв’язаних маятників, який складають (два маятника, з’єднувальні пружини, секундомір, лічильник коливань, транспортир).

Теоретичні відомості

Два маятники, що зв’язані між собою пружиною є найпростішим прикладом зв’язаної системи.

Кожен вільний маятник володіє двома ступенями вільності, тобто для опису його руху потрібні два параметри – кути зміщення у двох взаємно перпендикулярних площинах.

Система з двох маятників описується чотирма параметрами і має чотири ступені вільності. Якщо коливання, що відповідають кожному зі ступенів вільності, незалежні, тоді задача опису руху системи є чисто кінематичною, тобто задачею розкладання складного руху на суму більш простих рухів. Якщо між рухами по різним ступеням існує динамічний зв’язок, при якому рух у одному ступені вільності визиває динамічні зміни у всіх інших ступенях вільності, тоді це призводить до обміну коливальною енергією між ступенями вільності, що призводить до фізичних явищ, які відсутні у незалежної системи.

У даній лабораторній роботі вивчають коливання системи з двох зв’язаних однакових маятників, що мають два ступені вільності. Для цього підвіс кожного маятника виконано за допомогою невеликих підшипників з малим тертям, які дозволяють маятникам рухатися тільки у вертикальній площині (дивись рис.1).

Як відомо, для вільного маятника рівняння моментів буде:

(1)

Розклавши sinα в ряд Тейлора і обмежившись лінійним членом, враховуючи що , отримаємо рівняння гармонічного осцилятора

або (2)

де .

У випадку зв’язаних маятників на кожен маятник буде діяти додаткова сила з боку пружини F_зов., яку при невеликих відхиленнях маятників (кут α≈5-7^о) можна розрахувати з закону Гука . Ця сила задає додатковий момент, який слід враховувати, і тоді замість (2) отримаємо для першого і другого маятників, відповідно:

, (3)

(4)

З рівнянь (3) і (4) отримаємо

, (5)

. (6)

Додаючи і віднімаючи (5) і (6) і ввівши позначення і , отримаємо

, (7)

, (8)

де і .

Рівняння (7) і (8) є рівняннями гармонічного осцилятора, і їх розв’язком буде

, (9)

, (10)

де А₀, В₀, і визначаються з початкових умов при і будуть дорівнювати

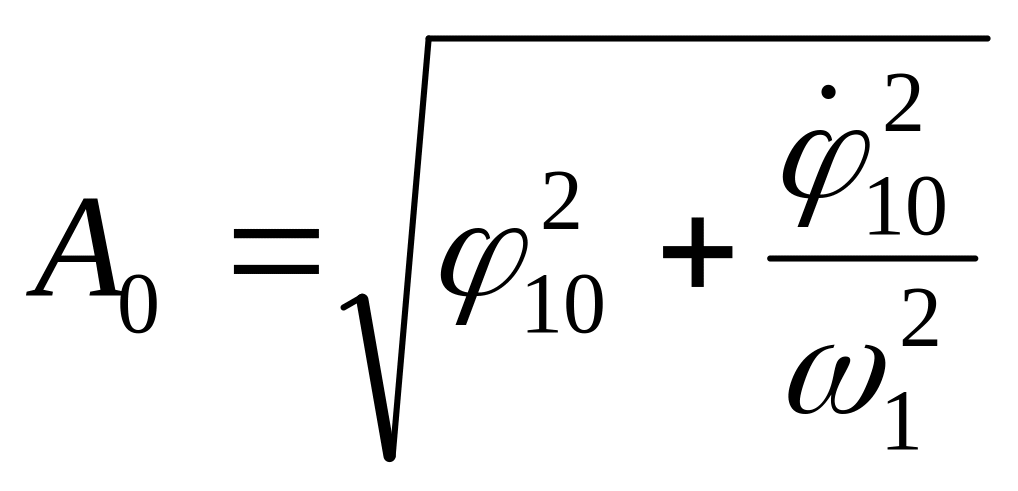; ; (11)

; . (12)

Повертаючись до попередніх координат і і роблячи перетворення зворотні тим, при яких були отримані (7) і (8), отримаємо

, (13)

. (14)

Таким чином, коливання кожного маятника можна описати за допомогою суперпозиції двох гармонічних коливань і , які отримали назву нормальних коливань.

Амплітуди А і В і фази і визначаються з початкових умов (t=0) і будуть дорівнювати

, (15)

, (16)

; . (17)

Розглянемо конкретні випадки.

А. Нехай у початковий момент часу t=0 обидва маятники відхилені від положення рівноваги в одну сторону на рівний кут . Тоді з початкових умов отримаємо ; і відповідно ,

, . (18)

Обидва маятники синхронно коливаються з першою нормальною частотою . (19)

Дійсно, у цьому випадку пружина зв’язку не розтягується і не впливає на рух кожного маятника.

Б. Обидва маятники відхилені на рівний початковий кут , але в протилежних напрямках від положень рівноваги (при t=0). Тоді ; і ,

, . (20)