2.3. Перевод чисел в позиционных системах
Перевод восьмеричных и шестнадцатеричных чисел в двоичную систему очень прост: достаточно каждую цифру заменить эквивалентной ей двоичной триадой (тройкой цифр) или тетрадой (четверкой цифр). |
восьмеричная |
шестнадцатеричная |
2n |
||
цифра |
двоичный код |
цифра |
двоичный код |
|
1 |
001 |
1 |
0001 |
20 =1 |
2 |
010 |
2 |
0010 |
21 =2 |
3 |
011 |
3 |
0011 |
22 =4 |
4 |
100 |
4 |
0100 |
23 =8 |
5 |
101 |
5 |
0101 |
24 =16 |
6 |
110 |
6 |
0110 |
25 =32 |
7 |
111 |
7 |
0111 |
26 =64 |
|
8 |
1000 |
27 =128 |
|
9 |
1001 |
28 =256 |
||
A |
1010 |
29 =512 |
||
B |
1011 |
210 =1024 |
||
C |
1100 |
211 =2048 |
||
D |
1101 |
|
||
E |
1110 |
|||
F |
1111 |
|||
Например:
Чтобы перевести число из двоичной системы в восьмеричную или шестнадцатеричную, его нужно разбить влево и вправо от запятой на триады (для восьмеричной) или тетрады (для шестнадцатеричной) и каждую такую группу заменить соответствующей восьмеричной (шестнадцатеричной) цифрой. |
Например,
(43, 372)8=(1000111,011111010)2
(110101,111010001)2=(65,721)8
(10001110,10101)2 =(216,52)8
Как перевести целое число из десятичной системы в любую другую позиционную систему счисления?
При переводе целого десятичного числа в систему с основанием q его необходимо последовательно делить на q до тех пор, пока не останется остаток, меньший или равный q-1. Число в системе с основанием q записывается как последовательность остатков от деления, записанных в обратном порядке, начиная с последнего. |
Пример: Перевести число 75 из десятичной системы в двоичную, восьмеричную и шестнадцатеричную:
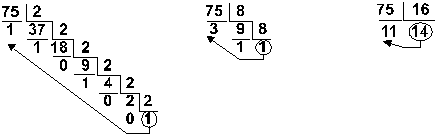
Ответ: 7510 = 1 001 0112 = 1138 = 4B16.
Как перевести правильную десятичную дробь в любую другую позиционную систему счисления?
Пpи переводе правильной десятичной дpоби в систему счисления с основанием q необходимо сначала саму дробь, а затем дробные части всех последующих произведений последовательно умножать на q, отделяя после каждого умножения целую часть пpоизведения. Число в новой системе счисления записывается как последовательность полученных целых частей пpоизведения. |
Умножение пpоизводится до тех поp, пока дpобная часть пpоизведения не станет pавной нулю. Это значит, что сделан точный пеpевод. В пpотивном случае пеpевод осуществляется до заданной точности. Достаточно того количества цифp в pезультате, котоpое поместится в ячейку.
Пример: Перевести число 0,35 из десятичной системы в двоичную, восьмеричную и шестнадцатеричную
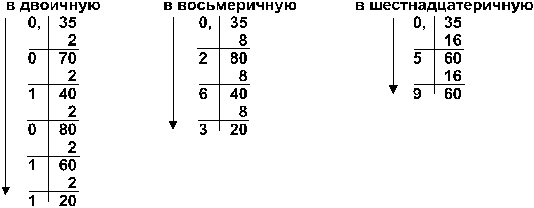
Ответ: 0,3510 = 0,010112 = 0,2638 = 0,5916 .
Как пеpевести число из двоичной (восьмеpичной, шестнадцатеpичной) системы в десятичную?
При переводе числа из двоичной (восьмеричной, шестнадцатеричной) системы в десятичную надо это число представить в виде суммы степеней основания его системы счисления. |