
- •2. Конвективный теплообмен
- •2.1. Схема в.Нуссельта
- •2.2. Основные положения теории подобия и физического моделирования
- •2.2.2. Достаточные условия для подобия вынужденных течений
- •2.2.3. Достаточные условия для подобия свободных термических
- •2.2.4. Достаточные условия для подобия распределений скорости
- •2.2.5. Достаточные условия для подобия температурных полей
- •2.2.6. Необходимые и достаточные условия подобия физических
2.2.2. Достаточные условия для подобия вынужденных течений
Они устанавливаются, основываясь на следующих рассуждениях.
На движущуюся вынужденно жидкость
(газ), находящуюся в элементе пространства
«натуры» или «модели», действуют сила
тяжести
![]() ,
сила вязкостного трения
,
сила вязкостного трения![]() и сила
и сила![]() ,
связанная с наличием градиента давления
вдоль потока. Векторная сумма этих сил
является равнодействующей, а ее значение,
взятое с противоположным знаком,
называется силой инерции
,
связанная с наличием градиента давления
вдоль потока. Векторная сумма этих сил
является равнодействующей, а ее значение,
взятое с противоположным знаком,
называется силой инерции![]() .
.
Согласно принципу Даламбера имеем для выделенного элемента пространства соотношение
![]() ,
(2.6)
,
(2.6)
представляющее собой уравнение Навье–Стокса, записанное в векторах сил, действующих на движущуюся среду.
В безразмерной форме получаем вместо (2.6)
![]() (2.6)
(2.6)
Ясно, что если в каждой паре сходственным образом расположенных точек пространства «натуры» и «модели» одноименные слагаемые левой части (2.6) совпадают друг с другом, то при выполнении необходимых условий этого достаточно, чтобы утверждать о подобии «натурного» и «модельного» течений, так как уравнения движения в форме (2.6) и условия однозначности их решения становятся одинаковыми для «натуры» и «модели».
В теории подобия доказывается, что достаточно сравнивать между собой не сами отношения указанных сил, а их меры.
Для вынужденного обтекания потоком
пластины или при его течении в прямолинейном
канале постоянного поперечного сечения
влияние градиента давления отсутствует
или незначительно и развитие процесса
(формирование распределения скорости)
определяется отношением силы инерции
![]() к силе вязкостного трения
к силе вязкостного трения![]() .
.
Вычислим меру отношения этих сил для
частного случая стационарного течения
среды с постоянными физическими
свойствами. В этом случае силы
![]() и
и![]() ,
действующие на жидкость или газ,
находящиеся в единице объема, таковы:
,
действующие на жидкость или газ,
находящиеся в единице объема, таковы:
![]() (2.7)
(2.7)
Надо помнить, что операторы
![]() gradи
gradи![]() действуют не на вектор
действуют не на вектор![]() ,
а на его проекцию
,
а на его проекцию![]() на осиx,yиzсоответственно.
на осиx,yиzсоответственно.
В формуле (2.7) и- это соответственно плотность жидкости
(газа) и коэффициент динамической
вязкости, а оператор (![]() grad)
таков:
grad)
таков:
![]()
Мера отношения
![]() обозначается как
обозначается как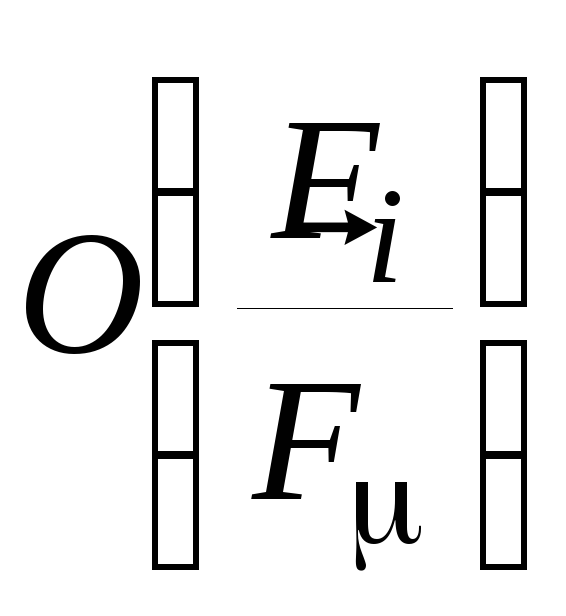 (O– первая буква
латинского словаOrdo(порядок)).
(O– первая буква
латинского словаOrdo(порядок)).
Итак, имеем
 (2.8)
(2.8)
В теории подобия показывается, что в
качестве меры искомой величины fназначается какое-либо известное при
постановке задачи ее характерное
значениеf0,
важное для развития явления. В качестве
меры производных![]() ...назначаются отношения
...назначаются отношения![]() и т.д., гдеx0- характерное известное значение
аргументаx. Меры
обязательно назначаются одинаковым
образом для «натуры» и «модели». Меры
для известных величин - в частности,
свойств среды - не назначаются: они
выбираются из справочного материала
по важной для исследуемого процесса
(характерной) переменной, например, по
характерной температуре и др.
и т.д., гдеx0- характерное известное значение
аргументаx. Меры
обязательно назначаются одинаковым
образом для «натуры» и «модели». Меры
для известных величин - в частности,
свойств среды - не назначаются: они
выбираются из справочного материала
по важной для исследуемого процесса
(характерной) переменной, например, по
характерной температуре и др.
Назначим в качестве меры для
![]() известную скорость потокаw0на входе в трубу, а в качестве меры для
протяженностейx,y,z- ее диаметрd.
известную скорость потокаw0на входе в трубу, а в качестве меры для
протяженностейx,y,z- ее диаметрd.
Тогда имеем вместо (2.8)
![]() . (2.9)
. (2.9)
Безразмерный комплекс в правой части (2.9) является мерой отношения силы инерции к силе вязкостного трения, его величина определяет характер вынужденного течения жидкости (газа). Он называется критерием Рейнольдса и обозначается Re (Reynolds):
![]() или
или![]()
где =/- коэффициент кинематической вязкости.
Итак, для подобия распределения скоростей в двух безградиентных вынужденных течениях в каналах достаточно, чтобы выполнялось равенство критериев Рейнольдса, составленных для «натуры» и «модели»:
![]() или
или![]() (2.10)
(2.10)
Если обозначить характерный для потока размер через l0(в рассматриваемом случаеl0d), то достаточное условие подобия двух вынужденных течений (2.10) принимает более общий вид
![]() (2.10)
(2.10)
