Лабораторная работа 1 Неравномерные коды Шеннона – Фано и Хаффмана

При построении оптимальных кодов наибольшее распространение нашли методики Шеннона – Фано и Хаффмана.

Согласно методике Шеннона – Фано построение оптимального кода ансамбля из сообщений сводится к следующему:

1-й шаг. Множество из сообщений располагается в порядке убывания вероятностей.

2-й шаг. Первоначальный ансамбль кодируемых сигналов разбивается на две группы таким образом, чтобы суммарные вероятности сообщений обеих групп были по возможности равны. Если равной вероятности в подгруппах нельзя достичь, то их делят тик, чтобы в верхней части (верхней подгруппе) оставались символы, суммарная вероятность которых меньше суммарной вероятности символов в нижней части (в нижней подгруппе).

3-й шаг. Первой группе присваивается символ 0, второй группе – символ 1.

4-й шаг. Каждую из образованных подгрупп делят на две части таким образом, чтобы суммарные вероятности вновь образованных подгрупп были по возможности равны.

5-й шаг. Первым группам каждой из подгрупп вновь присваивается 0, а вторым – 1. Таким образом, мы получаем вторые цифры кода. Затем каждая из четырех групп вновь делится на равные (с точки зрения суммарной вероятности) части до тех пор, пока в каждой из подгрупп не останется по одной букве.

Кодирование Хаффмана.

Кодирование Хаффмана производится за три шага. Мы наглядно поясним этот процесс на маленьком примере.

1. Упорядочение. Расположить знаки в порядке убывания их вероятностей.

2. Редукция. Объединить два знака с наименьшими вероятностями в один составной знак. Переупорядочить список знаков в соответствии с шагом 1. Продолжать этот процесс до тех пор, пока все знаки не будут объединены.

3. Кодирование. Начать с последнего объединения. Приписать пер­вой компоненте составного знака символ «О», а второй - символ «1». Продолжать этот процесс до тех пор, пока все простые знаки не будут закодированы.

В случае, когда несколько знаков имеют одинаковые вероятности, объединяются те два из них, которые до этого имели наименьшее число объединений. Этим достигается выравнивание длин кодовых слов, что облегчает передачу информации.

Пример 1. Построить оптимальный код сообщения, состоящего из 8 равновероятных букв.

Решение. Так как вероятности данного ансамбля сообщений равны и порядок их размещения не играет роли, то располагаем сообщения в порядке возрастания порядковых номеров. Затем разбиваем данное множество сообщений на две равновероятные группы. Первой группе в качестве первого символа кодовых слов присваиваем. 0, второй группе – 1. В колонке «кодовые слова» записываем 4 нуля и 4 единицы. После этого согласно методике Шеннона–Фано, разбиваем каждую из подгрупп еще на две равновероятные подгруппы. Затем каждой первой подгруппе в качестве второго символа присваиваем 0, а второй –1 и записы­ваем в колонку «кодовые слова». Далее каждую из четырех, подгрупп разбиваем на две равновероятные части и первой из них присваиваем 0, а второй –1, таким образом, в колонке «кодовые слова» появятся значения третьего символа кодовых слов.

Для исходного алфавита оптимальный код будет иметь вид: A₁ = 000; A₂ = 001; A₃ = 010; A₄ = 011; A₅ = 100; A₆ = 101; A₇ = 110; A₈ = 111.

Проверка.

бит/символ,

,

L_cp = H – код оптимальный.

Примечание. Для ансамблей равновероятных сообщений оптимальным всегда будет равномерный код.

Пример 2. Построить оптимальный код сообщения, в котором вероятности появления букв первичного алфавита, состоящего из 8 символов, являются целой отрицательной степенью двух, a .

Решение. Построение оптимального кода ведется по методике Шеннона–Фано. Результат построения отражен в таблице:

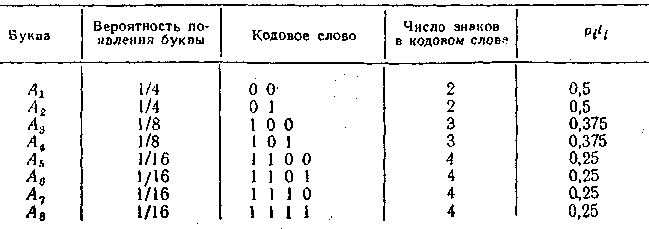
Проверка.

;

Примечание. Кодовые слова одинаковой вероятности появления имеют равную длину.

Пример 3. Построить ОНК для передачи сообщений, в которых вероятности появления букв первичного алфавита равны: A₁ = 0.5; A₂ = 0.25; A₃ = 0.098; A₄ = 0.052; A₅ = 0.04; A₆ = 0.03; A₇ = 0.019; A₈ = 0.011. Определить коэффициент статистического сжатия и коэффициент относительной эффективности.

Решение. Построение ведется по методике Шеннона–Фано. Результаты построения отражены в таблице:

.

.