
- •1. Матрицы. Определители. Системы линейных уравнений
- •1.1. Матрицы. Действия с матрицами
- •1.2. Свойства действий с матрицами
- •1.3. Определители. Свойства определителей
- •1.4. Обратная матрица
- •1.5. Ранг матрицы
- •1.6. Системы линейных уравнений
- •1.7. Правило Крамера
- •1.8. Метод Гаусса
- •1.9. Теорема Кронекера-Капелли
- •2. Векторы на плоскости
- •2.1. Векторы, линейные операции над векторами
- •2.4. Скалярное произведение векторов, его свойства
- •3. Прямая линия на плоскости
- •4. Кривые второго порядка
- •5. Введение в анализ
- •5.1. Предел функции. Бесконечно малая и бесконечно большая функции
- •5.2. Теоремы о пределах
- •Постоянный множитель можно выносить за знак предела:
- •5.3. Раскрытие неопределенностей. Замечательные пределы
- •6. Производная и дифференциал
- •6.1. Производная функции
- •6.2. Производная сложной функции
- •6.3. Производные высших порядков
- •6.4. Дифференциалы функции
- •6.7. Выпуклость, вогнутость кривой. Точки перегиба
- •6.8. Асимптоты графика функции
- •6.9. Полная схема исследования функции
- •7. Задачи для контрольной работы
- •8. Образец выполнения контрольной работы
- •Из этой системы обратным ходом метода Гаусса находим
- •9. Вопросы для экзамена
- •Список литературы
- •Оглавление
- •1. Матрицы. Определители. Системы
- •1.1. Матрицы. Действия с матрицами 3
5. Введение в анализ
Если каждому
элементу x![]() X
ставится в соответствие определенный
элемент y
Y
по какому-либо закону, то говорят, что
на множестве Х задана функция
у = f
(x).
X
ставится в соответствие определенный
элемент y
Y
по какому-либо закону, то говорят, что
на множестве Х задана функция
у = f
(x).
Множество Х называется областью определения функции, а множество Y – областью её значений.
Существуют следующие способы задания функции: табличный, графический, аналитический, словесный.
Элементарные функции делятся на алгебраические и неалгебраические (трансцендентные). К алгебраическим относятся: целая рациональная, дробно-рациональная и иррациональная функции.
5.1. Предел функции. Бесконечно малая и бесконечно большая функции
Число А называется
пределом
функции
f(x)
при х стремящемся к х0,
если для любого положительного числа
ε > 0 найдется такое положительное
число
>0, что для всех х, удовлетворяющих
условию 0<![]() < ,
выполняется неравенство
< ,
выполняется неравенство
![]() <
ε .
<
ε .
Записывают
![]() =
А.
=
А.
Если при хх0
х принимает
значения меньшие (большие) х0
и при этом функция f
(x)
стремится к некоторому числу А1
(А2),
то А1
(А2)
называют односторонним
пределом
функции f
(x)
слева (справа) и записывают
![]() = А1,
(
= А1,
(![]() = А2).
= А2).
Если А1 А2, то не существует.
Если
=
![]() = А, то
= А.
= А, то
= А.
Функция (х)
называется бесконечно
малой
величиной
при хх0,
если её предел равен 0:
![]() =
0.
=
0.
Свойства бесконечно малых величин
Алгебраическая сумма конечного числа бесконечно малых величин есть величина бесконечно малая.
Произведение двух бесконечно малых есть величина бесконечно малая.
Произведение бесконечно малой величины на ограниченную функцию есть величина бесконечно малая.
Функция f(х) называется бесконечно большой величиной при хх0, если = .
Теорема.
Если функция (х)
бесконечно малая величина при хх0,
то функция
f(x) =![]() является
бесконечно большой при хх0.
И обратно, если f(х)
бесконечно большая при хх
является
бесконечно большой при хх0.
И обратно, если f(х)
бесконечно большая при хх![]() ,
то (х)
=
,
то (х)
=![]() вели-
чина
бесконечно малая при хх
.
вели-
чина
бесконечно малая при хх
.
Пример.
Найти
![]() .
.
При х2 функция (х–2) бесконечно малая, тогда = .
5.2. Теоремы о пределах
Если существуют
пределы
![]() =
А и
=
А и
![]() =
В, то имеют место теоремы:
=
В, то имеют место теоремы:
1. Предел постоянной равен этой постоянной:
![]() =
С.
=
С.
2. Предел суммы конечного числа функций равен сумме пределов этих функций:
![]() =
+
.
=
+
.
3. Предел произведения конечного числа функций равен произведению пределов этих функций:
![]() =
×
.
=
×
.
Постоянный множитель можно выносить за знак предела:
![]() .
.
4. Предел частного
двух функций равен частному пределов
этих функций при условии, что
![]() ≠0:
≠0:
![]() =
=
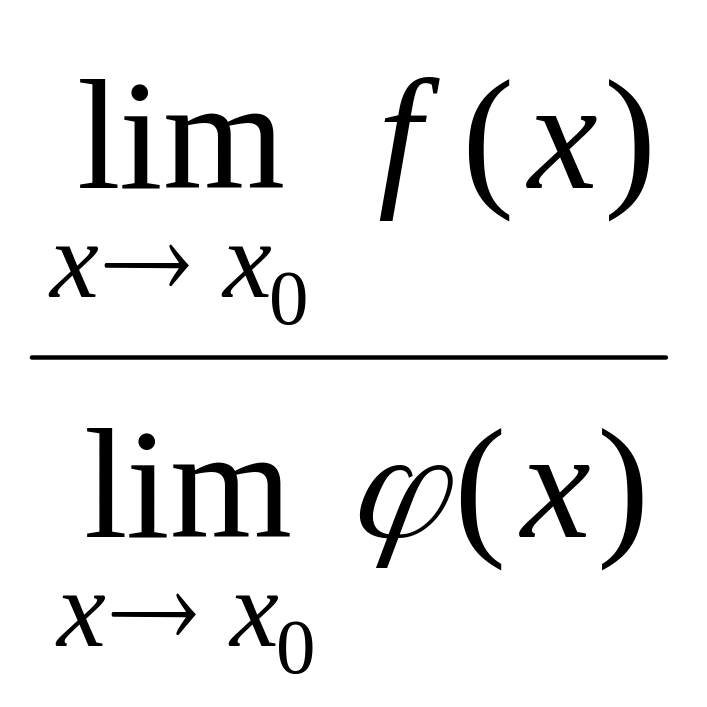 .
.
5.3. Раскрытие неопределенностей. Замечательные пределы
К неопределенностям
относятся выражения вида:
![]() ,
,
![]() ,
,
0×,
0,
1,
00,
которые появляются при подстановке
предельного значения переменной.
Нахождение предела функций в таких
случаях называют раскрытием
неопределенностей.
,
,
0×,
0,
1,
00,
которые появляются при подстановке
предельного значения переменной.
Нахождение предела функций в таких
случаях называют раскрытием
неопределенностей.
Пример.
Найти: 1)
![]() ;
2)
;
2)
![]() ;
3)
;
3)
![]() .
.
Имеем неопределенности
вида
![]() ,
разделим числитель и знаменатель на х
с наибольшим
показателем степени числителя и
знаменателя.
,
разделим числитель и знаменатель на х
с наибольшим
показателем степени числителя и
знаменателя.
1)![]() =
=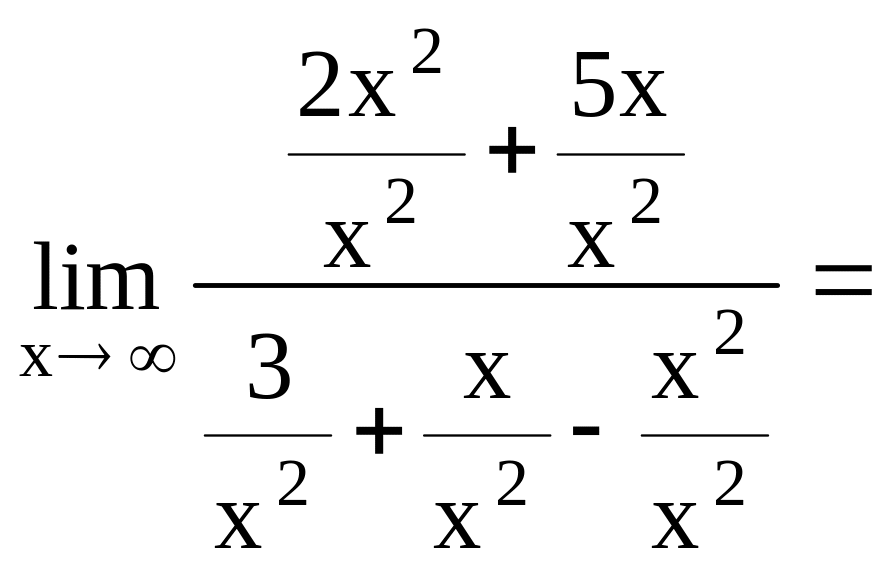
=![]()
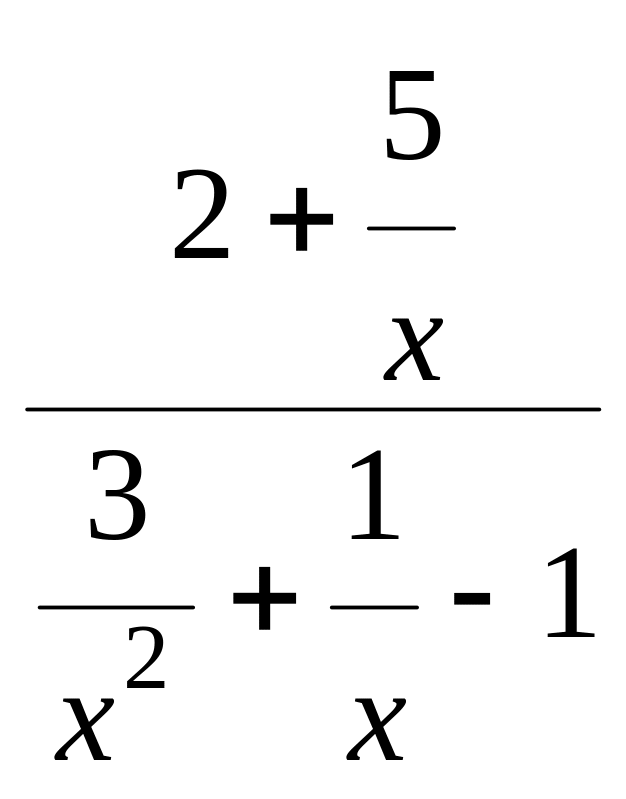 = (
= (![]() +
+
![]() )
(
)
(![]() )
= =
)
= =![]() =
2.
=
2.
2)
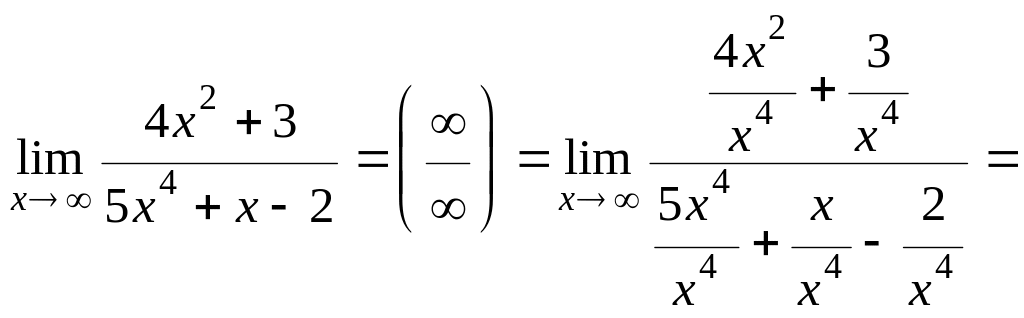
=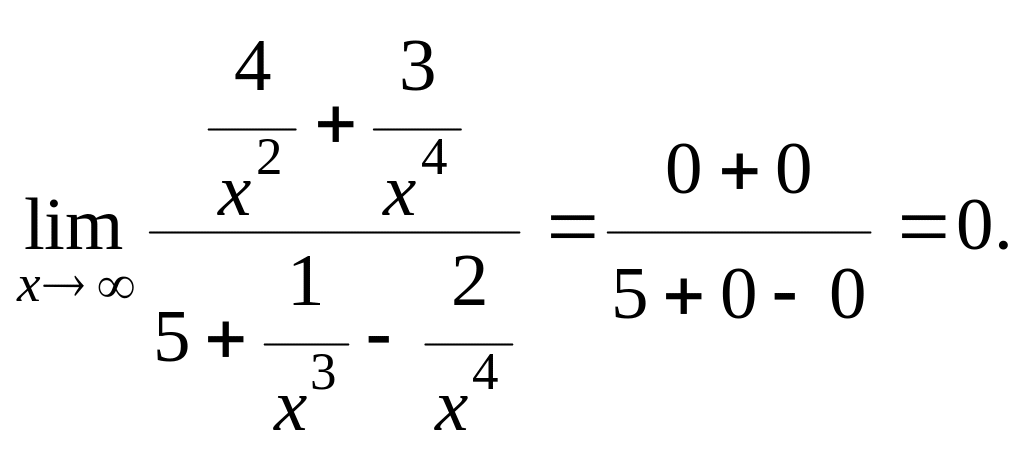
3)
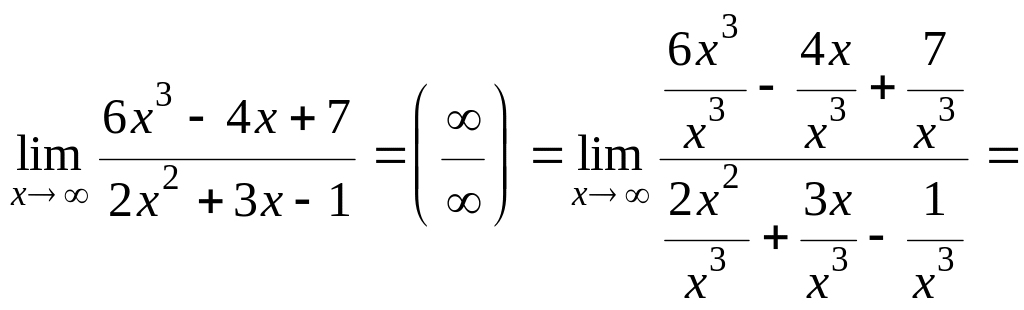
=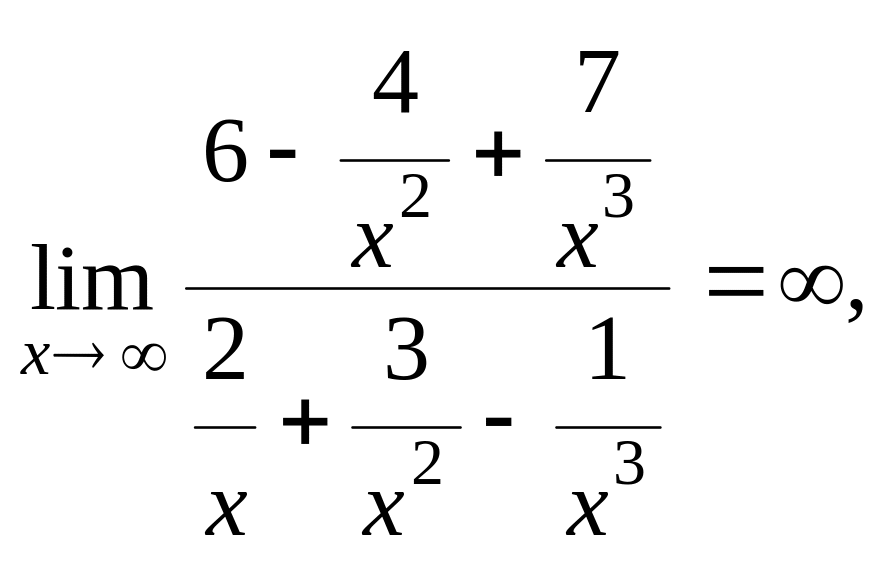
так
как знаменатель дроби
![]() является бесконечно малой величиной
при
является бесконечно малой величиной
при
![]() ,
тогда
,
тогда
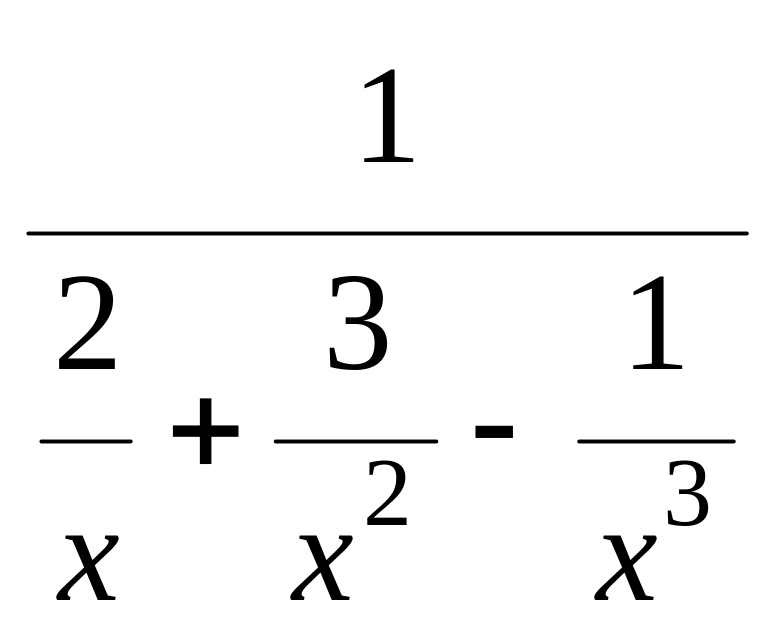 является бесконечно большой величиной;
числитель дроби
является бесконечно большой величиной;
числитель дроби
![]() является функцией, предел которой равен
6 при
,
функция под знаком предела является
бесконечно большой величиной, искомый
предел равен
является функцией, предел которой равен
6 при
,
функция под знаком предела является
бесконечно большой величиной, искомый
предел равен
![]() .
.
Пример.
![]() .
.
Подставим предельное значение х = 2, получим неопределенность . Для раскрытия этой неопределенности разложим числитель и знаменатель дроби на множители.
![]() =
=
![]()
![]() =
=
![]() =
=
![]() .
.
Пример.
![]()
Имеем неопределенность вида ( – ). Приведем дроби к общему знаменателю.
![]() ,
т.к. знаменатель дроби (
,
т.к. знаменатель дроби (![]() )
при
)
при
![]() является бесконечно малой величиной,
тогда
является бесконечно малой величиной,
тогда
![]() – бесконечно большая величина; числитель
дроби (
– бесконечно большая величина; числитель
дроби (![]() )
является функцией, предел которой при
равен –5, функция
)
является функцией, предел которой при
равен –5, функция
![]() является бесконечно большой величиной
при
,
предел равен
.
является бесконечно большой величиной
при
,
предел равен
.
Первым замечательным
пределом
называется
![]()
![]() =
1.
=
1.
Вторым замечательным пределом называется:
![]() =
=![]() (1+y)
(1+y)![]() =
e.
=
e.
Пример.
![]() .
.
При х0
имеем неопределенность
![]() ,
воспользуемся первым замечательным
пределом, умножим и разделим дробь на
число 3.
,
воспользуемся первым замечательным
пределом, умножим и разделим дробь на
число 3.
=
![]() =
=
![]()
![]() =
=
![]() 1
=
.
1
=
.
Пример.
![]() .
.
Имеем неопределенность 1. Воспользуемся вторым замечательным пределом.
=![]() =
=![]() =
e2.
=
e2.
5.4. Непрерывность функции
Функция f(х) называется непрерывной в точке х0 , если:
она определена в этой точке и в ее окрестности;
имеет конечный предел при
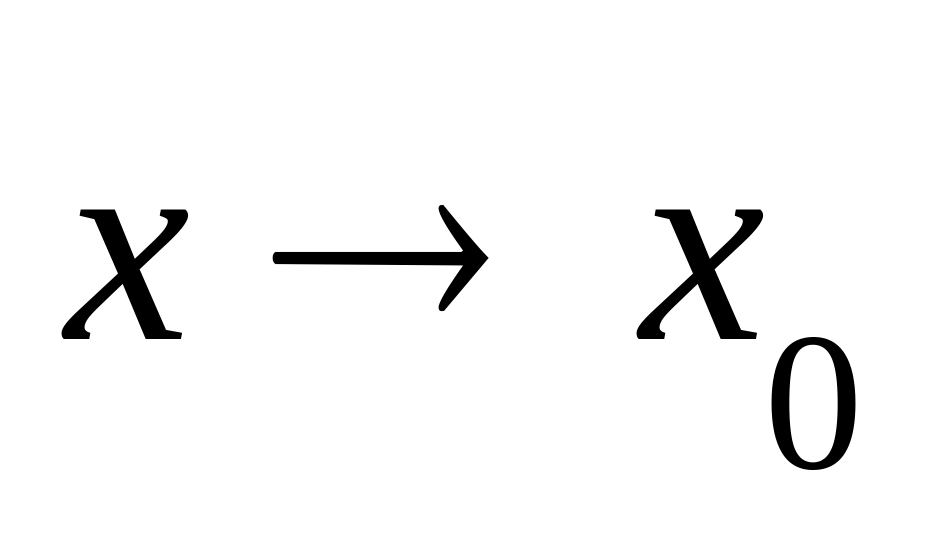 ;
;этот предел равен значению функции в точке х0 , то есть
![]() f (x)
= f (x0
).
f (x)
= f (x0
).
Для непрерывной функции возможна перестановка символов предела и функции f (x) = f ( х ).
Если хотя бы одно из этих условий не выполняется, то функция называется разрывной в точке х0, а сама точка х0 называется точкой разрыва функции.
Если существуют
односторонние пределы, но не равны между
собой,
![]() f(x)
≠
f(x)
≠
![]() f(x),
то х0
– точка разрыва первого рода.
f(x),
то х0
– точка разрыва первого рода.
Если хотя бы один из односторонних пределов не существует (), то х0 – точка разрыва второго рода.
Сумма, произведение, частное непрерывных функций есть непрерывная функция.
Пример.
Исследовать на
непрерывность функцию
![]()
Функция задана различными аналитическими выражениями на интервалах (, 0) и [ 0, ). Исследуем точку х = 0, найдем односторонние пределы:
![]() f(x)
=
f(x)
=
![]() = 2,
= 2,
![]() f(x)
=
x
f(x)
=
x![]() = 0.
= 0.
Односторонние пределы существуют, но не равны, поэтому х = 0 – точка разрыва первого рода.
Примеры для самостоятельной работы
1. Вычислить:
а)
![]() ; б)
; б)
![]() ;
;
в)
![]()
![]() ; г)
; г)
![]() ;
;
д)
![]() ; е)
(1+2х
)
; е)
(1+2х
)![]() ; ж)
; ж)
![]() .
.
2. Исследовать на непрерывность функции:
а)
![]() б)
б)
![]() .
.
