1.8. Метод Гаусса

Метод Гаусса – метод последовательного исключения переменных – заключается в том, что с помощью элементарных преобразований система уравнений приводится к равносильной системе ступенчатого (или треугольного) вида, из которой последовательно, начиная с последних (по номеру) переменных, находятся все остальные переменные.

Элементарные преобразования системы уравнений состоят в выполнении следующих действий:

1. перестановка местами двух уравнений;

2. умножение обеих частей какого-либо уравнения на число λ ≠ 0;

3. прибавление к одному уравнению системы другого уравнения, умноженного на число.

Пример. Решить систему уравнений методом Гаусса:

Исключим переменную x из 2-го и 3-го уравнений системы. Умножим первое уравнение на (-2) и прибавим ко 2-му уравнению, затем умножим 1-е уравнение на (-1) и прибавим к 3-му уравнению системы. Получим систему уравнений

Разделим 2-е уравнение на (-3) и получим систему уравнений

Исключим переменную y из 3-го уравнения системы, для этого умножим 2-е уравнение на 2 и прибавим к 3-му уравнению, получим систему уравнений

Выразим переменную z из 3-го уравнения, y – из 2-го уравнения, переменную х из 1-го уравнения

Имеем x=1, y=2, z=3 – единственное решение системы.

Пример. Решить систему уравнений методом Гаусса:

Умножим 1-е уравнение на (-2) и прибавим ко 2-му уравнению, затем прибавим 1-е уравнение к 3-му уравнению. Получим систему уравнений:

Далее умножим 2-е уравнение на 2 и прибавим к 3-му уравнению:

В полученной системе имеем противоречие 0 = 6, значит, исходная система несовместна.

Пример. Решить систему уравнений методом Гаусса

Исключим переменную x₁ из 2-го , 3-го и 4-го уравнений системы. Умножим 1-е уравнение на (-2) и прибавим ко 2-му и 3-му уравнениям, умножим 1-е уравнение на (-3) и прибавим к 4-му уравнению. Получим систему уравнений

Исключим переменную x₂ из 3-го и 4-го уравнений системы. Умножим 2-е уравнение на и прибавим к 3-му и 4-му уравнениям. Получим систему уравнений

Исключим переменную х₃ из 4-го уравнения системы. Для этого умножим 3-е уравнение на (-1) и прибавим к 4-му уравнению системы. После удаления последнего уравнения система уравнений примет вид

Из этой системы обратным ходом метода Гаусса находим

Так как х₄ может принимать любые значения, то система имеет бесконечное множество решений.

Примеры для самостоятельной работы

Решить следующие системы линейных уравнений:

1. 2.

3. 4.

5. 6.

1.9. Теорема Кронекера-Капелли

Теорема Кронекера-Капелли. Система линейных уравнений совместна тогда и только тогда, когда ранг матрицы системы равен рангу расширенной матрицы этой системы.

Теорема. Если ранг совместной системы равен числу неизвестных, то система имеет единственное решение.

Теорема. Если ранг совместной системы меньше числа неизвестных, то система имеет бесконечное множество решений.

2. Векторы на плоскости

2.1. Векторы, линейные операции над векторами

В ектором называется направленный отрезок, где А начальная, а В – конечная точки вектора.

Векторы обозначают также малыми латинскими буквами , , .

Модуль вектора - это длина отрезка, изображающего вектор, записывают .

Единичным вектором называется вектор, длина которого равна единице.

Нулевым вектором называется вектор, модуль которого равен единице, а направление не определено.

Два вектора называются равными, если равны их модули и совпадают направления.

Векторы, лежащие на одной прямой или параллельных прямых, называются коллинеарными, записывают  .

Векторы, противоположно направленные и имеющие равные длины, называются противоположными. Вектор, противоположный вектору , обозначается через .

С уммой двух векторов и называется вектор , начало которого совпадает с началом вектора , а конец - с концом вектора при условии, что начало вектора совпадает с концом вектора (правило треугольников).

Вектор суммы равен диагонали параллелограмма, построенного на векторах и как на сторонах и выходящий из их общего начала (правило параллелограмма).

Разностью двух векторов и называется вектор , который в сумме с вектором дает вектор . Начало вектора совпадает с концом вычитаемого вектора , а конец – с концом уменьшаемого вектора . Разность векторов можно рассматривать как сумму векторов и .

Произведением вектора на число  называется вектор с длиной равной и сонаправленный с вектором , если >0, и с направлением противоположным при <0.

Линейные операции над векторами обладают следующими свойствами:

1) ;

2) ;

3) ;

4) .

Ортом вектора называется сонаправленный с ним единичный вектор . Всякий вектор может быть представлен в виде .

Необходимое и достаточное условие коллинеарности двух векторов и выражается равенством .

Векторы, параллельные одной и той же плоскости (или лежащие в одной плоскости), называются компланарными. Необходимое и достаточное условие компланарности трех векторов , , выражается равенством .

2.2. Проекция вектора на ось. Теоремы о проекциях

Проекцией вектора на ось называется число, равное длине составляющей, взятое со знаком плюс, если составляющая сонаправлена с осью и со знаком минус в противном случае

.

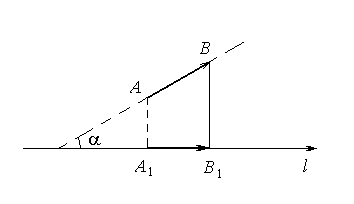
Теорема 1. Проекция вектора на ось равна произведению длины вектора на косинус угла между вектором и осью

.

Теорема 2. Если вектор умножить на число , то его проекция на ось также умножится на это число

.

Теорема 3. Проекция суммы двух векторов на ось равна сумме слагаемых векторов на ту же ось

.

Координатами вектора называют его проекции на координатные оси Ох, Оу, Оz. Записывают или

.

Эта формула называется разложением вектора по ортам координатных осей Ох, Оу, Оz.

Модуль вектора равен квадратному корню из суммы квадратов его проекций на оси координат

.

Направляющими косинусами вектора называются косинусы углов , , , образованных этим вектором с осями координат Ох, Оу, Оz:

; ; ;

.

2.3. Действия над векторами, заданными

своими координатами

Пусть даны векторы и . При сложении векторов их одноименные координаты складываются

или .

При умножении вектора на число все его координаты умножаются на это число

или .

Два вектора и равны тогда и только тогда, когда выполняются равенства

a_х = b_x; a_y = b_y; a_z = b_z .

Необходимым и достаточным условием коллинеарности векторов и является пропорциональность их координат

.

Если известны координаты начала А(х₁, у₁, z₁) и конца В(х₂, у₂, z₂) вектора , то его координаты определяются =(х₂ -х₁, у₂ -у₁, z₂ -z₁).

Длину вектора, заданного координатами начала и конца, вычисляют по формуле

.

Пример. Даны векторы = (1; -3; 2) и = (3; 4; -5). Найти векторы:

; , , .

= ( 1 + 3; 3 + 4; 2 + ( 5)) = ( 4; 1; 3);

= ( 1 3; 3 4; 2  ( 5)) = ( 2; 7; 7);

= 2 ( 1;  3; 2) 3( 3; 4; 5) = (2; 6; 4)  (9; 12; 15) =

= (2  9; 6 12; 4 ( 15)) = ( 7; 18; 19);

= 3 (1; 3; 2) + 4 (3; 4; 5) =

= (3; 9; 6) + (12; 16; 20)=(3 + 12; 9 + 16; 6 + ( 20)) = (15; 7; 14).

Пример. Даны две точки А(9; 7; 4) и В( 1; 3; 1). Найти координаты и длину вектора .

= ( х₂ х₁, у₂ у₁, z₂ z₁) = (1 9; 3( 7); 1 ( 4)) = ( 10; 10; 5);

= =15.

Пример. Дан вектор =( 4; 6; 12). Написать разложение вектора по координатным ортам и найти орт вектора .

Разложение вектора по координатным ортам имеет вид .

Длина вектора .

Орт вектора .

Пример. Определить, при каких  и  векторы и коллинеарны.

Запишем условие коллинеарности векторов: , откуда 3 = 12;  = 4; 2 = 3,  = 3/2.

Пример. Найти длину и направляющие косинусы вектора , если А (4; 2; 1) и В (7; 6; 11).

Найдем координаты вектора = (7  4; 6  2; 11 + 1) = (3; 4; 12).

Модуль вектора ;

; ; .