1.5. Ранг матрицы

Наивысший порядок минора, отличного от нуля, называется рангом матрицы.

Обозначается rang A или r(A), r(A_m×n) ≤ min{m, n}.

При вычислении ранга матрицы следует переходить от миноров меньших порядков к минорам больших порядков. Если найден минор k-го порядка Δ_k, отличный от нуля, то требуется вычислить лишь миноры (k+1)-го порядка, окаймляющие минор Δ_k. Если все они равны нулю, то ранг матрицы равен k.

Пример. Найти ранг матрицы:

Возьмем отличный от нуля минор 2-го порядка

Минор 3-го порядка

окаймляющий минор Δ₂, отличен от нуля. Два минора 4-го порядка, окаймляющие минор Δ₃, равны нулю:

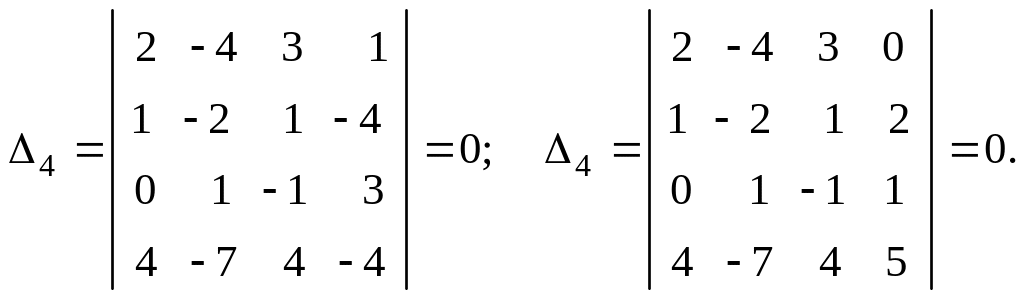
Таким образом, ранг матрицы А равен трем (rangA = 3).

Для облегчения вычисления ранга матрицы используются элементарные преобразования матрицы, сохраняющие ранг матрицы:

1. отбрасывание нулевой строки (столбца);

2. умножение всех элементов строки (столбца) матрицы на число, не равное нулю;

3. изменение порядка строк (столбцов) матрицы;

4. прибавление к каждому элементу одной строки (столбца) соответствующих элементов другой строки (столбца), умноженных на любое число;

5. транспонирование матрицы.

Матрица, полученная из данной элементарными преобразованиями, называется эквивалентной данной, обозначается знаком ~ .

Примеры для самостоятельной работы

Найти ранг матрицы:

1. 3.

1.6. Системы линейных уравнений

Система уравнений вида:

где a_ij – коэффициенты; x_j – переменные; b_i – свободные члены, называется системой линейных уравнений. Решить систему линейных уравнений – значит указать такие наборы значений переменных, которые обращают уравнения системы в тождества. Система линейных уравнений называется:

а) совместной, если она имеет хотя бы одно решение;

б) несовместной, если она не имеет решений;

в) определенной, если она имеет единственное решение;

г) неопределенной, если она имеет более одного решения;

д) однородной, если все b_i = 0;

е) неоднородной, если есть b_i ≠ 0.

Две системы уравнений называются равносильными, или эквивалентными, если они имеют одно и то же множество решений.

1.7. Правило Крамера

Правило Крамера применяется к системам, у которых число уравнений m равно числу переменных n. Рассмотрим систему двух линейных уравнений с двумя переменными:

Вычислим определители

1. Если Δ ≠ 0, то система имеет единственное решение, определяемое по формулам Крамера

.

2. Если Δ = 0, а хотя бы один из определителей Δх или Δy отличен от нуля, то система не имеет решений.

3. Если Δ= Δх = Δy = 0, то система имеет бесконечно много решений.

Пример. Решить систему по правилу Крамера:

Вычислим определители:

Рассмотрим систему трех уравнений с тремя неизвестными:

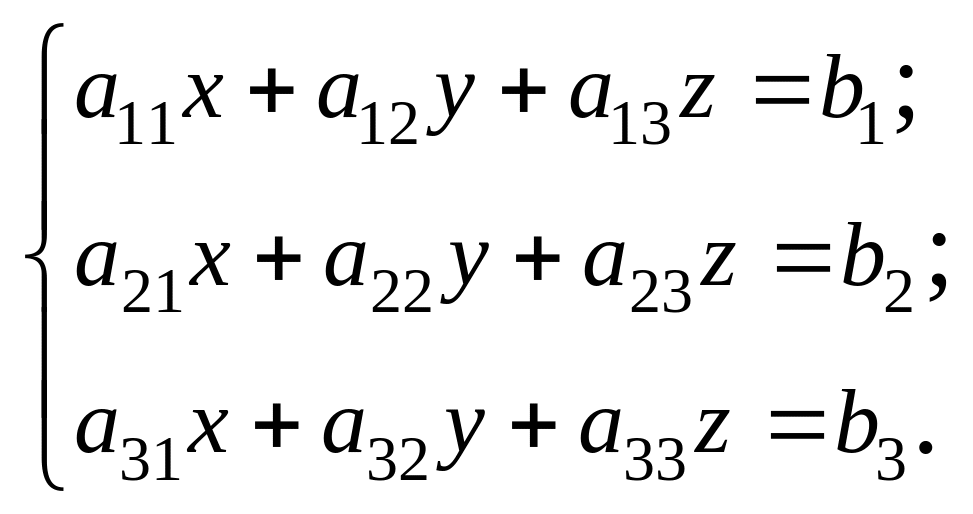
Вычислим определители

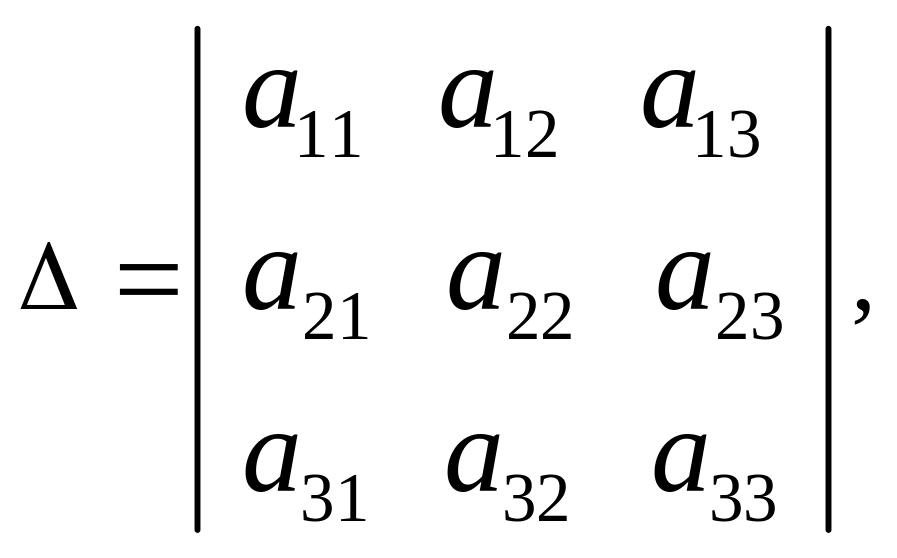
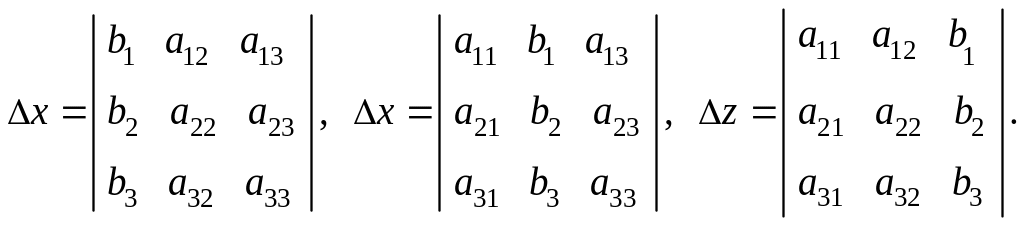
1. Если ∆ ≠ 0, то система имеет единственное решение

, , .

2. Если ∆ = 0, а хотя бы один из определителей ∆x, ∆y, ∆z отличен от нуля, то система не имеет решений.

3. Если ∆ = ∆x = ∆y = ∆z = 0, то возможны случаи:

а) система не имеет решений;

б) система имеет бесконечно много решений.

Пример. Решить систему по правилу Крамера:

Вычислим определители:

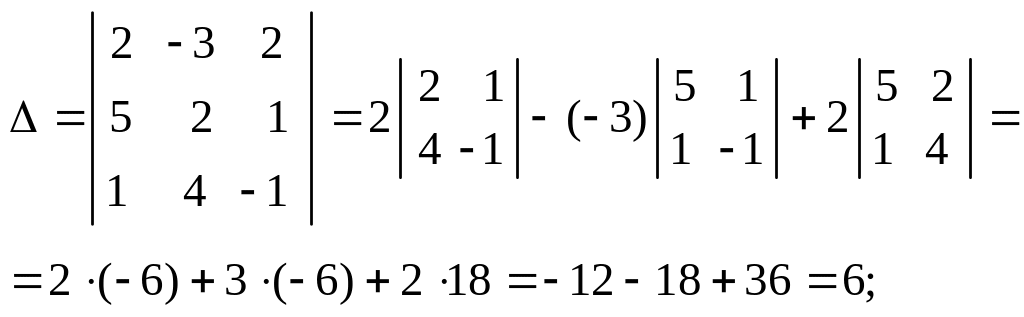
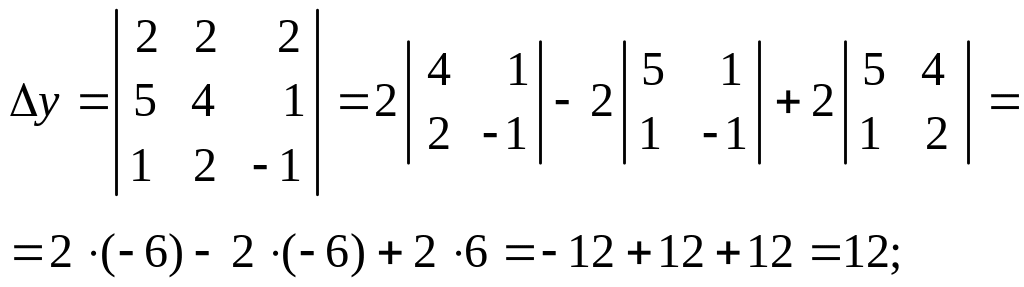
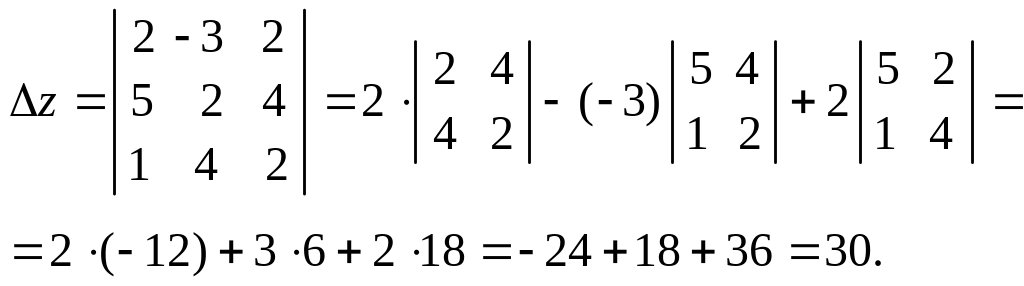
По формулам Крамера

Пример. Решить систему по правилу Крамера:

Вычислим определители:

Система не имеет решений.