Из этой системы обратным ходом метода Гаусса находим

х₄ = 1; х₃ = 5  8х₄ = 5  81 =  3;

х₂ = (5 9х₃  17х₄) = (5 9(3)  171) = 1;

х₁ = 3+2х₂ + 2х₃ + 3х₄ = 3 + 21 + 2(3) + 31 = 2.

Ответ: (2; 1; 3; 1).

Задание 3. Даны координаты вершин треугольника АВС. Требуется найти: 1) длину стороны ВС; 2) уравнение линии ВС; 3) уравнение высоты, проведенной из точки А; 4) величину угла В; 5) проекцию вектора на вектор ; 6) систему неравенств, определяющих треугольник АВС. Сделать чертеж по координатам точек.

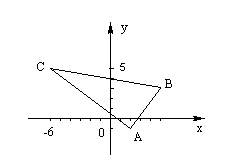
А(2; -1)

В (5; 3)

С(-6; 5)

1. Найдем координаты вектора

= (6 5; 5  3) = ( 11; 2).

Длина стороны ВС как длина вектора равна

.

2) Составим уравнение линии ВС, пользуясь каноническим уравнением прямой, М₀(х₀; у₀) = С(5; 3), .

, преобразуем его 2х  10 = 11у + 33,

2х + 11у  43 = 0 - уравнение прямой ВС.

3) Составим уравнение высоты АЕ, зная точку А(2; 1) и условие перпендикулярности прямой

,

у  у₀ = k(х  х₀) - уравнение прямой, проходящей через данную т. М₀(х₀; у₀) с угловым коэффициентом k.

у ( 1) = (х  2) или 2у + 2 = 11х  22,

11х  2у  24 = 0 - уравнение высоты АЕ.

4) Угол В образован векторами и , причем = (11; 2),

= (2  5; 1  3) = (3; 4),

,

 = В = arccos - острый.

5) Найдем проекцию на по формуле

, =(–8; 6), =(3; 4).

.

6) Находим уравнения сторон АВ и АС, используя каноническое уравнение.

АВ: А(2; 1); = (3; 4); ; 4х  8 = 3у + 3

или 4х  3у  11 = 0 уравнение прямой АВ.

АС: А(2; 1); = (8; 6); ; 6х  12 = 8у 8

или 3х + 4у  2 = 0 уравнение прямой АС.

Для того, чтобы определить область треугольника АВС, находим полуплоскость относительно каждой стороны АВС, подставляя в ее уравнение координаты соответствующей точки.

ВС: 2х + 11у  43 = 0, А (2; 1), имеем

22 + 11(1)  43 = 50 < 0;

АС: 3х + 4у  2 = 0, В (5; 3),

35 + 43  2 = 25 > 0;

АВ: 4х  3у  11 = 0, С (6; 5),

4 (  6)  35 11 = 50 < 0.

Система неравенств, определяющая треугольник АВС:

Задание 4. Найти пределы функции, не применяя правило Лопиталя.

а) = 2,

разделили числитель и знаменатель дроби на х² ,

, .

в) =

=

= = .

Умножили числитель и знаменатель дроби на сопряженный множитель , затем разложили на множители, сократили на (х  7).

с) =

= .

По формуле половинного аргумента преобразовали числитель и воспользовались формулой 1-го замечательного предела.

1, .

Задание 5. Найти данных функций:

а) . Находим производную частного функций:

=

= =

= .

в) у = (х + 1) arctg , находим производную произведения функций:

+ =

= arctg + (х + 1) = arctg + .

с) у = (х + ln sin х)³ .

Находим производную сложной функции у = f (u (x)), ,

= =

= 3  (x + ln sin x)²  (1 + ctg x).

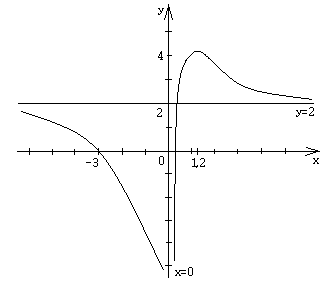
Задание 6. Исследовать функцию и построить ее график: .

1. Находим область определения функции D: (; 0)  (0; ).

2. Находим асимптоты графика:

При х = 0 функция не определена. Найдем односторонние пределы при х0:

и ,

следовательно, прямая х=0 – вертикальная асимптота.

у = kx + b – наклонная асимптота,

k= = = ,

числитель и знаменатель дроби разделили на х³.

= = ,

у = 2 - горизонтальная асимптота.

3) Точки пересечения с осями:

При у = 0 имеем или , отсюда

х₁ = 0,5; х₂ = 3.

4) Четность, нечетность:

f(x) = ,

f(  x) ≠ f(x) и f(  x) ≠  f(x), значит, функция f(x) не является ни четной, ни нечетной.

5) Возрастание, убывание, экстремумы:

;

у = 0, то 6  5х = 0, х = 1,2;

у = , х = 0  D;

х = 1,2 точка максимума и f_max = .

6) Выпуклость, вогнутость, точки перегиба.

,

у = 0, то 10х  18 = 0; х = 1,8

у = ; х = 0  D.

у

y

- точка перегиба графика функции.

График функции изображен на рисунке: