
- •1. Матрицы. Определители. Системы линейных уравнений
- •1.1. Матрицы. Действия с матрицами
- •1.2. Свойства действий с матрицами
- •1.3. Определители. Свойства определителей
- •1.4. Обратная матрица
- •1.5. Ранг матрицы
- •1.6. Системы линейных уравнений
- •1.7. Правило Крамера
- •1.8. Метод Гаусса
- •1.9. Теорема Кронекера-Капелли
- •2. Векторы на плоскости
- •2.1. Векторы, линейные операции над векторами
- •2.4. Скалярное произведение векторов, его свойства
- •3. Прямая линия на плоскости
- •4. Кривые второго порядка
- •5. Введение в анализ
- •5.1. Предел функции. Бесконечно малая и бесконечно большая функции
- •5.2. Теоремы о пределах
- •Постоянный множитель можно выносить за знак предела:
- •5.3. Раскрытие неопределенностей. Замечательные пределы
- •6. Производная и дифференциал
- •6.1. Производная функции
- •6.2. Производная сложной функции
- •6.3. Производные высших порядков
- •6.4. Дифференциалы функции
- •6.7. Выпуклость, вогнутость кривой. Точки перегиба
- •6.8. Асимптоты графика функции
- •6.9. Полная схема исследования функции
- •7. Задачи для контрольной работы
- •8. Образец выполнения контрольной работы
- •Из этой системы обратным ходом метода Гаусса находим
- •9. Вопросы для экзамена
- •Список литературы
- •Оглавление
- •1. Матрицы. Определители. Системы
- •1.1. Матрицы. Действия с матрицами 3
7. Задачи для контрольной работы
1 - 10. а) Упростить и вычислить;
б) выбрав матрицу А размером 3×3, найти обратную ей:
1.
 2.
2.

3.
 4.
4.

5.
 6.
6.

7.
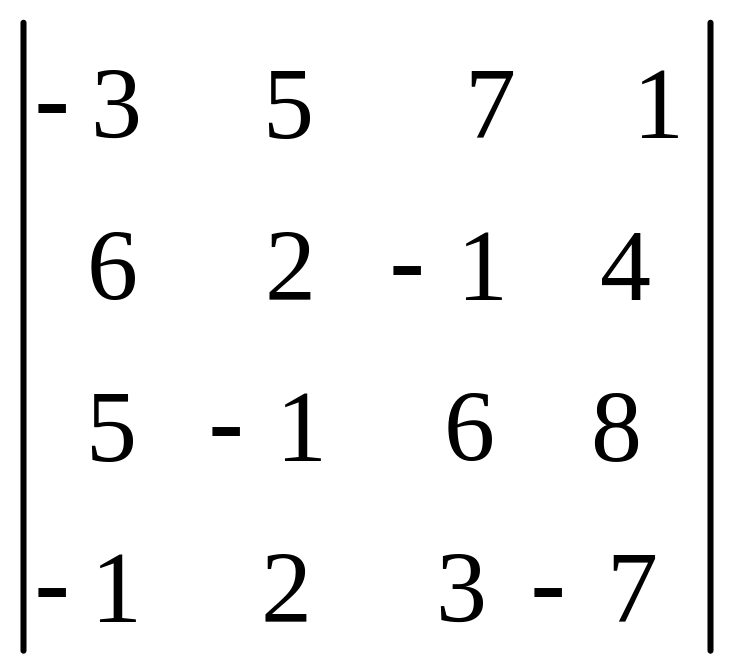 8.
8.

9.
 10.
10.
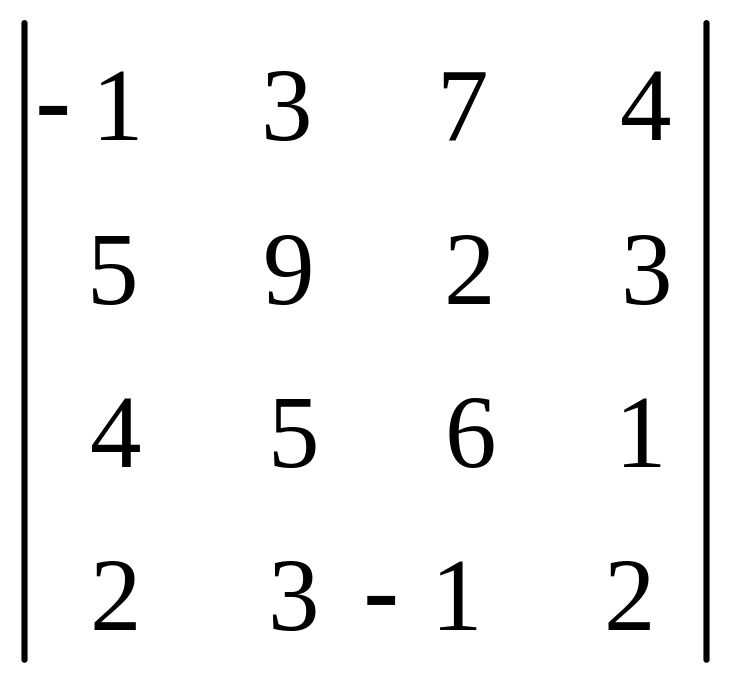 .
.
11 - 20. Решить систему методом Гаусса:
11.
 12.
12.

13.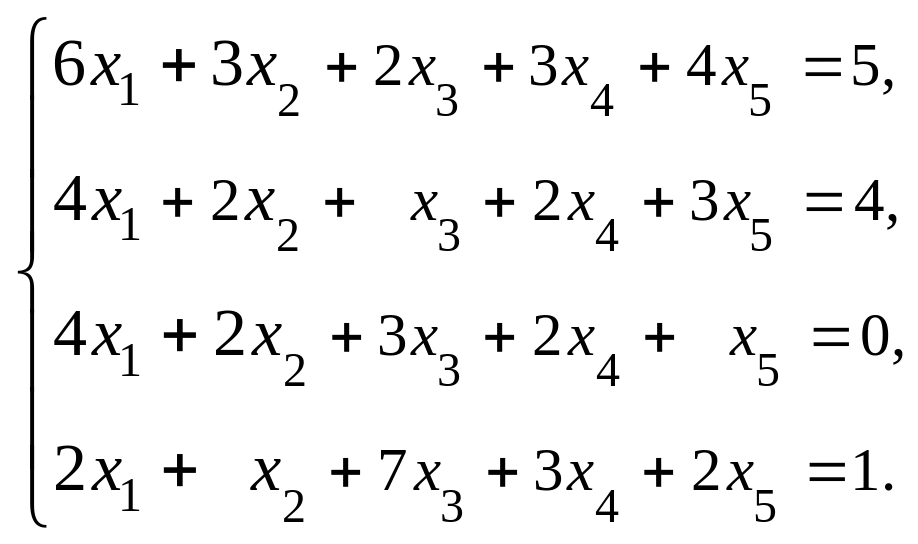 14.
14.
15.
 16.
16.

17.
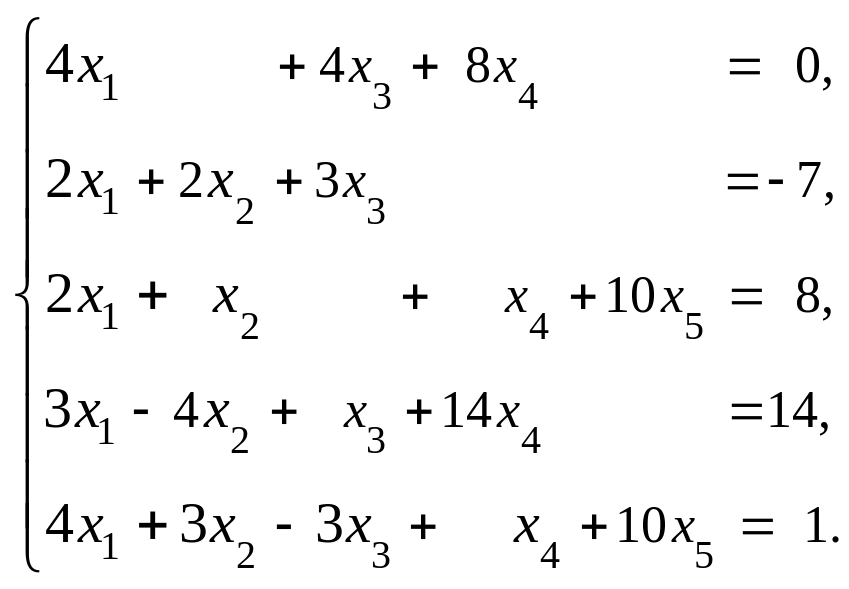 18.
18.

19.

20.

21 - 30. Даны координаты вершин треугольника АВС. Найти:
1) длину стороны ВС;
2) уравнение линии ВС;
3) уравнение высоты, проведенной из точки А;
4) величину угла В;
5) проекцию вектора
![]() на вектор
на вектор
![]() ;
;
6) систему неравенств, определяющую треугольник АВС.
Сделать чертеж по координатам точек.
21. А (10; -1); В (-3; 4); С (2; 4).
22. А (2; 6); В (4; 8); С (-2; 2).
23. А (1; 3); В (3; -4); С (-2; 8).
24. А (-2; -4); В (5; 7); С (0; 6).
25. А (10; 4); В (6; 8); С (-1; -4).
26. А (2; -8); В (7; 10); С (-3; -5).
27. А (9; 6); В (-1; -3); С (6; 10).
28. А (-10; -3); В (-2; -4); С (6; 7).
29. А (-8; -6); В (4; 5); С (1; 7).
30. А (-7; -2); В (5; 9); С (-3; 4).
31 - 40. Найти пределы функции, не применяя правило Лопиталя:
31. а)
![]() в)
в)
![]()
с)
![]()
32. а)
![]() в)
в)
![]()
с)
![]()
33. а)
![]() в)
в)
![]()
с)
![]()
34. а)
![]() в)
в)
![]()
с)
![]()
35. а)
![]() в)
в)
![]()
с)
![]()
36. а)
![]() в)
в)
![]()
с)
![]()
37. а)
![]() в)
в)
![]()
с)
![]()
38. а)
![]() в)
в)
![]()
с)
![]()
39. а)
![]() в)
в)
![]()
с)
![]()
40. а)
![]() в)
в)
![]()
с)

41 - 50. Найти производные данных функций:
41. а)
![]() в)
в)
![]()
с)
![]()
42. а)
![]() в)
в)
![]()
с)
![]()
43. а)
![]()
в)
![]() с)
с)
![]()
44. а)
![]() в)
в)
![]()
с)
![]()
45. а)
![]() в)
в)
![]()
с)
![]()
46. а)
![]() в)
в)
![]()
с)
![]()
47. а)
![]() в)
в)
![]()
с)
![]()
48. а)
![]() в)
в)
![]()
с)
![]()
49. а)
![]() в)
в)
![]()
с)
![]()
50. а)
![]() в)
в)
![]()
с)
![]()
51 - 60. Исследовать функцию и построить ее график:
51.
![]() 52.
52.
![]()
53.
![]() 54.
54.
![]()
55.
![]() 56.
56.
![]()
57.
![]() 58.
58.
![]()
59.
![]() 60.
60.
![]()
8. Образец выполнения контрольной работы
Задание 1. а) Упростить и вычислить

![]() =
56
+ 36 = 20.
=
56
+ 36 = 20.
Используя свойства определителей преобразуем данный определитель так, чтобы три элемента некоторого ряда равнялись нулю. Для этого выберем 3-ю строку, в которой есть 0, затем 1-й столбец сложим со 2-м, далее 1-й столбец умножим на (2) и сложим с 4-м. Вычисляем определитель, разлагая его по 3-й строке. Получим определитель 3-го порядка, который разлагаем по 1-й строке, обнулив предварительно два элемента. Для этого 2-й столбец умножим на 2 и сложим с 1-м столбцом, 2-й столбец умножим на (1) и сложим с 3-м столбцом.
б) Выбрав матрицу А размером 3×3 найти обратную ей.
Возьмем первые три строки и три столбца в данном определителе.
 .
.
Вычислим определитель матрицы А, разлагая по 1-й строке.

![]() =
=
= 3 + 3(1) = 7 ≠ 0,
матрица невырожденная.
Вычислим алгебраические дополнения
![]() = 3;
= 3; ![]() = 1;
= 1;
![]() = 3;
= 3; ![]() = 1;
= 1;
![]() = 1;
= 1; ![]() =
2;
=
2;
![]() =
2;
=
2; ![]() = 5;
= 5;
![]() = 3.
= 3.
Обратная матрица примет вид
 .
.
Задание 2. Решить систему методом Гаусса:

Умножим 1-е уравнение на (4) и прибавим ко 2-му, 1-е на (3) и прибавим к 3-му, 1-е на (2) и прибавим к 4-му, получим
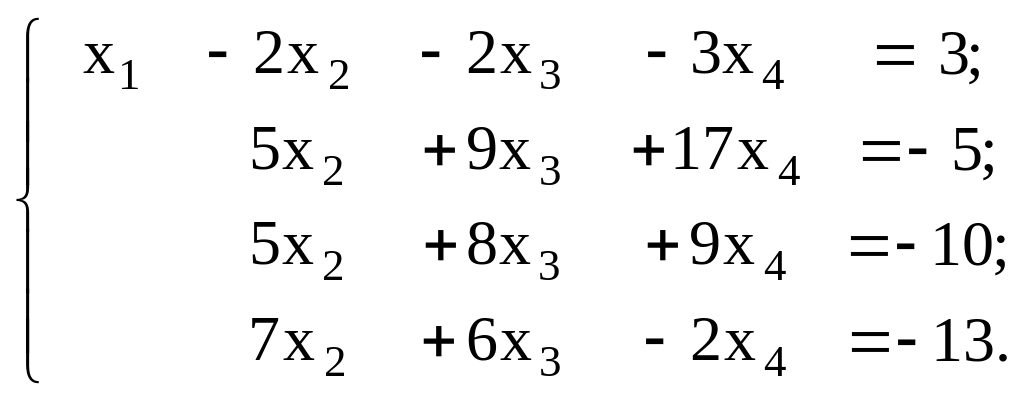
Затем умножим 2-е уравнение на (1) и прибавим к 3-му, умножим 2-е уравнение на 7, а 4-е уравнение умножим на (5) и сложим.
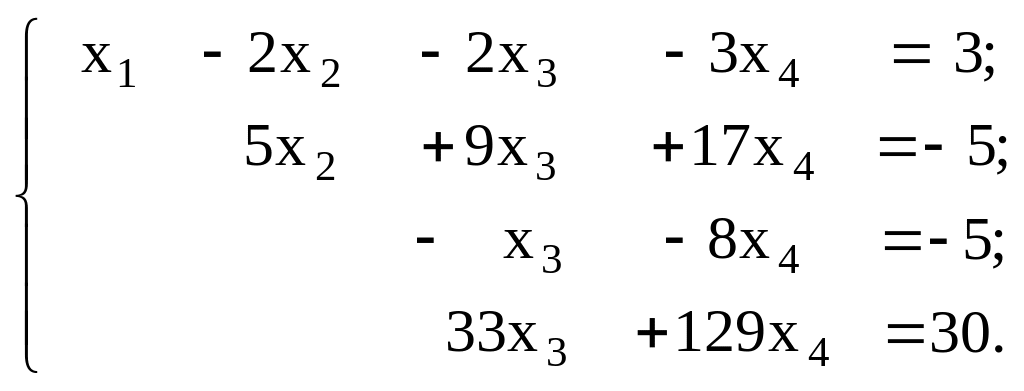
Умножим 3-е уравнение на 33 и прибавим к 4-му.

