
- •(Л4) Тема 2.2: Уравнение линии на плоскости. Кривые второго порядка.
- •1 Уравнение прямой линии с угловым коэффициентом
- •2 Уравнение прямой, проходящей через данную точку в данном направлении
- •3 Уравнение прямой, проходящей через две данные точки
- •4 Угол между двумя прямыми
- •5 Условия параллельности и перпендикулярности двух прямых
- •6 Общее уравнение прямой
- •7 Взаимное расположение двух прямых на плоскости
- •8 Расстояние от точки до прямой
- •9 Кривые второго порядка (рассматривается студентами самостоятельно)
- •Конспект лекций по высшей математике: полный курс. Письменный д.Т.4-е изд. — м.: Айрис-пресс, 2006. — 608 с.
7 Взаимное расположение двух прямых на плоскости
Если две прямые l1 и l2 лежат на плоскости, то возможны три различных случая их взаимного расположения: 1)пересекаются (т.е. имеют одну общую точку); 2) параллельны и не совпадают; 3) совпадают.
Выясним, как узнать, какой из этих случаев имеет место, если эти прямые заданы своими уравнениями в общем виде:
![]() (12)
(12)
Если прямые l1 и l2 пересекаются в некоторой точке М(х,у), то координаты этой точки должны удовлетворять обоим уравнениям системы (12).
Следовательно, чтобы найти координаты точки пересечения прямых l1 и l2, надо решить систему уравнений (12):
1) если система (12) имеет единственное решение, то прямые l1 и l2 пересекаются;
2) если система (12) не имеет решения, то прямые l1 и l2 параллельны;
3) если система (12) имеет множество решений, то прямые l1 и l2 совпадают.
Условием совпадения двух прямых является пропорциональность соответствующих коэффициентов их уравнений.
Пример 10. Пересекаются ли прямые 3х+4у-1=0 и 2х+3у-1=0 ?
Решение: Решим систему уравнений:

система имеет единственное решение, следовательно прямые пересекаются. Точка пересечения прямых имеет координаты (-1;1).
Пример 11. Параллельны, ли прямые 2х-у+2=0 и 4х-2у-1=0?
Решение: Решим систему
уравнений 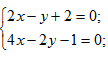
Эта система не имеет решений, следовательно прямые параллельны.
Пример 12. Совпадают ли прямые х+у+1=0 и 3х+3у+3=0?
Решение: Совпадают, так как коэффициенты пропорциональны.
Пример 13. Составить уравнение прямой линии, проходящей через точку пересечения прямых х+у-1=0, х-у+2=0 и через точку (2,1).
Решение: Находим координаты
точки пересечения двух данных прямых
линий. Для этого решаем данные уравнения
совместно. Складывая, находим: 2х+1=0,
откуда ![]()
Вычитая из первого уравнения
второе, получаем: 2у-3=0, откуда ![]() .
Далее, остается составить уравнение
прямой линии по двум точками (
.
Далее, остается составить уравнение
прямой линии по двум точками (![]() )
и (2;1)
)
и (2;1)
Искомое уравнение будет 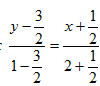 ,
или
,
или  или
или 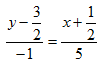 откуда
откуда ![]() или
x+5y-7=0
или
x+5y-7=0
8 Расстояние от точки до прямой
Расстояние d от точки M0(x0,y0,z0)до прямой Аx+By+C=0 вычисляется по формуле:
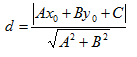 (13)
(13)
9 Кривые второго порядка (рассматривается студентами самостоятельно)
Вопросы для самоконтроля.
1 Запишите формулы:
Уравнение прямой линии с угловым коэффициентом
Уравнение прямой, проходящей через данную точку в данном направлении
Уравнение прямой, проходящей через две данные точки
Угол между двумя прямыми
Условия параллельности и перпендикулярности двух прямых
Общее уравнение прямой
Расстояние от точки до прямой
Использованная литература.
Конспект лекций по высшей математике: полный курс. Письменный д.Т.4-е изд. — м.: Айрис-пресс, 2006. — 608 с.
