(Л3) Тема 2.1: Системы координат на прямой, плоскости и в пространстве. Скалярное, векторное и смешанное произведения векторов.

Актуальность темы (мотивация изучения).  Знание фундаментальных основ аналитической геометрии способствует формированию специализированных знаний, соединяющих профессиональные знания и умения узких специалистов и широкие общенаучные фундаментальные знания. Геометрический анализ экономических задач представляет общий научный интерес.

Цель лекции: Обучение студентов основным понятиям аналитической геометрии

План лекции:

1. Декартова прямоугольная система координат на плоскости 

2. Расстояние между двумя точками на плоскости 

3. Деление отрезка в данном отношении 

4. Вычисление площади треугольника 

5. Векторы и линейные операции над векторами 

6. Скалярное произведение векторов и его свойства 

7. Векторное, смешанное произведение векторов и их свойства

1Декартова прямоугольная система координат на плоскости

Возьмем на плоскости две взаимно перпендикулярные прямые – две оси координат Ох и Оу с указанными на них положительными направлениями (рис.1). Прямые Ох и Оу называются координатными осями, точка их пересечения О – началом координат.

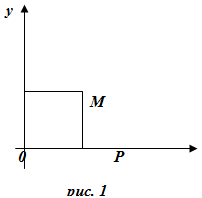
Координатные оси Ох, Оу с выбранной единицей масштаба называются декартовой прямоугольной (или прямоугольной) системой координат на плоскости.

Произвольной точке М плоскости поставим в соответствие два числа:  абсциссу х, равную расстоянию от точки М до оси Оу, взятому со знаком «+», если М лежит правее Оу, и со знаком «-» ,если М лежит левее Оу; ординату у, равную расстоянию от точки М до оси Ох, взятому со знаком «+», если М лежит выше Ох, и со знаком «-», если М лежит ниже Ох. Абсцисса х и ордината у называются декартовыми прямоугольными координатами точки М(х;у).

Начало координат имеет координаты (0;0).  Оси координат делят плоскость на четыре части, называемые четвертями или квадрантами (иногда их также называют координатными углами). Часть плоскости, заключенная между положительными полуосями Oх и Oу, называется первым квадрантом. Дальше нумерация квадрантов идет против часовой стрелки (рис. 2). Для всех точек I квадранта х>0, у>0; для точек I I квадранта х<0, у>0, в I I I квадранте х<0, у<0 и в IV квадранте х>0, у<0.

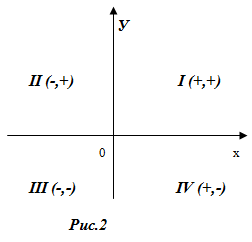
2 Расстояние между двумя точками на плоскости

Расстояние между двумя данными точками равно корню квадратному из суммы квадратов разностей одноименных координат этих точек.

Пример 1. Найти расстояние между точками (-1;4) и (2;0).

Решение: Искомое расстояние вычисляется по формуле (1). Здесь x₁=-1, y₁=4, x₂=2, y₂=0.

Следовательно, 

3 Деление отрезка в данном отношении

Пусть даны точки A(x₁;y₁)  и B(x₂;y₂).

Координаты точки М(х,у), лежащей на отрезке АВ и делящей его в данном отношении:

вычисляются по формулам:

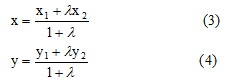
В частности, при   получаются формулы для координат середины отрезка:

Пример 2. Известны точки A(-2;5), B(4;17)- концы отрезка [AB]. На этом отрезке находится точка М, расстояние которой от А в два раза больше расстояния от В. Определить координаты точки М.

Решение.

Так как |AM|=2|MB|, то  .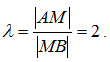 

Здесь x₁=-2, y₁=5, x₂=4, y₂=17; следовательно,   то есть M(2;13).

Пример 3. Точка M(2;3) служит серединой отрезка [AB]. Определить координаты точки А, если B(7;5).

Решение. Здесь x=2, y=3, x₂=7, y₂=5, откуда

то есть A(-3;1)