Проверка необходимых и достаточных условий экстремума для найденной точки минимума
Для проверки необходимого условия существования экстремума функции найдем первую производную Zpr(x,y) от целевой функции Z(x,y) и подставим получившиеся координаты точек x и y. Производная равна нулю (учитывая допустимую погрешность), следовательно, необходимое условие существования экстремума выполнено.
А для проверки достаточного условия нужно построить матрицу Гессе и с помощью встроенной функции в Mathcad найти её определитель, подставив координаты полученной точки.
Реализуем алгоритм проверки необходимого условия в Mathcad. Листинг программы представлен на рисунке 8.
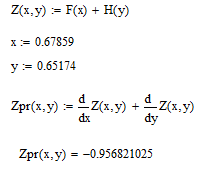
Рисунок 8 – Листинг программы по проверке необходимого условия
Реализуем программу для проверки достаточного условия. Листинг программы представлен на рисунке 9.
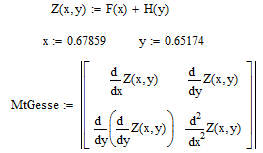
Рисунок 9 – Листинг программы по проверке достаточного условия
По выполненной программе на рисунке 9 можно сделать вывод, что матрица Гессе положительно определена, это означает то что мы нашли точку минимума.
Разработки программы проверки ограничений
Для проверки ограничений оптимизационной задачи рассмотренной в курсовой работе, мной была разработана программа. Функция программы названа Proverka. Программа заключается в том что, мы задаем два условия: если значение точки x попадает в промежуток от Ax до By и если значение y попадает в промежуток от Ay и By, которые должны быть верными и перемножаем их, в итоге программа должна выдать значение 1 (истина). На листинге программе приведенной на рисунке 9, мы видим, что найденная точка попадает в область допустимых значений.
Рисунок 9 – Листинг программы проверки ограничений
Заключение
В курсовой работе был рассмотрен градиентный метод оптимизации с равномерным поиском. Составлена программа в Mathcad, реализующая этот метод. Была найдена точка оптимума, являющаяся минимумом Z(x,y)=5.7332. В ней выполняются необходимые и достаточные условия.
Градиентный метод является эффективным. Однако могут возникнуть трудности с вычислением и исследованием матрицы вторых производных (матрицы Гессе).
Список литературных источников
Сыроежкин Е.В. Методические указания по дисциплине «Методы оптимизации в управлении». – Москва, 2012 – 30с.
Жилинскас А., Шалтянис В. Поиск оптимума: компьютер расширяет
возможности.- М.: Наука, 1989.- 128 с
Химмельблау Д. Прикладное нелинейное программирование.- М.: Мир, 1975. -534 с.