Згідно теореми Лежандра, значення кутів плоского (лежандрового) трикутника буде

(3.7)

Сферичний надлишок можна обчислити, наприклад, за формулами (3.4).

Отже, якщо у сферичному трикутнику відома вихідна сторона, наприклад, і сферичні кути (див. рис.3.3), то за першою формулою (3.4) обчислюємо сферичний надлишок трикутника і знаходимо плоскі кути . Потім розв’язуємо трикутник за стороною та знайденими плоскими кутами, застосовуючи формули плоскої тригонометрії (теорему синусів), тобто

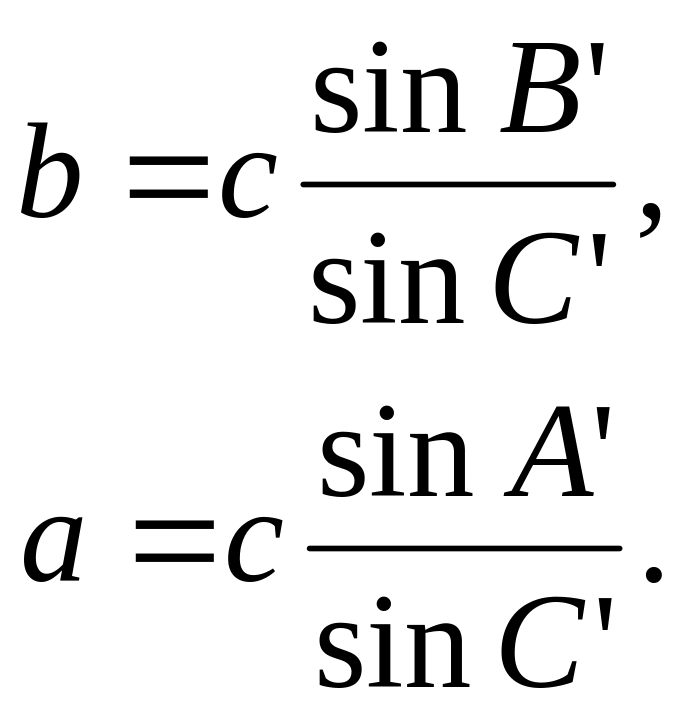(3.8)

Точність розв'язування сферичних трикутників, які можна розв’язувати за теоремою Лежандра, залежить не тільки від розмірів сторін, але і від форми трикутника. Аналізом формул встановлено, що допустимі розміри сторін трикутника знаходяться в межах від 75 до 150 км.

В) за способом аддитаментів

У попередньому способі для застосування формул плоскої тригонометрії вводилися поправки за сферичність у кути.

Можливим є також спосіб використання сферичних кутів, але з введенням поправок в сторони трикутника. Розглянемо даний спосіб.

Із сферичного трикутника (рис.3.3) за теоремою синусів маємо

(3.9)

де - відома сторона, - шукана сторона даного сферичного трикутника.

Поскільки сторони сферичного трикутника є малими в порівнянні з радіусом сфери , то їх тригонометричні функції розкладемо в ряд, обмежуючись членами третього порядку:

Позначивши

і, крім того

напишемо

Або остаточно

(3.10)

і, аналогічно, для другої сторони

. (3.11)

З цих формул видно, що головні члени представляють собою розв'язування сферичного трикутника як плоского, причому кути в них є сферичними. Поправочні члени називають аддитаментами. Тому і розв'язування сферичного трикутника за формулами (3.10), (3.11) називають способом аддитаментів. Строго кажучи, аддитаментами називалися малі поправки до логарифму головного члена, коли формули виводились із застосуванням логарифмів. Хоча логарифмічні методи втратили своє значення і на практиці не застосовуються, проте в назвах окремих способів, і в тому числі при розв’язуванні сферичних трикутників, збереглися первісні терміни.

Отже, якщо від вихідної сторони відняти її аддитамент і розв’язати трикутник зі сферичними кутами за формулами плоскої тригонометрії, то, додавши до знайдених довжин сторін їхні аддитаменти, отримаємо довжини сторін сферичного трикутника.

Точність розв’язування малих сферичних трикутників способом аддитаментів є аналогічною, як і для розв’язування їх за теоремою Лежандра.

Г) за виміряними сторонами

У випадку, коли в геодезичній мережі вимірюються лише сторони трикутників, виникає потреба обчислення горизонтальних кутів, які в подальшому можуть мати окреме застосування, наприклад, для передачі геодезичного азимута від однієї сторони до іншої.

Порядок обчислень при цьому буде наступний. Виміряні між пунктами прямолінійні відстані редукують на поверхню еліпсоїда, згідно теорії редукцій геодезичних вимірювань з фізичної поверхні Землі на поверхню еліпсоїда.

За знайденими таким чином сторонами сферичного трикутника обчислюють плоскі кути (див. рис.3.3), використовуючи наступні формули плоскої тригонометрії:

Якщо довжини сторін не перевищують 100 км, то достатньо обчислити сферичний надлишок за формулами (3.2), а потім одну третину його додати до кожного плоского кута згідно формули (3.7).